目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
基于有序模式的度量(Ordinal Pattern-based Measures)是一种用于多变量时间序列非线性分析的方法。它可以通过分析时间序列中的有序模式来获取关于序列动力学和非线性性质的信息。以下是基于有序模式的度量方法的一般研究步骤:
1. 多变量时间序列选择:选择你感兴趣的多变量时间序列数据。这些数据可以代表各种应用领域中的观测变量,例如金融数据、天气数据或生物学数据等。
2. 计算有序模式:将多变量时间序列数据转换为有序模式序列。有序模式是基于变量之间的相对大小关系而形成的序列。这可以通过将原始时间序列中的每个数据点与其他数据点进行比较来实现。
3. 确定有序模式:对于给定的模式长度(pattern length),确定所有可能的有序模式。模式长度是在指定的时间窗口内对变量进行比较的步骤数量。
4. 计算模式频率:计算每个有序模式的频率或出现次数。这可以通过扫描整个有序模式序列并对每个模式进行计数来实现。
5. 模式度量计算:基于模式频率,计算一系列模式度量来描述时间序列的非线性性质。一些常见的模式度量包括熵、复杂度、不规则度等。这些度量可以量化时间序列的复杂性和规律性。
6. 统计分析:对模式度量进行统计分析,以获取关于时间序列非线性性质的信息。这可以包括计算平均值、标准差、相关性等统计指标,以及使用假设检验方法来评估时间序列之间的差异。
7. 结果解释:解释和解读分析结果,以洞察时间序列的非线性动力学和相关特性。这可能需要与领域专家结合,将模式度量结果与问题域的理论知识进行关联。
需要注意的是,基于有序模式的度量方法在时间序列非线性分析中是一种较新的方法,需要对相关理论和算法进行深入了解。此外,选择合适的模式长度、模式度量和统计分析方法等也需要针对具体问题进行权衡和调整。
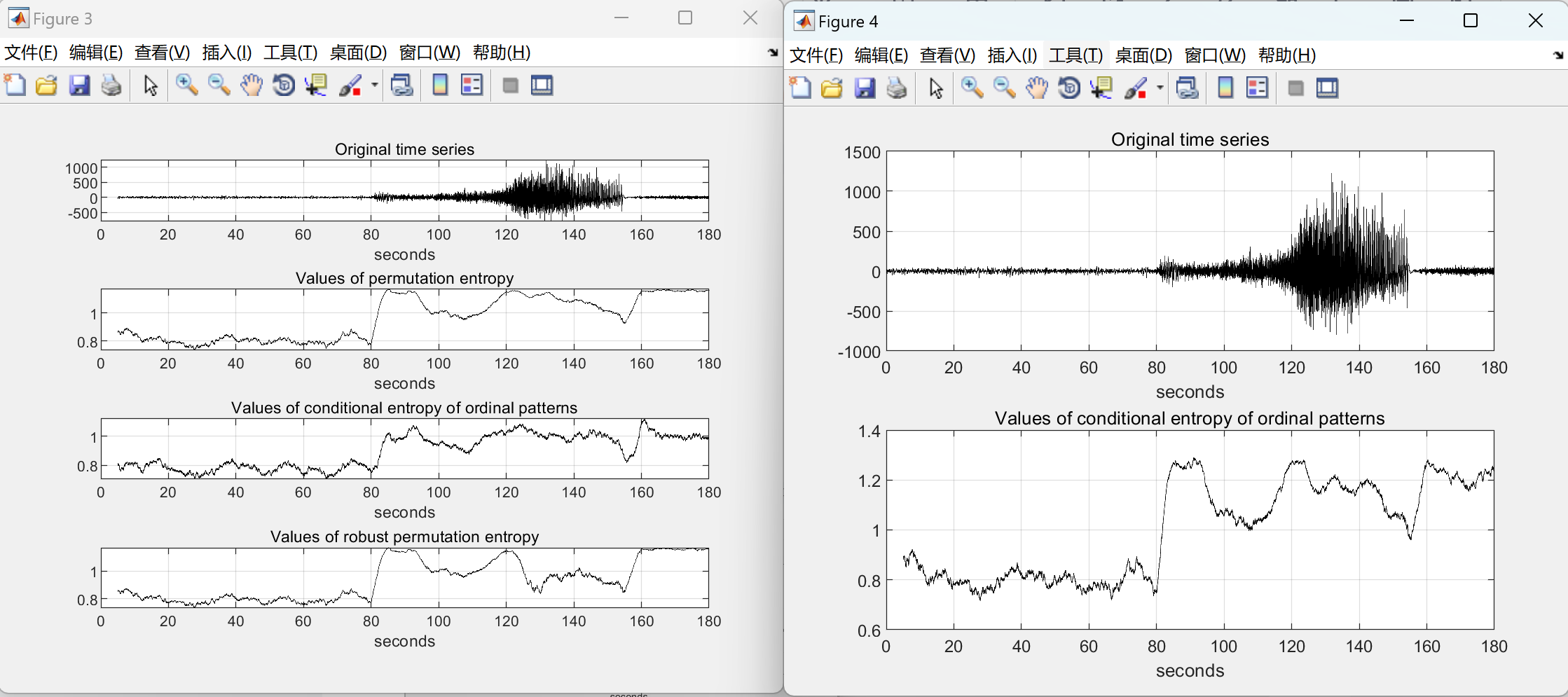
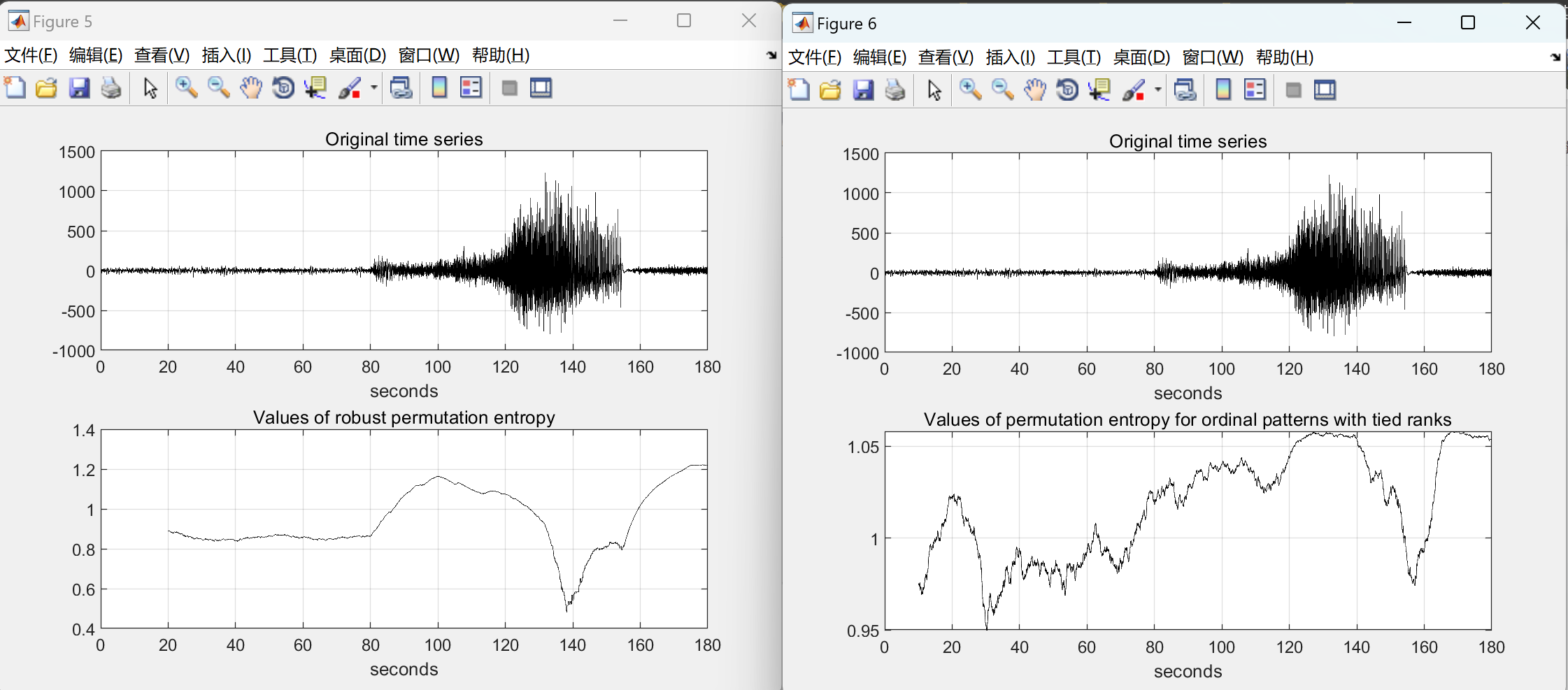
📚2 运行结果



部分代码:
%% compute permutation entropy in sliding windows
load( 'tonicClonic.mat' );
cfg = [];
cfg.method = 'PE'; % compute permutation entropy
cfg.order = 3; % ordinal pattens of order 3 (4-points ordinal patterns)
cfg.delay = 2; % delay 2 between points in ordinal patterns
% (one point between successive points in ordinal patterns)
cfg.windowSize = 512; % window size = 512 time steps
cfg.time = 0:1/102.4:179.999; % OPTIONAL time axis for plotting
cfg.units = 'seconds'; % OPTIONAL units of time for plotting
outdata = OPanalysis( cfg, indata );
%% compute permutation entropy and ordinal distributions in sliding windows
load( 'tonicClonic.mat' );
cfg = [];
cfg.method = 'opdPE'; % compute permutation entropy
cfg.order = 3; % ordinal pattens of order 3 (4-points ordinal patterns)
cfg.orderSeq = 6; % ordinal pattens of order 6 for plotting their sequence (7-points ordinal patterns)
cfg.delay = 1; % delay 1 between points in ordinal patterns (successive points)
cfg.windowSize = 1024; % window size = 1024 time steps
cfg.time = 0:1/102.4:179.999; % OPTIONAL time axis for plotting
cfg.units = 'seconds'; % OPTIONAL units of time for plotting
outdata = OPanalysis( cfg, indata );
%% compute all the implemented measures simultaneously for comparison
load( 'tonicClonic.mat' );
cfg = [];
cfg.method = 'all'; % compute all implemented ordinal-patterns-based measures
cfg.order = 4; % ordinal patterns of order 4 (5-points ordinal patterns)
cfg.delay = 1; % delay 1 between points in ordinal patterns
cfg.windowSize = 512; % window size = 512 time steps
cfg.lowerThreshold = 0.2; % the distance considered negligible between points
cfg.upperThreshold = 200; % the distance between points most probably related to artifact
cfg.time = 0:1/102.4:179.999; % OPTIONAL time axis for plotting
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1] Amigo, J.M., Keller, K. and Unakafova, V.A., 2015. On entropy, entropy-like quantities, and applications. Discrete & Continuous Dynamical Systems-Series B, 20(10).
[2] Bandt C., Pompe B., Permutation entropy: a natural complexity measure for time series. Physical review letters, 2002, APS
[3] Keller, K., and M. Sinn. Ordinal analysis of time series. Physica A: Statistical Mechanics and its Applications 356.1 (2005): 114--120
[4] Keller, K., Unakafov, A.M. and Unakafova, V.A., 2014. Ordinal patterns, entropy, and EEG. Entropy, 16(12), pp.6212-6239.
[5] Zanin, M., Zunino, L., Rosso, O.A. and Papo, D., 2012.
Permutation entropy and its main biomedical and econophysics applications: a review. Entropy, 14(8), pp.1553-1577.
[6] Unakafova, V.A., Keller, K., 2013. Efficiently measuring complexity on the basis of real-world Data. Entropy, 15(10), 4392-4415.
[7] Unakafova, V.A., 2015. Investigating measures of complexity for dynamical systems and for time series (Doctoral dissertation, University of Luebeck).
[8] Bian, C., Qin, C., Ma, Q.D. and Shen, Q., 2012. Modified permutation-entropy analysis of heartbeat dynamics. Physical Review E, 85(2), p.021906.
[9] Amigo, J.M., Zambrano, S. and Sanjuan, M.A., 2008. Combinatorial detection of determinism in noisy time series. EPL (Europhysics Letters), 83(6), p.60005.
[10] Cao, Y., Tung, W.W., Gao, J.B. et al., 2004. Detecting dynamical changes in time series using the permutation entropy. Physical Review E, 70(4), p.046217.
[11] Riedl, M., Muller, A. and Wessel, N., 2013. Practical considerations of permutation entropy. The European Physical Journal Special Topics, 222(2), pp.249-262.