文章目录
- 区间问题
- 905. 区间选点
- 908. 最大不相交区间数量
- 906. 区间分组
- 907. 区间覆盖
- Huffman树
- 148. 合并果子
- 排序不等式
- 913. 排队打水
- 绝对值不等式
- 104. 货仓选址
- 推公式
- 125. 耍杂技的牛
6.18~7.22完成算法基础的学习,剩下时间用来暴刷《算法竞赛指南》以巩固基础
区间问题
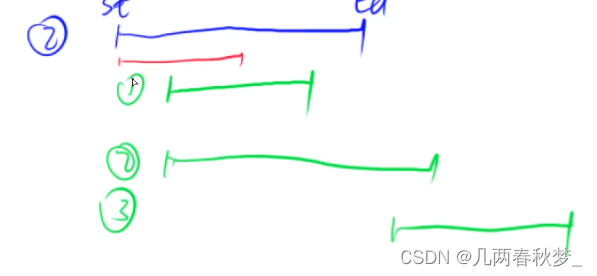
905. 区间选点
905. 区间选点 - AcWing题库
选择尽可能少的点,使得每一个区间都包含一个点
将所有区间按照右端点排序,每次选择右端点,这样当前区间就包含了一个点
由于之后的区间右端点都是大于等于当前区间右端点的,所以只要后续区间与当前区间相交,那么当前区间的右端点也被后续区间包含
若后续区间与当前区间互不相交,那么选择该区间的右端点
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
struct range
{
int l ,r;
bool operator<(const range& x)
{
return r < x.r;
}
}ranges[N];
int main()
{
int n;
scanf("%d", &n);
for (int i = 0; i < n; ++ i) scanf("%d%d", &ranges[i].l, &ranges[i].r);
sort(ranges, ranges + n);
int res = 0, r = -2e9;
for (int i = 0; i < n; ++ i )
{
if (ranges[i].l > r)
{
r = ranges[i].r;
res ++ ;
}
}
printf("%d\n", res);
return 0;
}
908. 最大不相交区间数量
908. 最大不相交区间数量 - AcWing题库

求出给定区间中,最多的互不相交区间数量
将所有区间按照右端点升序排序,遍历所有区间
记互不相交的区间中右端点的最大值为mr
- 若当前区间的左端点大于mr,那么当前区间与所有互不相交的区间互不相交,将其加入互不相交区间,更新mr
- 若当前区间的左端点小于mr,那么当前区间与互不相交的区间中某个区间相交
为什么该贪心策略能选择最多的互不相交区间?所有的区间按照右端点排序,每次选择一个区间,使之与已经选择的互不相交区间不相交。同时该区间的右端点最小,说明之后能选择的区间数量最多
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
struct range
{
int l, r;
bool operator<(const range& x)
{
return r < x.r;
}
}ranges[N];
int main()
{
int n;
scanf("%d", &n);
for (int i = 0; i < n; ++ i ) scanf("%d%d", &ranges[i].l, &ranges[i].r);
sort(ranges, ranges + n);
int mr = -2e9, res = 0;
for (int i = 0; i < n; ++ i )
{
if (ranges[i].l > mr)
{
res ++ ;
mr = ranges[i].r;
}
}
printf("%d\n", res);
return 0;
}
906. 区间分组
906. 区间分组 - AcWing题库
将所有的区间分组,使得每一组的区间互不相交,并且分的组尽可能少
将所有区间按左端点排序,用小堆维护所有组的右端点最大值,使得堆顶是这些最大值的最小值
- 若当前区间的左端点大于堆顶,说明当前区间可以加入所有组中,右端点最大值最小的一组,加入后用当前区间的右端点更新该组右端点最大值
- 若当前区间的左端点小于等于堆顶,说明所有组中都存在一个区间 [ l , r ] [l, r] [l,r],l小于等于左端点并且r大于等于左端点。即区间重叠产生了冲突,当前区间无法加入任意一组区间,只能将当前区间放入一个新的组
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 1e5 + 10;
struct range
{
int l, r;
bool operator<(const range& x)
{
return l < x.l;
}
}ranges[N];
int main()
{
int n;
scanf("%d", &n);
for (int i = 0; i < n; ++ i ) scanf("%d%d", &ranges[i].l, &ranges[i].r);
sort(ranges, ranges + n);
priority_queue<int, vector<int>, greater<int>> q;
for (int i = 0; i < n; ++ i )
{
if (q.empty() || ranges[i].l <= q.top()) // 开新组
q.push(ranges[i].r);
else
{
q.pop();
q.push(ranges[i].r);
}
}
printf("%d\n", q.size());
return 0;
}
907. 区间覆盖
907. 区间覆盖 - AcWing题库
给定区间
[
s
,
t
]
[s, t]
[s,t],用最少的区间覆盖给定区间
将所有区间按照左端点排序
- 对于所有左端点小于等于s的区间,选择右端点最大的区间
- 用该区间的右端点更新s,即 s = r s=r s=r
重复以上两个步骤,直到
s
>
=
t
s >= t
s>=t,此时
[
s
,
t
]
[s, t]
[s,t]区间被完全覆盖,所以重复次数就是需要的最少区间数量
其中有两个无解的情况:
- 对于所有左端点小于等于s的区间,最大的右端点小于等于s
- 所有的区间更新完, s < t s < t s<t
若遇到第一种情况直接退出更新,否则可能陷入死循环
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
struct range
{
int l, r;
bool operator<(const range& x)
{
return l < x.l;
}
}ranges[N];
int main()
{
int s, t, n;
scanf("%d%d%d", &s, &t, &n);
for (int i = 0; i < n; ++ i ) scanf("%d%d", &ranges[i].l, &ranges[i].r);
sort(ranges, ranges + n);
int i = 0, r = -2e9, res = 0;
bool flag = false;
while (i < n)
{
while (i < n && ranges[i].l <= s)
{
r = max(r, ranges[i].r);
i ++ ;
}
if (r <= s && s != t) break;
s = r;
res ++ ;
if (s >= t)
{
flag = true;
break;
}
}
if (flag) printf("%d\n", res);
else puts("-1");
return 0;
}
debug:给定区间的s和t可能相等,此时右端点最大值被更新成s时不能直接break,所以这里要特判一下:if (r <= s && s != t) break;
Huffman树
148. 合并果子
148. 合并果子 - AcWing题库
经典Huffman问题,节点权值与根节点的距离具有负相关性,权值越大的节点离根节点的距离越近,权值越小的节点离根节点的距离越远,此时合并果子消耗的体力最小
所有叶子节点乘以其到根节点的距离累加,为消耗的总体力值
#include <iostream>
#include <queue>
using namespace std;
priority_queue<int, vector<int>, greater<int>> q;
int main()
{
int n, x;
scanf("%d", &n);
for (int i = 0; i < n; ++ i )
{
scanf("%d", &x);
q.push(x);
}
int res = 0;
while (q.size() > 1)
{
int a = q.top(); q.pop();
int b = q.top(); q.pop();
res += a + b;
q.push(a + b);
}
printf("%d\n", res);
return 0;
}
排序不等式
913. 排队打水
913. 排队打水 - AcWing题库
打水时间短的人排在前面,长的人排在后面,这样总时间最小
因为第i个人打水,后面n-i个人都要等待他打水结束,有等式:
t
1
(
n
−
1
)
+
t
2
∗
(
n
−
2
)
+
.
.
.
+
t
i
(
n
−
(
n
−
1
)
)
t_1(n-1)+t_2*(n-2)+...+t_i(n-(n-1))
t1(n−1)+t2∗(n−2)+...+ti(n−(n−1))
前面的数乘以的数较大,后续的数乘以的数较小,t乘以的数从大到小,要使得结果最小,就要使t从小到大
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
int a[N];
int main()
{
int n;
scanf("%d", &n);
for (int i = 0; i < n; ++ i ) scanf("%d", &a[i]);
sort(a, a + n);
long long res = 0;
for (int i = 0; i < n - 1; ++ i )
res += a[i] * (n - 1 - i);
printf("%lld\n", res);
return 0;
}
绝对值不等式
104. 货仓选址
104. 货仓选址 - AcWing题库

绝对值不等式:
∣
x
−
a
∣
+
∣
x
−
b
∣
>
=
∣
a
−
b
∣
|x-a|+|x-b|>=|a-b|
∣x−a∣+∣x−b∣>=∣a−b∣
在x建立一个货仓,使得它离其他商店最近,需要使式子最小:
∣
x
1
−
x
∣
+
∣
x
2
−
x
∣
+
.
.
.
+
∣
x
n
−
1
−
x
∣
+
∣
x
n
−
x
∣
|x_1-x|+|x_2-x|+...+|x_{n-1}-x|+|x_n-x|
∣x1−x∣+∣x2−x∣+...+∣xn−1−x∣+∣xn−x∣
将首尾两个式子看成一组:
(
∣
x
1
−
x
∣
+
∣
x
n
−
x
∣
)
+
.
.
.
+
(
∣
x
2
−
x
∣
+
∣
x
n
−
1
−
x
∣
)
(
1
)
(|x_1-x|+|x_n-x|)+...+(|x_2-x|+|x_{n-1}-x|)\ (1)
(∣x1−x∣+∣xn−x∣)+...+(∣x2−x∣+∣xn−1−x∣) (1)
由绝对值不等式有:
∣
x
n
−
x
1
∣
+
.
.
.
+
∣
x
n
−
1
−
x
2
∣
(
2
)
|x_n-x_1|+...+|x_{n-1}-x_2|\ (2)
∣xn−x1∣+...+∣xn−1−x2∣ (2)
(2)式为(1)式的最小值

要让等号成立,就要让x在两数之间
若n为奇数,那么x等于中位数。若n为偶数,那么x在中间两个数(包含两个数)之间就行
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
int a[N];
int main()
{
int n;
scanf("%d", &n);
for (int i = 0; i < n; ++ i ) scanf("%d", &a[i]);
sort(a, a + n);
int res = 0;
for (int i = 0; i < n; ++ i ) res += abs(a[i] - a[n / 2]);
printf("%d\n", res);
return 0;
}
推公式
125. 耍杂技的牛
125. 耍杂技的牛 - AcWing题库

以 ( w i + s i ) (w_i + s_i) (wi+si)为关键字进行升序排序,以从小到大的顺序从上到下摆放奶牛,此时的最大危险系数一定是所有摆放中最小的
证明:假设存在若
(
w
i
+
s
i
)
>
(
w
i
+
1
+
s
i
+
1
)
(w_i + s_i) > (w_{i+1} + s_{i+1})
(wi+si)>(wi+1+si+1),风险系数是所有摆放中最小的
我们可以计算交换两头奶牛前后,第i个与第i+1个位置上的危险系数
交换前:
第i个位置的危险系数:
(
w
1
+
w
2
+
.
.
.
+
w
i
−
1
−
s
i
)
(w_1+w_2+...+w_{i-1}-s_i)
(w1+w2+...+wi−1−si)
第i+1个位置的危险系数:
(
w
1
+
w
2
+
.
.
.
+
w
i
−
s
i
+
1
)
(w_1+w_2+...+w_i-s_{i+1})
(w1+w2+...+wi−si+1)
交换后:
第i个位置的危险系数:
(
w
1
+
w
2
+
.
.
.
+
w
i
−
1
−
s
i
+
1
)
(w_1+w_2+...+w_{i-1}-s_{i+1})
(w1+w2+...+wi−1−si+1)
第i+1个位置的危险系数:
(
w
1
+
w
2
+
.
.
.
+
w
i
−
1
+
w
i
+
1
−
s
i
)
(w_1+w_2+...+w_{i-1}+w_{i+1}-s_i)
(w1+w2+...+wi−1+wi+1−si)
减去这四个式子中相同项:
(
w
1
+
w
2
+
.
.
.
+
w
i
−
1
)
(w_1+w_2+...+w_{i-1})
(w1+w2+...+wi−1)
交换前:
第i个位置的危险系数:
(
−
s
i
)
(-s_i)
(−si)
第i+1个位置的危险系数:
(
w
i
−
s
i
+
1
)
(w_i-s_{i+1})
(wi−si+1)
交换后:
第i个位置的危险系数:
(
−
s
i
+
1
)
(-s_{i+1})
(−si+1)
第i+1个位置的危险系数:
(
w
i
+
1
−
s
i
)
(w_{i+1}-s_i)
(wi+1−si)
再加上:
(
s
i
+
s
i
+
1
)
(s_i+s_{i+1})
(si+si+1)
交换前:
第i个位置的危险系数:
(
s
i
+
1
)
(s_{i+1})
(si+1)
第i+1个位置的危险系数:
(
w
i
+
s
i
)
(
2
)
(w_i+s_{i})\ (2)
(wi+si) (2)
交换后:
第i个位置的危险系数:
(
s
i
)
(
3
)
(s_{i})\ (3)
(si) (3)
第i+1个位置的危险系数:
(
w
i
+
1
+
s
i
+
1
)
(w_{i+1}+s_{i+1})
(wi+1+si+1)
已知:
(
w
i
+
s
i
)
>
(
w
i
+
1
+
s
i
+
1
)
(w_i + s_i) > (w_{i+1} + s_{i+1})
(wi+si)>(wi+1+si+1),观察(2)式与(3)式,我们能得到
(
w
i
+
s
i
)
>
m
a
x
(
w
i
+
1
+
s
i
+
1
,
s
i
)
(w_i + s_i) > max(w_{i+1}+s_{i+1}, s_i)
(wi+si)>max(wi+1+si+1,si)
同时
(
w
i
+
s
i
)
>
w
i
+
1
+
s
i
+
1
>
s
i
+
1
(w_i + s_i) > w_{i+1}+s_{i+1} > s_{i+1}
(wi+si)>wi+1+si+1>si+1,所以交换前第i个位置与第i+1个位置的较大值为
(
w
i
+
s
i
)
(w_i + s_i)
(wi+si)
但是交换后第i个位置与第i+1个位置的较大值小于
(
w
i
+
s
i
)
(w_i + s_i)
(wi+si),也就是交换前第i个位置与第i+1个位置的较大值
即,交换过后危险系数变小了,与前提矛盾,所以摆放奶牛的序列中,不能存在
(
w
i
+
s
i
)
>
(
w
i
+
1
+
s
i
+
1
)
(w_i + s_i) > (w_{i+1} + s_{i+1})
(wi+si)>(wi+1+si+1),即所有奶牛的
(
w
+
s
)
(w+s)
(w+s)需要从小到大地从上往下摆放,才能得到所有摆放中最小的最大危险系数
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
struct cow
{
int s, w;
bool operator<(const cow& x)
{
return (s + w) < (x.s + x.w);
}
}cows[N];
int main()
{
int n;
scanf("%d", &n);
for (int i = 0; i < n; ++ i ) scanf("%d%d", &cows[i].w, &cows[i].s);
sort(cows, cows + n);
int res = -2e9, sum = 0;
for (int i = 0; i < n; ++ i )
{
res = max(res, sum - cows[i].s);
sum += cows[i].w;
}
printf("%d\n", res);
return 0;
}
debug:res要设置为-2e9,因为第一头牛的危险系数可能最小且为负数,这时res就要设置成一个比它还小的数