目录

题目描述

输入描述

输出描述

用例

题目解析

算法源码

---

题目描述

现有一个机器人，可放置于 M × N 的网格中任意位置，每个网格包含一个非负整数编号，当相邻网格的数字编号差值的绝对值小于等于 1 时，机器人可以在网格间移动。

问题： 求机器人可活动的最大范围对应的网格点数目。
说明：网格左上角坐标为 (0,0) ,右下角坐标为(m−1,n−1)，机器人只能在相邻网格间上下左右移动

输入描述

第 1 行输入为 M 和 N ， M 表示网格的行数 N 表示网格的列数
之后 M 行表示网格数值，每行 N 个数值（数值大小用 k 表示），
数值间用单个空格分隔，行首行尾无多余空格。
M、 N、 k 均为整数，且 1 ≤ M,N ≤ 150, 0 ≤ k ≤ 50

输出描述

输出 1 行，包含 1 个数字，表示最大活动区域的网格点数目，
行首行尾无多余空格。

用例

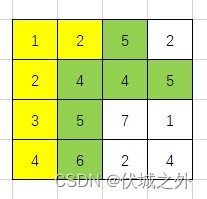
输入	4 4 1 2 5 2 2 4 4 5 3 5 7 1 4 6 2 4
输出	6
说明	图中绿色区域，相邻网格差值绝对值都小于等于 1 ，且为最大区域，对应网格点数目为 6。

题目解析

本题其实就是求最大的连通分量，相邻网格是否连通的规则如下

当相邻网格的数字编号差值的绝对值小于等于 1 时

因此，求解连通分量，我们可以使用并查集。关于并查集的知识，请看：华为机试 - 发广播_伏城之外的博客-CSDN博客_服务器广播 华为机试

算法源码

/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");

const rl = readline.createInterface({
  input: process.stdin,
  output: process.stdout,
});

const lines = [];
let m, n;
rl.on("line", (line) => {
  lines.push(line);

  if (lines.length === 1) {
    [m, n] = lines[0].split(" ").map(Number);
  }

  if (m && lines.length === m + 1) {
    lines.shift();
    const matrix = lines.map((line) => line.split(" ").map(Number));

    console.log(getResult(matrix, m, n));
    lines.length = 0;
  }
});

function getResult(matrix, m, n) {
  const ufs = new UnionFindSet(m * n);

  // 上下左右的偏移量
  const offset = [
    [-1, 0],
    [1, 0],
    [0, -1],
    [0, 1],
  ];

  for (let i = 0; i < m; i++) {
    for (let j = 0; j < n; j++) {
      // 注意下面这层for是常量级的，就四次循环，因此，这里的时间复杂度还是O(n*m)，即
      for (let k = 0; k < offset.length; k++) {
        const [offsetX, offsetY] = offset[k];
        const newI = i + offsetX;
        const newJ = j + offsetY;
        if (newI < 0 || newI >= m || newJ < 0 || newJ >= n) continue;
        if (Math.abs(matrix[i][j] - matrix[newI][newJ]) <= 1) {
          ufs.union(i * m + j, newI * m + newJ);
        }
      }
    }
  }

  let total = m * n;

  // ufs.count是连通分量的个数，如果只有一个连通分量，那么代表所有的点都可达
  if (ufs.count === 1) return total;

  // 这个for循环是有必要的，确保每个点都指向祖先
  for (let i = 0; i < total; i++) {
    ufs.find(i);
  }

  // 统计指向同一个祖先下点的个数，即每个连通分量下的点个数
  const countObj = ufs.fa.reduce((p, c) => {
    p[c] ? p[c]++ : (p[c] = 1);
    return p;
  }, {});

  // 取最大个数
  return Math.max.apply(null, Object.values(countObj));
}

class UnionFindSet {
  constructor(n) {
    this.fa = new Array(n).fill(0).map((_, i) => i);
    this.count = n;
  }

  find(x) {
    if (x !== this.fa[x]) {
      return (this.fa[x] = this.find(this.fa[x]));
    }
    return x;
  }

  union(x, y) {
    const x_fa = this.find(x);
    const y_fa = this.find(y);

    if (x_fa !== y_fa) {
      this.fa[y_fa] = x_fa;
      this.count--;
    }
  }
}