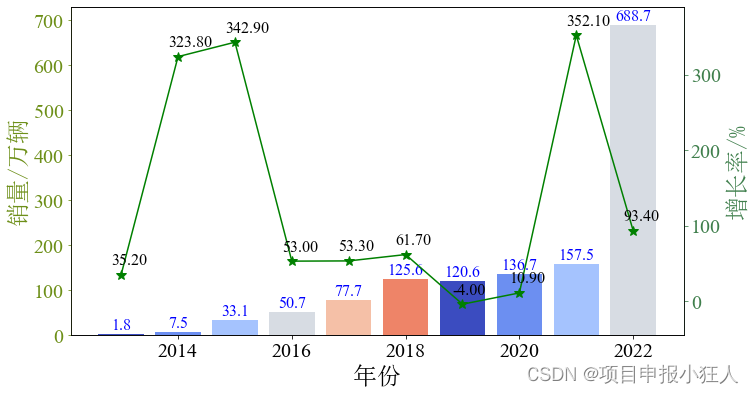
离散化方法

设f(x)是定义在[a,b]上的连续函数，当它们的表达式很复杂，甚至写不出来时，我们可以选择若干个离散点

求出f(x)在这些点处的函数值或函数值的近似值

从而得到一个如下的函数值列表：

⚠️提示：对于一个实际的控制系统来说，我们可以直接由数据采集系统获得上面的函数值列表，比如在一些离散的时刻点的温度、压力等等。 

插值方法

对于任意给出的某个函数y=f(x)的函数值列表:

 构造多项式n次多项式pn(x), 满足条件

 使用p(x)近似表示y

⚠️提示：由于pn(x)是一个多项式函数，所以求它在某一点处的函数值、在某一点处的导数值、在某个区间上的定积分所涉及的计算都是四则运算，从而我们的问题得到了解决。

逼近方法

设f(x)是满足某种特定条件的函数（比如在某个区间上连续可微、在某个区间上平方可积等），表达式比较复杂甚至写不出来，但是我们可以把它表示为一个简单函数系列{fn(x),n=1,2,…}的极限,即

  这样我们就可以根据不同的精度要求选取适当大的正数n,利用fn(x)近似替代f(x)。

⚠️提示：如果f(x)可以展为泰勒级数，那么我们可以取fn(x)为f(x)的泰勒展式前n+1项。

迭代的方法

假如我们要计算出某个实际值x*,我们可以构造一个序列{xn,n=0,1,2,…},满足条件：

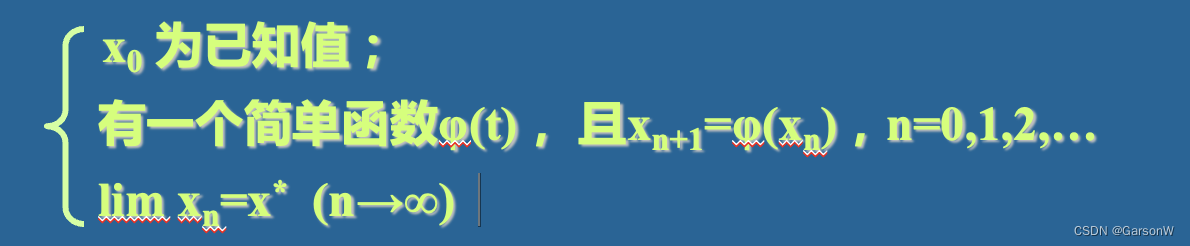
那么，我们可以反复利用xn+1=φ(xn)， 经过N 次迭代后，用xN+1 作为x* 的近似值。

⚠️提示：x0 的作用就好像是种子，迭代过程就好像农民一茬一茬地种庄稼。对于求解实际问题来说，我们还可以根据实际情况采用适当的改进措施。

迭代方法的例子：