DFS，BFS和迭代加深的联系与区别

DFS：
DFS算法是沿着搜索树的根节点，一直遍历完该搜索树之后再回溯继续搜索的一种算法。缺点是可能会出现答案在搜索树层数很浅，在靠后的子树中，但由于搜索次序需要遍历完一棵搜索树所有的节点，所以导致效率低下。

关于BFS：
BFS算法是沿着搜索树的根节点，按层遍历完该搜索树所有节点的一种算法。缺点是可能会出现答案在搜索树层数很深的地方，导致效率低下。且如果是满二叉树这样的搜索树很可能会使在BFS的过程中队列爆掉。在层数很多的时候会占用很多的空间。

关于迭代加深：
迭代加深算法其实是一种结合了DFS和BFS两种算法特点的搜索算法。我们会预设搜索的层数，然后仅在该层数以内进行DFS。这一算法很有效的避免了DFS可能会出现的效率低下的问题。
而似乎这样的算法思路和BFS相同，而且由于拓展层数的时候会重复搜索，所以反而更慢了。但其实，迭代加深有效的避免了使用大量空间的问题，相对于普通的BFS也是有优势的。

例题1. 加成序列

原题链接

普通思想：

用5距离
本题要找到
1 - 5中
满足条件的序列

那么我们指定先从1开始找
1 1得 2
1 2 _ _ _…5
1 2 3 _ _ 5
1 2 4 _ _ 5
类似于这样推

那么我们想到由于是从
1 2 延申到 第3层 有 3 和 4 两种情况

优化方法：

那么用bfs
那么有一个问题就是
bfs队列 需要存储特别多的 元素

如果用dfs呢？
首先清楚是怎么dfs的

那就是
1 2 3 _ _ 5
1 2 3 4 _ _ 5
1 2 3 5

这样就出来了

但是如果 特别大的情况

那么dfs会搜到 非常多 且没用的数据

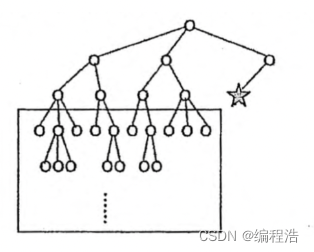
这样 我们想 能不能
dfs 层序遍历
那么也就是 叫做 dfs迭代加深算法了

也就是 按层序dfs

放到本题的思路就是

利用 规定 第一位是1
然后去dfs
参数是 当前层序，当前可遍历到的最大的层序
（这个是从代码中总结出来的，看下代码 就理解了）

具体逻辑 看看代码 就能理解

总结就是

1. 用u之前的数据 构造 第u位 的数
2. 当u==k 也就是不能再遍历了，那么判断一下u-1的数值是不是等于n 如果等于说明答案正确，如果不等于，那么继续遍历该层情况（或者是把最大遍历层数k+1继续遍历）

#include<iostream>

using namespace std;

const int N = 110;

int n;
int a[N];

bool dfs(int u,int k)
{
    if(u==k)
        return a[u-1]==n;
        
    
    for(int i = u-1; i >= 0; i--)
    {
        for(int j = i; j >= 0; j--)
        {
            int s = a[i] + a[j];
            if(s>a[u-1])
            {
                a[u] = s;
                if(dfs(u+1,k)==true)
                    return true;
            }
        }
    }
    return false;
    
}

int main()
{
    a[0] = 1;
    while(cin >> n,n)
    {
        int k = 1;
        while(dfs(1,k)==false)
        {
            k++;
        }
        for(int i = 0; i <= k-1; i++)
        {
            cout << a[i] << ' ';
        }
        cout << endl;
    }
    
    return 0;
}