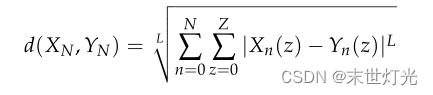本文是Quantitative Methods and Analysis: Pairs Trading此书的读书笔记。
一、APT(套利定价理论)应用于计算投资组合的风险
某个投资组合由两个股票A和B组成,它们的暴露系数向量(exposure vector)分别为和
。两个股票在投资组合中的比重为
和
。所以,投资组合的暴露系数向量为:
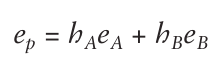
假设现在有两个因子,则暴露系数向量为:

或者表示为:
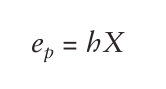
投资组合的一般因子回报的方差(common factor variance)表示为:
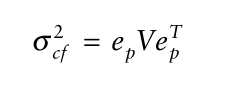
替换:

现在看看特定回报的方差(specific variance)那一部分。投资组合中两个股票的特定回报的方差是不相关的,投资组合的特定方差可以表示为组合中各个股票特定方差的加权求和:
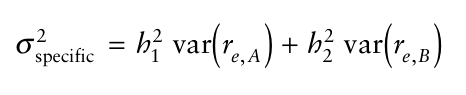
表示成矩阵的形式:

进一步简化表示:
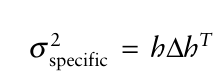
现在投资组合的风险就可以表示成如下(即投资组合回报的方差):
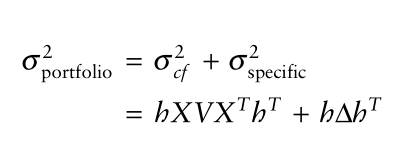
现在给出求两个投资组合Y和Z的协方差公式:
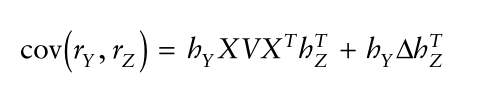
有了这些公式,我们就可以计算投资组合中的风险了。
模型也有失效的时候。注意,我们计算风险主要用到因子暴露系数以及协方差矩阵。有时候,有关于某只股票的大新闻出现,那么原来的因子暴露系数可能就不在适用了。还有就是,现实中资产回报呈现非正态的肥尾分布,而不是APT假设的正态分布。总之,就是心中有数模型会失效。
二、APT(套利定价理论)应用于计算投资组合的beta
这个beta是资产定价模型CAPM里面的beta。如果我们能够使用APT模型,为什么要计算更简单的CAPM模型的参数?这不是绕了一圈又回去了吗?是的。然而,如果我们要使用市场组合(market portfolio)对冲我们的投资组合,需要一个对冲比率(hedge ratio),而beta正是决定了这个对冲比率。所以,计算beta是有意义的。
假设一个线性组合是由两个投资组合按比率组成。这个线性组合的回报
是,其中
是投资组合的回报,
是市场的回报。使得这个线性组合的回报方差最小的
即最佳对冲比率。
下面看看,线性组合的回报方差:
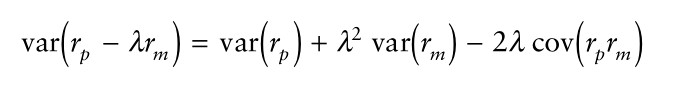
这个回报方差对求偏导数,然后令这个偏导数等于0,从而求得使得回报方差最小的
为:
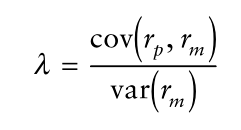
而刚好这个值就是beta值的定义(CAPM模型中beta的定义)。进一步,最佳
值得计算公式为:
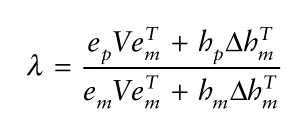
和
分别是投资组合的因子暴露系数以及市场的因子暴露系数,
和
分别是投资组合和市场的持有比重向量。我们可以使用这个方法计算最佳对冲比率。
三、APT(套利定价理论)应用于追踪蓝设计
追踪篮(a tracking basket):一篮子股票。这个篮子会追踪一个指数(index)。如果这个篮子就是指数,那么它们的价格是一样的。然而,追踪篮通常由几个股票组成,那么追踪篮的回报就不会跟指数的回报一致。这种不一致可以用追踪误差(tracking error)去描述。
追踪误差定义为追踪篮和指数之间的回报差距的标准差,而这个回报差距的均值假设为零。
考虑一个长短投资组合(long-short portfolio),其中我们好仓(long)指数,淡仓(short)追踪篮。我们期望从指数和追踪篮得到的回报是一样的。这样,我们在一头获得的收益会被另一头同样的损失中和掉。因而,期望的总回报是零。这种从零开始的变化程度可以被长短投资组合回报的标准差描述,从而形成了追踪误差的度量。
设计一个追踪蓝就包括了设计一个使得追踪误差最小的投资组合(下式是最小化追踪篮和指数之间的回报差距的方差,注意回报差距的均值/期望假设为零)。即,
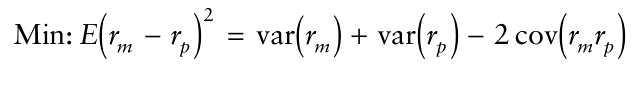
是追踪篮子的回报,
是市场的回报。使用APT,上述式子可以表达为:
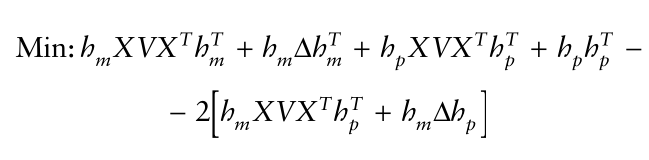
注意,市场投资组合的方差完全不受跟踪篮组成变化的影响。当我们改变跟踪篮组成时,只有两个项受到影响,那就是跟踪篮方差和协方差项。因此,最小化跟踪误差等于最小化两项之和。
跟踪误差方差(error variance)可以被视为两个分量的总和:即一般因子成分(common factor component)和特定成分(specific component)。如果我们设计一个跟踪篮子,使篮子的因子暴露系数与指数的因子暴露系数完全匹配(即使它们的组成可能不相同),那么一般因子成分将为零。我们现在只剩下方差的特定成分。特定成分对总方差的贡献要比一般因子成分的贡献小得多。此外,如果两个投资组合高度多样化,则投资组合的特定回报的期望值为零。因此,在这种情况下,跟踪误差仅仅是归因于投资组合中不同的特定回报的贡献。跟踪篮设计首先要确保因素暴露系数尽可能匹配。(最后这一段没看懂)




![[附源码]Python计算机毕业设计Django的专业技能认证系统](https://img-blog.csdnimg.cn/da7e62eeec924c1da29b56902ff61fc3.png)