😄 额,本想学学XLNet的,然后XLNet又是以transformer-XL为主要结构,然后transformer-XL做了两个改进:一个是结构上做了segment-level的循环机制,一个是在attention机制里引入了相对位置编码信息来避免不同segment的同一位置采用相同的绝对位置编码的不合理。但无奈看到相对位置编码这里我懵住了,只好乖乖追溯回去原始论文来学习学习嘿嘿🐶。
🦄 本文将以公式原理+举例的方式让你秒懂,放心食用。
🚀 RPR这论文就5页,方法部分就2页,看完结合网上理解下就ok了。
🚀 论文链接:https://arxiv.org/pdf/1803.02155.pdf
👀 三位谷歌大佬的作品:

🚀 导航
| ID | 内容 |
|---|---|
| NO.1 | 1、简单背景介绍+提出动机 |
| NO.2 | 2、何为相对位置编码 (原理+例子讲解)? |
| NO.3 | 3、RPR实现细节 |
简单背景介绍+提出动机
回顾一下RNN, LSTM类型的序列网络,对于以下输入,love 的输出是相同的。由于这类序列网络对于每个token的编码都是基于前向或后向的序列信息进行整合得到,所以并不需要显示引入位置编码信息即可学到序列的先后关系。
“I love you, do you love me?”
回顾一下原生transformer,假若我们在embedding层不加上绝对位置编码embedding,那在self-attention层会对 love 这两个位置的编码输出一样的表示,这显然是不合理的,因为他们有不同的上下文,语义肯定有所区别。
But 加上绝对位置编码就OK了吗?绝对位置编码也存在局限性:没有外推性,即如果预训练最大长度为512的话,那么最多就只能处理长度为512的句子,再长就处理不了了。当然,也可以将超过512的位置向量随机初始化,然后继续微调。
所以由于存在这个局限,相对位置编码被提出,它不存在绝对位置编码这种缺点。
何为相对位置编码 (原理+例子讲解)?
相对位置编码,顾名思义咯,一个位置相对另一个个位置的表示。它是用一组可训练的embedding向量来表示的。自己回顾下transformer的self-attention里 (如下式),在计算某个token的q与其他所有token的k进行注意力点积计算时,其时相当于以q对应的这个token为中心token,k对应的token为q的周围token。所以每个词都会有机会作为中心词计算。

self-att的输入、输出是同维度的,那么输出的每一维的计算方式如下 :

其中,注意力权重的计算方式如下,也就是将qk点积结果过softmax:

其中,点积的计算方式如下:

所以相对位置编码这时可以登场了,即中心token与周围token是有相对位置的,相对位置编码即可用来作为这种相对位置的表示。举个例子,如我们一个句子长度为4,那就一共有7个相对位置编码embedding要学习,如下:
| Index | 描述 |
|---|---|
| 0 | dist between token at position i and i-3 |
| 1 | dist between token at position i and i-2 |
| 2 | dist between token at position i and i-1 |
| 3 | dist between token at position i and i |
| 4 | dist between token at position i and i+1 |
| 5 | dist between token at position i and i+2 |
| 6 | dist between token at position i and i+3 |
如何使用RPR呢?比如以第一个love为中心token时 (记为 love_1),那很周围token做self-att时,love_1 with love_1用到的上表中的index=3对应的RPR,而I在love_1的左边第一个,所以用到的上表中的index=2对应的RPR,以此内推,即可拿到这次self-att对应的RPR的索引,用了这个索引就可以像embedding层那样,去lookup table里取对应的向量。
“I love you, do you love me?”
- ⭐提一下:【lookup table是所有单元,以token为例,就是整个词典所有token的embedding构成的矩阵。为什么叫lookup table,哪来的look up?因为实际模型运行的时候,不是把所有token变成embedding存在文件里,然后模型读取文件,而是把词变成one hot向量,one hot向量和embedding矩阵相乘得到对应词的embedding,这个过程等价于根据词在词典中的下标(one hot里1的下标)在embedding矩阵(V行E列)里查出对应行得到embedding向量,这个过程即look up。】
具体用公式表示相对位置编码的改进:
-
和原生transformer相比,就是多了红框这个东西,它是一个向量,so easy,别以为公式多我就看不懂了😄,其实就是中心token_i 和周围token_j 的相对位置编码向量 (用于计算zi 时引入)。也就是在每个v值 (输入x乘WV 得到v值) 计算出来后加上相对位置编码向量,再乘上注意力权重做聚合,得到输出向量的第 i 维的值。

-
和原生transformer相比,就是多了红框这个东西,它是一个向量,so easy,别以为公式多我就看不懂了😄,其实就是中心token_i 和周围token_j 的相对位置编码向量 (用于计算eij)。也就是在每个k值 (输入x乘WK 得到k值) 计算出来后加上相对位置编码向量,再乘上q值(输入x乘WQ 得到k值),再缩放,即得到点积缩放结果。

-
所以看完之后你肯定又会疑惑了,md,在公式 (3), (4)中 咋有两种相对位置编码即aijV 和 aijK ?是共享的还是分开的? 其实是分开的,看论文原话就知道:

-
所以 ,在self-att里的两个地方都引入了相对位置编码向量。
最大相对位置距离k的设置
论文对中心token和周围token的相对位置距离设了最大距离k来裁剪即clip,因为这样设定有个好处就是能够使模型泛化到训练时没遇到的序列长度,那确实直观理解起来就挺work。所以作者认为超出范围的位置还采用精准的位置编码大可不必。
作者在某个生成任务的数据集测试了不同k有无影响,发现 k≥2 时,性能没啥变化了,阿这。。。作者说未来需要在别的数据集进一步验证。我猜的话这个k的设定应该是个数据集的序列长度与数据类型相关。且有点类似n-gram那种味道。

clip一波后,公式表示如下:

来个例子直观理解下吧,别陷入沉思了👀:
如果中心token的索引为k,那么会有2k+1个相对位置编码向量需要学习,其中k个是其左边的,k个是其右边的,还有一个属于自己。如果长度超过2k+1,那么其右边超过k的索引全部置为k,左边超过k的索引全部置为0。下面是个长度为10的句子的例子,其中k=3,那么它到相对位置编码表中拿RPR向量的索引为:

? 你是不是又陷入沉思了?👀 解释下,token长度为10的句子,那这里每一行相当于每个token作为中心词时,token们的RPR向量的索引,有了所以就可以去RPR的lookup table取对应的RPR。如上述10x10矩阵的第一行,回到刚刚的表,因为第一个token作为中心token,即index=3,有因为ckip一波k=3,那周围token只有右边的即index=4, index=5, index=6。其他周围token超过了k=3,那就全设置为6, 6, 6。。。
| Index | 描述 |
|---|---|
| 0 | dist between token at position i and i-3 |
| 1 | dist between token at position i and i-2 |
| 2 | dist between token at position i and i-1 |
| 3 | dist between token at position i and i |
| 4 | dist between token at position i and i+1 |
| 5 | dist between token at position i and i+2 |
| 6 | dist between token at position i and i+3 |
RPR实现细节
🚀 这里说两点论文提到实现的细节
⭐ 1、因为是多头注意力,所以同一层各个注意力头共享相对位置编码embedding。
⭐ 2、并行加速细节,如何实现?
主要在于注意力计算中的缩放点积计算如何通过矩阵并行计算,在原生的transformer中,计算方式如下,dz即输出token的向量的维度:


上面只是单个中心 token_i 计算的缩放点积结果,换成矩阵并行的话,因为是批处理b,多头注意力h,所以相当于 bh 个seq_len x dz 和dz x seq_len个矩阵并行乘法。输出shape为:(b, h, seq_len, seq_len)。
而对于RPR的缩放点积表示:

这咋整?拆项得到如下表示,其实加号左边就跟原生transformer的一模一样,组织一下成矩阵,就可直接并行矩阵相乘了。右边的话因为aijK是lookup table中的一行向量,当加号左边组织成矩阵形式后 (),如果要将加号两边相加,那维度要相同才行。所以加号右边也要组织成矩阵形式。
- RPR lookup table的shape为(seq_len, seq_len, da),transpose一下维度得到 (seq_len, da, seq_len),其中RPR lookup table我们用A来表示,reshape后表示AT。
- X矩阵乘WQ 得到的矩阵shape为(b, h, seq_len, dz) , transpose一下得(seq_len, b, h, dz) ,再reshape得 (seq_len, b*h, dz);和AT 矩阵相乘得(论文里顶了da=dz): (seq_len, b*h, seq_len)。reshape一波得:(seq_len, b, h, dz)。transpose一下得(b, h, seq_len, seq_len)。
- 然后就和加号左边的维度对应上了,就可以矩阵相加了,就可以并行了!!!成功了兄弟们!!!ヾ(◍°∇°◍)ノ゙
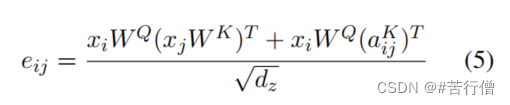
⭐看完了大家应该都懂的差不多了,如果有问题评论区留言,我有空会回复!⭐
![[附源码]计算机毕业设计JAVA小超市进销存管理系统](https://img-blog.csdnimg.cn/aa29b8e1bd3044b1ba62320d4533be9c.png)




![[MAUI] 开篇-初识MAUI](https://img-blog.csdnimg.cn/339276249a30429fa909b447ccf5e3d7.png)