0. 前言

数码相机通过将光线通过镜头投射到图像传感器上来捕捉场景产生图像。由于通过将 3D 场景投影到 2D 平面上形成图像，因此场景与其图像之间以及同一场景的不同图像之间存在重要关系。射影 (Projective geometry) 几何也称投影几何，其使用数学术语描述和表征图像形成过程。在本节中，我们将介绍多视图图像中的一些基本投影关系，并解释如何将它们用于计算机视觉应用程序。我们将学习如何通过使用投影约束使匹配更加准确，以及如何使用两视图关系拼接多个图像。

1. 相机成像原理

我们首先介绍与场景投影和图像形成相关的基本概念。自摄影开始以来，图像的生成过程从本质上来讲并没有改变。来自场景的光线被相机通过正面光圈捕捉到，然后捕获到的光线照射到位于相机背面的图像平面(或图像传感器)。此外，镜头用于汇聚来自不同场景元素的光线，该过程如下图所示：

其中，$d_o$ 是镜头到被观察物体的距离，$d_i$ 是镜头到像平面的距离，$f$ 是镜头的焦距，凸透镜成像方程 (thin lens equation) 如下：
$$\frac{1}{f}=\frac{1}{d_0}+\frac{1}{d_i}$$
在计算机视觉中，以上相机模型可以通过多种方式进行简化。首先，我们可以忽略镜头的影响，因为当相机具有无穷小光圈时其并不会改变图像外观，我们可以通过创建无限景深 (depth of field) 的图像来忽略焦距效果，在这种情况下，只需要考虑中心光线；其次，由于大部分时间 $d_o>>d_i$，我们可以假设图像平面位于焦距处；最后，我们可以从系统的几何结构中注意到平面上的图像是倒置的。我们可以通过将图像平面放置在镜头前面来获得内容相同但与水平垂直的图像，显然这在物理上是不可行的，但从数学的角度来看这两种系统是等价的。这种简化的模型通常被称为针孔相机 (pin-hole camera) 模型，其表示如下：

根据以上模型使用相似三角形定律，可以很容易地推导出将图像对象与其图像关联的基本投影方程：
$$h_i=f\frac{h_o}{d_o}$$
因此，物体(高度为 $h_o$ )的图像的大小 ($h_i$) 与其与相机的距离 ($d_o$) 成反比。这种关系描述了在给定相机几何形状的情况下，3D 场景点将被投影到图像平面的哪个位置。更具体地说，如果我们假设参考系位于焦点处，那么位于 $(X,Y,Z)$ 位置的 3D 场景点将在 $(x,y)=(f\frac{X}{Z},f\frac{Y}{Z})$ 处投影到图像平面上。其中，$Z$ 坐标对应于点的深度(或点到相机的距离，在以上等式中用 $d_o$ 表示)，这种关系可以通过引入齐次坐标将其改写成矩阵形式，其中 2D 点由三个向量表示，3D 点由四个向量表示(额外的坐标是比例因子 S，当需要从三个向量中提取二维坐标时，需要去除该比例因子 S)：
$$S\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=\left[\begin{array}{cccc}f& 0& 0& 0\\ 0& f& 0& 0\\ 0& 0& 1& 0\end{array}\right]\left[\begin{array}{c}X\\ Y\\ Z\\ 1\end{array}\right]$$
上式中的 3x4 矩阵称为投影矩阵 (projection matrix)，如果参考系未与焦点对齐，则必须引入旋转 $r$ 和平移 $t$ 矩阵，用于将投影的 3D 点表达为以相机为中心的参考系：
$$S\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=\left[\begin{array}{ccc}f& 0& 0\\ 0& f& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}{r}_1& r_2& r_3& t_1\\ r_4& r_5& r_6& t_2\\ r_7& r_8& r_9& t_3\end{array}\right]\left[\begin{array}{c}X\\ Y\\ Z\\ 1\end{array}\right]$$
以上方程的第一个矩阵包含了相机的内置参数(焦距)；第二个矩阵包含外部参数，这些参数是将相机与外部世界相关联的参数。在实际应用中，图像坐标以像素表示，而 3D 坐标以物理长度单位(例如米)表示。

2. 图像对的基本矩阵

在本节中，我们将探索显示相同场景的两个图像之间存在的投影关系。这两个图像可以通过在两个不同位置移动相机从两个视角拍摄，或使用两个相机从不同角度拍摄。从两幅或两幅以上的图像中推断出图像中每个像素点的深度信息，是立体视觉的核心研究内容。考虑使用两个摄像机观察给定的场景点，如下图所示：

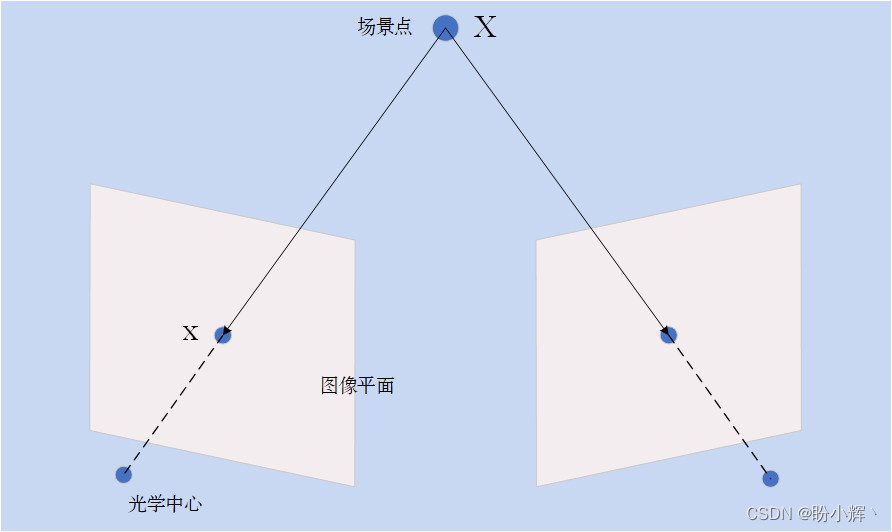
我们可以通过追踪连接此 3D 点与相机中心的线得到 3D 点 X 的图像 x。而在图像平面的位置 x 处的场景点可以位于 3D 空间中这条连线上的任何位置，这意味着如果我们想在另一幅图像中找到给定图像点的对应场景点，需要沿着中心连线在第二个图像平面上的投影进行搜索。这条假想线称为 X 点的核线 (epipolar line)，它定义了对应点必须满足的基本约束；也就是说，给定点的匹配必须在另一个视图中该点的核线上，而该核线的确切方向取决于两个相机各自的位置。事实上，核线的配置表征了双视图系统的几何形状。
可以从这个双视图系统的几何结构中得出另一结论，所有的核线都通过同一点，该点对应于一个摄像机的中心在另一台摄像机上的投影，这个特殊的点称为核 (epipole)。
在数学上，图像点与其对应的核线之间的关系可以使用 3x3 矩阵表示：
$$\left[\begin{array}{c}{l}_1^{\prime }\\ l_2^{\prime }\\ l_3^{\prime }\end{array}\right]=F\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]$$
在射影几何中，2D 线也由 3 个向量表示，它对应于满足 $l_1^{\prime }{x}^{\prime }+l_2^{\prime }{y}^{\prime }+l_3^{\prime }=0$ 方程的一组 2D 点 $(x^{\prime },y^{\prime })$ (质数上标表示这条线属于第二幅图像)。因此，基本矩阵 $F$ 可以将一个视图中的 2D 图像点映射到另一个视图中的核线。
图像对的基本矩阵可以通过求解一组方程来估计，这些方程需要两幅图像之间一定数量的已知匹配点，匹配点的最小数量为 7。

(1) 为了说明基本的矩阵估计过程，在图像对中，从 SIFT 特征的匹配结果中选择 7 个匹配，用于使用 cv::findFundamentalMat 函数计算基本矩阵。具有选定匹配项的图像对如下图所示：

(2) 如果我们将每张图像中的图像点作为 cv::keypoint 实例，首先需要将它们转换为 cv:: Point2f 以便与 cv::findFundamentalMat 一起使用：

// 关键点和描述符向量
std::vector<cv::KeyPoint> keypoints1;
std::vector<cv::KeyPoint> keypoints2;
cv::Mat descriptors1, descriptors2;

(3) selPoints1 和 selPoints2 这两个向量包含两个图像中的对应点；关键点实例用 keypoints1 和 keypoints2 表示；pointIndexes1 和 pointIndexes2 向量包含要转换的关键点的索引。cv::findFundamentalMat 函数的调用方法如下：

// 根据 7 个匹配计算 F 矩阵
cv::Mat fundamental = cv::findFundamentalMat(
            selPoints1,     // 第一张图像上的点
            selPoints2,     // 第二张图像上的点
            cv::FM_7POINT); // 7 点法

(4) 我们可以通过绘制一些选定点的核线来直观地验证基本矩阵的有效性。通过 OpenCV 函数计算出给定一组点的核线后，就可以使用 cv::line 函数绘制它们，即从左侧图像中的点计算并绘制右侧图像中的核线：

// 在右图像中绘制对应于极线的左侧图像点
std::vector<cv::Vec3f> lines1;
cv::computeCorrespondEpilines(selPoints1, 1, fund, lines1);
std::cout << "size of F matrix:" << fund.rows << "x" << fund.cols << std::endl;
// 循环所有极线
for (std::vector<cv::Vec3f>::const_iterator it=lines1.begin(); it!=lines1.end(); ++it) {
    cv::line(image2,
            cv::Point(0, -(*it)[2]/(*it)[1]),
            cv::Point(image2.cols, -((*it)[2]+(*it)[0]*image2.cols)/(*it)[1]),
            cv::Scalar(255, 255, 255));
}

绘制结果如下图所示：

核点位于核线的交点处，它是另一个相机中心的投影，该核点如上图所示。通常，核线在图像边界外相交，如果两个图像是在同一时刻拍摄的，则交点位于第一个相机可见的位置。需要注意的是，当基本矩阵仅由 7 个匹配项计算时，结果可能并不稳定，使用不同的匹配可能会得到一组差异较大的核线。
我们已经介绍了，对于一个图像中的一个点，基本矩阵给出了在另一视图中找到其对应点的直线方程。如果 $p(x,y)$ 点的对应点是 $p^{\prime }(x^{\prime },y^{\prime })$ ，且 $F$ 是两个视图之间的基本矩阵，那么由于 $p^{\prime }(x^{\prime },y^{\prime })$ 位于 $Fp$ 极线上，可以得到以下等式：
$${\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ 1\end{array}\right]}^{T}F\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=0$$
该方程表示两个对应点之间的关系，称为对极约束 (epipolar constraint)，根据此等式，可以使用已知匹配来估计矩阵项。由于 $F$ 矩阵项表示比例因子，因此只有 8 个项需要估计(第 9 个可以设置为 1)。每个匹配都可以得到一个等式，因此，使用 8 个已知匹配项，就可以通过求解所得的线性方程组来完全估计矩阵。可以通过使用 CV_FM_8POINT 标志调用 cv::findFundamentalMat 函数完成以上过程，在这种情况下，可以(并且最好)输入超过 8 个匹配项，然后求解所获得的超定线性方程组。
为了估计基本矩阵，还可以利用附加约束。数学上，$F$ 矩阵将 2D 点映射到一维线束(即在公共点相交的线)，所有这些核线都通过这个独特的点(即核点)对矩阵施加约束。此约束将估计基本矩阵所需的匹配数减少到 7 个，但在这种情况下，方程组变为非线性方程组，最多有 3 个可能的解，在这种情况下，cv::findFundamentalMat 将返回大小为 9x3 的基本矩阵，即三个 3x3 矩阵叠加。$F$ 矩阵估计的 7 匹配解可以通过使用 CV_FM_7POINT 标志调用 cv::findFundamentalMat 函数。
最后，在图像中选择合适的匹配集对于获得基本矩阵的准确估计十分重要。一般来说，匹配应该均匀的分布在整个图像上，并包括场景中不同深度的点，否则，解将变得不稳定；特别是所选场景点不应共面，因为在这种情况下基本矩阵会退化。

3. 完整代码

完整代码 estimateF.cpp 如下所示：

#include <iostream>
#include <vector>
#include <opencv2/core/core.hpp>
#include <opencv2/imgproc/imgproc.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <opencv2/features2d/features2d.hpp>
#include <opencv2/calib3d/calib3d.hpp>
#include <opencv2/objdetect/objdetect.hpp>
#include <opencv2/xfeatures2d.hpp>

int main() {
    // 读取输入图像
    cv::Mat image1= cv::imread("01.png",0);
    cv::Mat image2= cv::imread("02.png",0);
    if (!image1.data || !image2.data)
        return 0;
    cv::namedWindow("Right Image");
    cv::imshow("Right Image",image1);
    cv::namedWindow("Left Image");
    cv::imshow("Left Image",image2);
    // 关键点和描述符向量
    std::vector<cv::KeyPoint> keypoints1;
    std::vector<cv::KeyPoint> keypoints2;
    cv::Mat descriptors1, descriptors2;
    // 构建 SIFT 特征检测器
    cv::Ptr<cv::Feature2D> ptrFeature2D = cv::xfeatures2d::SIFT::create(164);
    // SURF 特征检测
    ptrFeature2D->detectAndCompute(image1, cv::noArray(), keypoints1, descriptors1);
    ptrFeature2D->detectAndCompute(image2, cv::noArray(), keypoints2, descriptors2);
    std::cout << "Number of SIFT points (1): " << keypoints1.size() << std::endl;
    std::cout << "Number of SIFT points (2): " << keypoints2.size() << std::endl;
    // 绘制关键点
    cv::Mat imageKP;
    cv::drawKeypoints(image1,keypoints1,imageKP,cv::Scalar(255,255,255),cv::DrawMatchesFlags::DRAW_RICH_KEYPOINTS);
    cv::namedWindow("Right SIFT Features");
    cv::imshow("Right SIFT Features",imageKP);
    cv::drawKeypoints(image2,keypoints2,imageKP,cv::Scalar(255,255,255),cv::DrawMatchesFlags::DRAW_RICH_KEYPOINTS);
    cv::namedWindow("Left SIFT Features");
    cv::imshow("Left SIFT Features",imageKP);
    // 构建匹配器
    cv::BFMatcher matcher(cv::NORM_L2, true);
    // 匹配两个图像的描述符
    std::vector<cv::DMatch> matches;
    matcher.match(descriptors1, descriptors2, matches);
    std::cout << "Number of matched points: " << matches.size() << std::endl;
    // 手动选择几个匹配
    std::vector<cv::DMatch> selMatches;
    // 需要确保匹配的有效性
    selMatches.push_back(matches[2]);  
    selMatches.push_back(matches[5]);
    selMatches.push_back(matches[16]);
    selMatches.push_back(matches[29]);
    selMatches.push_back(matches[14]);
    selMatches.push_back(matches[34]);
    selMatches.push_back(matches[20]);
    // 绘制所选择的匹配
    cv::Mat imageMatches;
    cv::drawMatches(image1, keypoints1,     // 第一张图像及其关键点
                image2, keypoints2,         // 第二张图像及其关键点
                selMatches,                 // 所选择的匹配
                imageMatches,               // 生成结果
                cv::Scalar(255, 255, 255),
                cv::Scalar(255, 255, 255)   /*,
                std::vector<char>(),
                2*/);
    cv::namedWindow("Matches");
    cv::imshow("Matches",imageMatches);
    // 将关键点矢量转换为 Point2f 矢量
    std::vector<int> pointIndexes1;
    std::vector<int> pointIndexes2;
    for (std::vector<cv::DMatch>::const_iterator it=selMatches.begin(); it!=selMatches.end(); ++it) {
        // 获取所选择的匹配关键点的索引
        pointIndexes1.push_back(it->queryIdx);
        pointIndexes2.push_back(it->trainIdx);
    }
    std::vector<cv::Point2f> selPoints1, selPoints2;
    cv::KeyPoint::convert(keypoints1, selPoints1, pointIndexes1);
    cv::KeyPoint::convert(keypoints2, selPoints2, pointIndexes2);
    // 绘制点
    std::vector<cv::Point2f>::const_iterator it = selPoints1.begin();
    while (it!=selPoints1.end()) {
        cv::circle(image1, *it, 3, cv::Scalar(255, 255, 255), 2);
        ++it;
    }
    it = selPoints2.begin();
    while (it!=selPoints2.end()) {
        cv::circle(image2, *it, 3, cv::Scalar(255, 255, 255), 2);
        ++it;
    }
    // 根据 7 个匹配计算 F 矩阵
    cv::Mat fundamental = cv::findFundamentalMat(
                selPoints1,     // 第一张图像上的点
                selPoints2,     // 第二张图像上的点
                cv::FM_7POINT); // 7 点法
    std::cout << "F-Matrix size= " << fundamental.rows << "," << fundamental.cols << std::endl;
    cv::Mat fund(fundamental, cv::Rect(0, 0, 3, 3));
    // 在右图像中绘制对应于极线的左侧图像点
    std::vector<cv::Vec3f> lines1;
    cv::computeCorrespondEpilines(selPoints1, 1, fund, lines1);
    std::cout << "size of F matrix:" << fund.rows << "x" << fund.cols << std::endl;
    // 循环所有极线
    for (std::vector<cv::Vec3f>::const_iterator it=lines1.begin(); it!=lines1.end(); ++it) {
        cv::line(image2,
                cv::Point(0, -(*it)[2]/(*it)[1]),
                cv::Point(image2.cols, -((*it)[2]+(*it)[0]*image2.cols)/(*it)[1]),
                cv::Scalar(255, 255, 255));
    }
    // 在左图像中绘制对应于极线的左侧图像点 
    std::vector<cv::Vec3f> lines2;
    cv::computeCorrespondEpilines(cv::Mat(selPoints2), 2, fund, lines2);
    for (std::vector<cv::Vec3f>::const_iterator it=lines2.begin(); it!=lines2.end(); ++it) {
        cv::line(image1,
                cv::Point(0, -(*it)[2]/(*it)[1]),
                cv::Point(image1.cols, -((*it)[2]+(*it)[0]*image1.cols)/(*it)[1]),
                cv::Scalar(255, 255, 255));
    }
    // 合并两张图像
    cv::Mat both(image1.rows, image1.cols+image2.cols, CV_8U);
    image1.copyTo(both.colRange(0, image1.cols));
    image2.copyTo(both.colRange(image1.cols, image1.cols+image2.cols));
    cv::namedWindow("Epilines");
    cv::imshow("Epilines", both);
    /*
    // 将关键点转换为 Point2f
    std::vector<cv::Point2f> points1, points2, newPoints1, newPoints2;
    cv::KeyPoint::convert(keypoints1, points1);
    cv::KeyPoint::convert(keypoints2, points2);
    cv::correctMatches(fund, points1, points2, newPoints1, newPoints2);
    cv::KeyPoint::convert(newPoints1, keypoints1);
    cv::KeyPoint::convert(newPoints2, keypoints2);

    cv::drawMatches(image1, keypoints1, // 第一张图像及其关键点
                image2, keypoints2,     // 第二张图像及其关键点
                matches,                // 匹配
                imageMatches,           // 结果图像
                cv::Scalar(255, 255, 255),
                cv::Scalar(255, 255, 255),
                std::vector<char>(),
                2
                ); // color of the lines
    cv::namedWindow("Corrected matches");
    cv::imshow("Corrected matches", imageMatches);
    */
   cv::waitKey();
   return 0;
}

小结

在本节中，我们介绍了多视图图像中的一些基本投影关系，并解释如何将它们用于计算机视觉应用程序，重点介绍了如何使用 cv::findFundamentalMat 函数计算基本矩阵，同时通过使用投影约束使匹配更加准确。

系列链接

OpenCV实战（1）——OpenCV与图像处理基础
OpenCV实战（2）——OpenCV核心数据结构
OpenCV实战（3）——图像感兴趣区域
OpenCV实战（4）——像素操作
OpenCV实战（5）——图像运算详解
OpenCV实战（6）——OpenCV策略设计模式
OpenCV实战（7）——OpenCV色彩空间转换
OpenCV实战（8）——直方图详解
OpenCV实战（9）——基于反向投影直方图检测图像内容
OpenCV实战（10）——积分图像详解
OpenCV实战（11）——形态学变换详解
OpenCV实战（12）——图像滤波详解
OpenCV实战（13）——高通滤波器及其应用
OpenCV实战（14）——图像线条提取
OpenCV实战（15）——轮廓检测详解
OpenCV实战（16）——角点检测详解
OpenCV实战（17）——FAST特征点检测
OpenCV实战（18）——特征匹配
OpenCV实战（19）——特征描述符