【五一创作】数据可视化之美 ( 三 ) - 动图展示 ( Python Matlab )

1 Introduction

在我们科研学习、工作生产中，将数据完美展现出来尤为重要。
数据可视化是以数据为视角，探索世界。我们真正想要的是 — 数据视觉，以数据为工具，以可视化为手段，目的是描述真实，探索世界。
数据可视化是将数据转化为易于理解和解释的图形形式的过程。它是数据分析中非常重要的一环，因为它可以帮助我们更好地理解数据、发现数据中的规律和趋势，并从中获得洞察和启示。数据可视化不仅可以帮助专业分析师更好地分析数据，还可以帮助普通用户更好地理解数据。
本博客将结合之前写过的博客系列，综合展示数据可视化之美。这次博客仅展示动图系列，所使用的工具以Python和Matlab为主。

2 案例展示

2.1 案例1 matlab实现炫酷的圣诞树

code可见往期博客：

2022年圣诞节 | matlab实现炫酷的圣诞树

当然该代码主要的部分来源这篇博客，自己仅在上面改动很少的部分：
MATLAB | 一起来绘制有雪花飘落的圣诞树叭

2.2 案例2 模型数据动态可视化

数值模型是一种数学模型，它利用计算机算法求解数学方程，将某个系统的行为进行数值化描述，从而预测系统的未来行为。数值模型广泛应用于科学、工程、金融等领域，如气象预报、流体力学、结构分析、金融风险分析等。
如果玩模型就知道，模型的输出含有大量的数据，包括时间序列上的，因此动态化的可视化模型数据就是一个很好的方式。

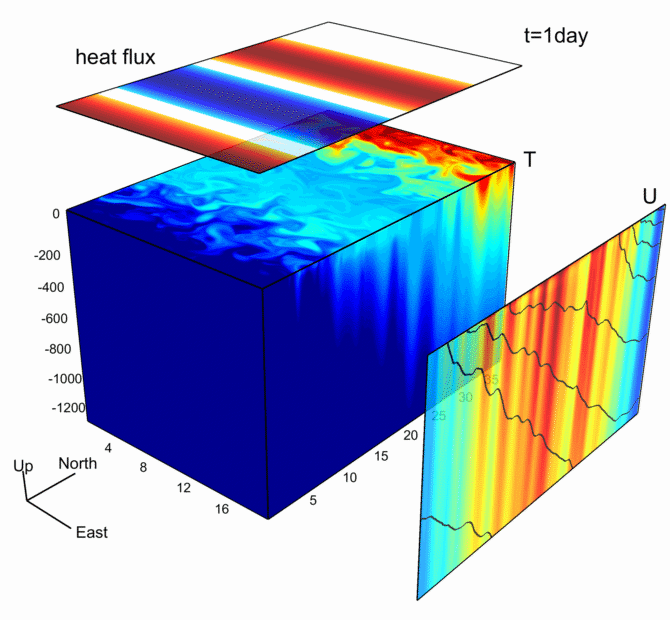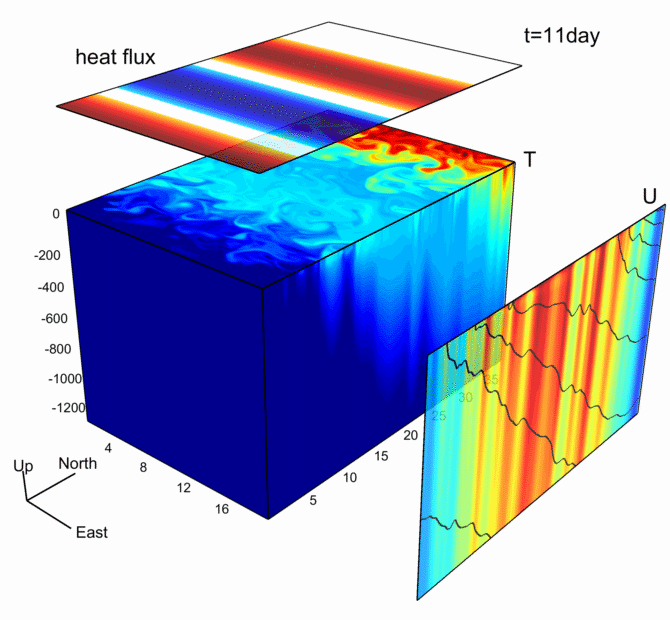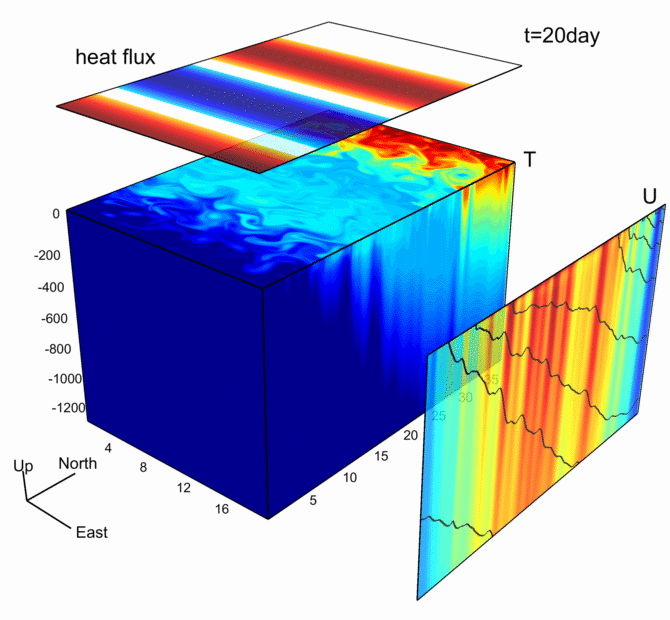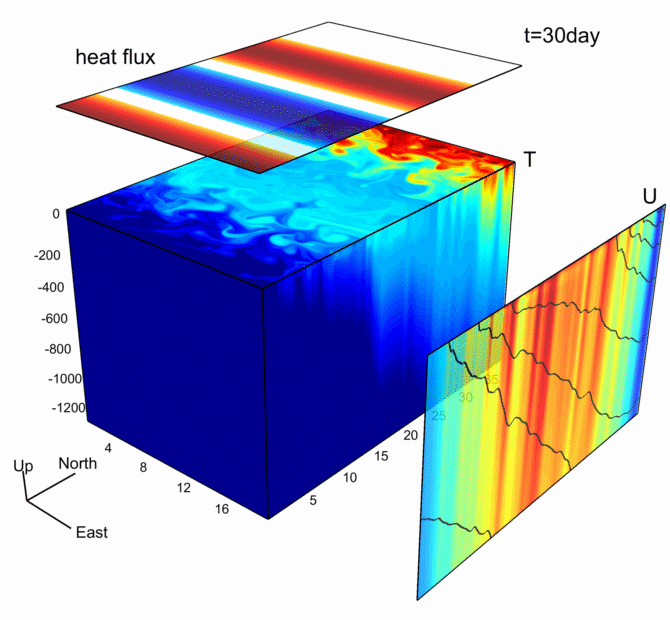
该图来源于之前的博客：
数据可视化之美-动态图绘制（以Python为工具）
最原始的图来自MITgcm，该图基于MITgcm模式输出数据绘制

2.3 案例3 SCI论文《地形对茂密森林内排放的气体在冠层内运输的影响》

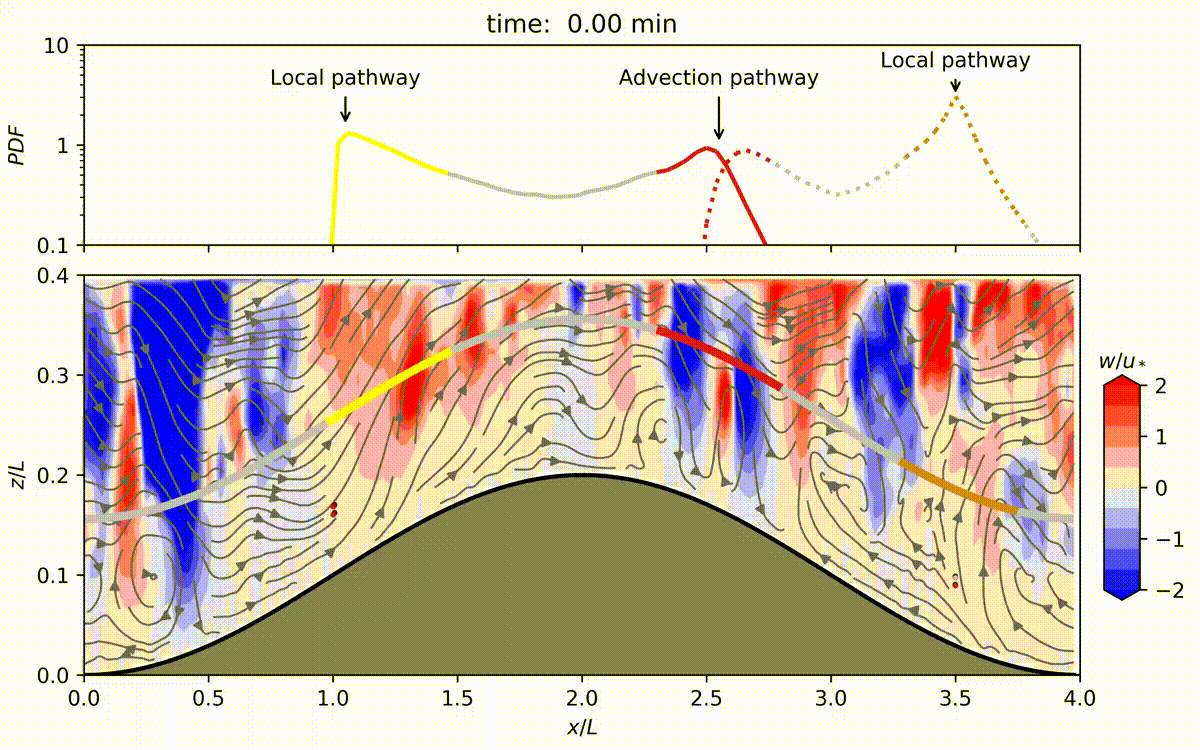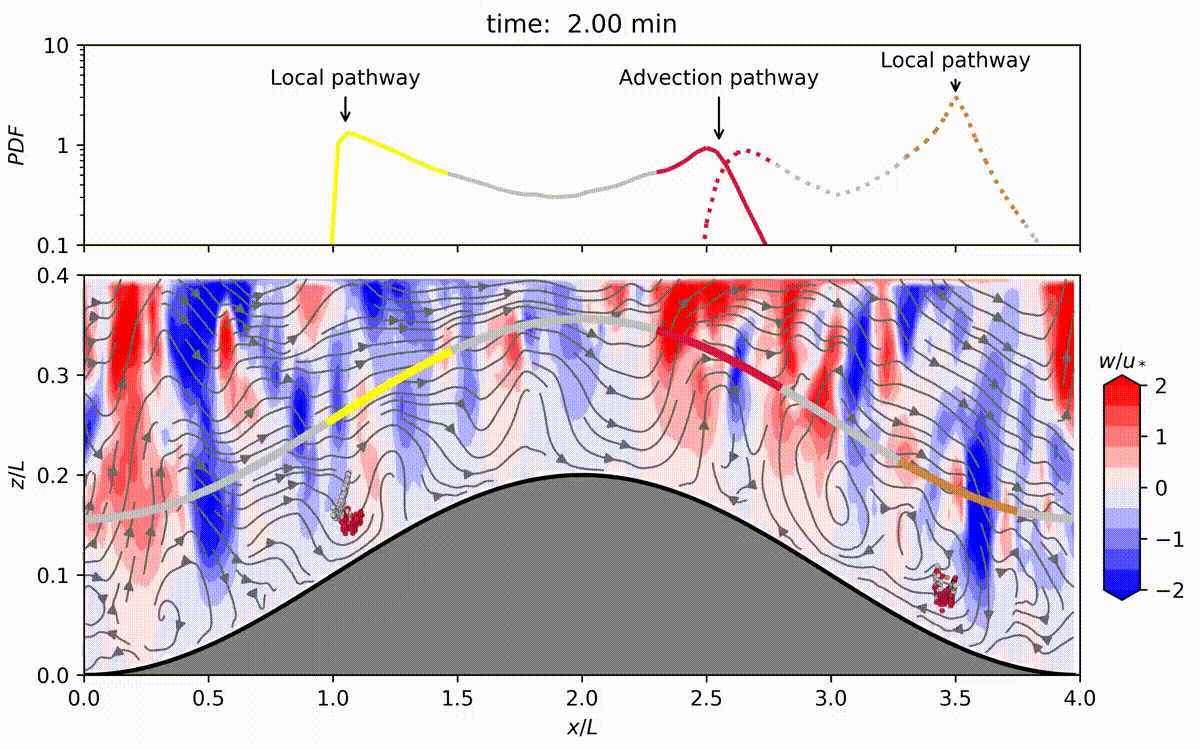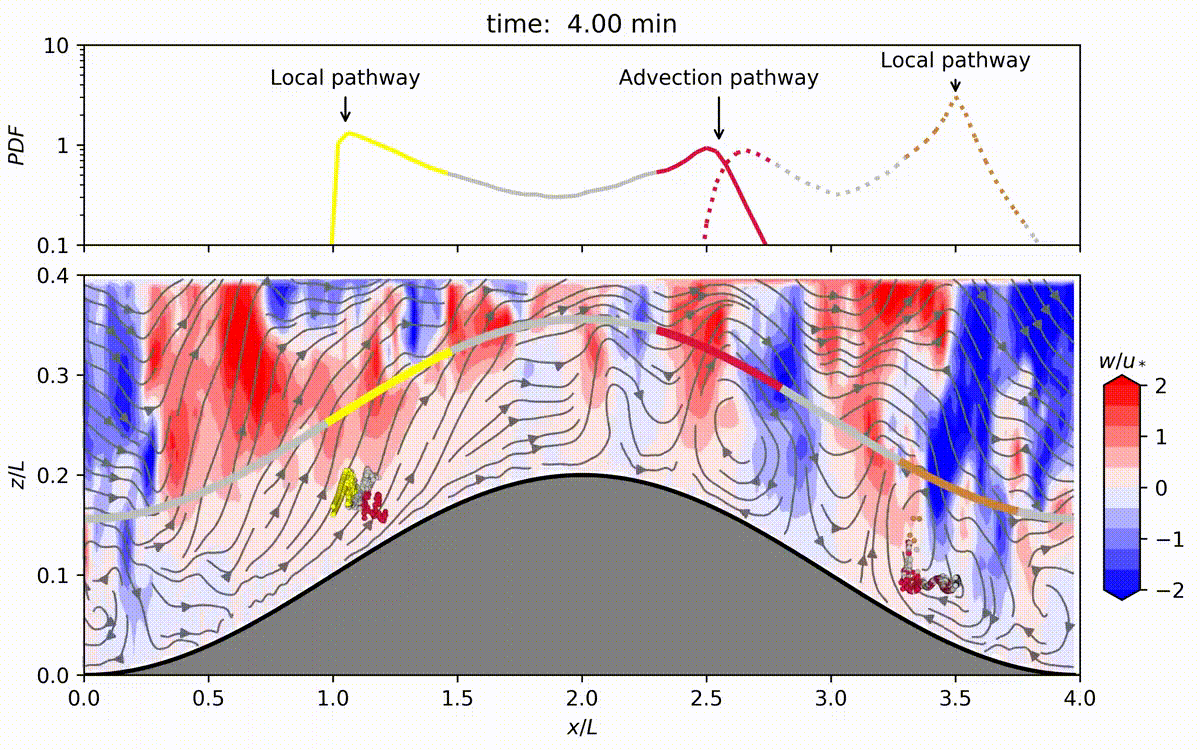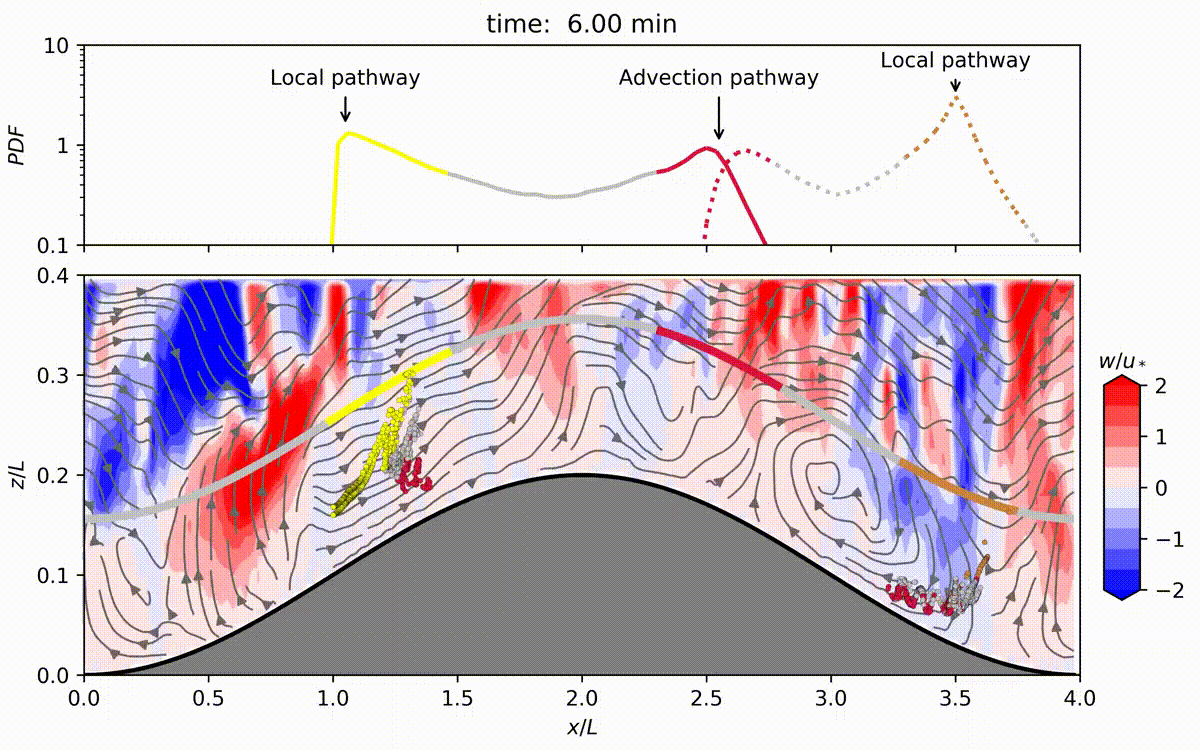
图的说明：这个动画展示了在模拟期间，连续从冠层内的四个点源不断排放的air parcels的运输情况，持续时间为2.5小时。

该动图来源于SCI论文《地形对茂密森林内排放的气体在冠层内运输的影响》 Effects of topography on in-canopy transport of gases emitted within dense forests
论文摘要：

在山地地形上的稠密林冠内部 空气流动 的意义是不容置疑的，因为它与气象学、风能、空气污染、大气化学和生态学等众多应用密切相关。虽然这种流动的数学描述很复杂，但是通过实验、数学建模以及最近的 大涡模拟（LES） 之间的相互作用，已经取得了进展。本文使用LES研究地形引起的流场变化以及这些变化如何传播到冠内的标量输运。LES运行是在一个二维正弦山脉上的高密度树林罩顶上方的中性大气边界层中进行的。叶面密度的分布使用在亚马逊雨林中收集的叶面积密度测量结果进行了指定。进行了一系列随着山峰振幅增加的LES运行，以扰动流动从其平坦地形状态中恢复。LES运行成功地再现了与先前实验室和LES研究一致的冠内区域内的回流区和山坡背风面的流动分离。模拟结果表明，释放在冠内的空气包有两个优选逃逸路径：一个类似于平坦地形中的“局部”路径和一个靠近流动分离区的“对流”路径。进一步的分析表明，优选逃脱位置在流动分离区域上导致了类似于“烟囱”的效应，对于靠近森林地面的空气包释放产生了放大作用。本文的研究表明，剪切层湍流是两个路径中的主要机制，将空气包从冠外输出。然而，与平坦地形相比，由地形引起的流动分离处的平均上升气流显著缩短了释放在较低冠层中的空气包在冠内停留的时间，从而增强了反应性气体的输出分数。

2.4 案例4 SCI 论文《时间演化的、Spatially Explicit 的北墨西哥湾缺氧区预测》

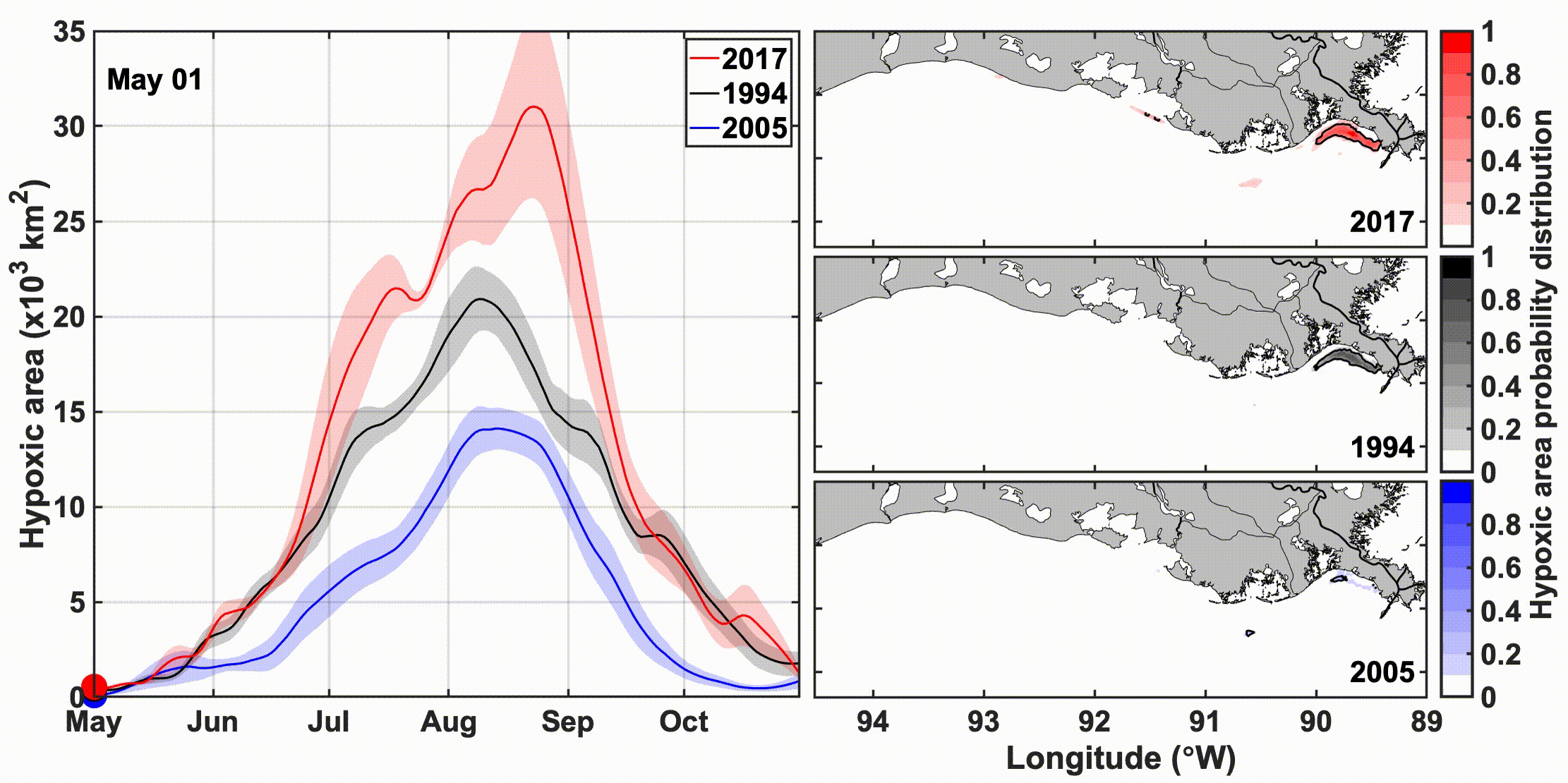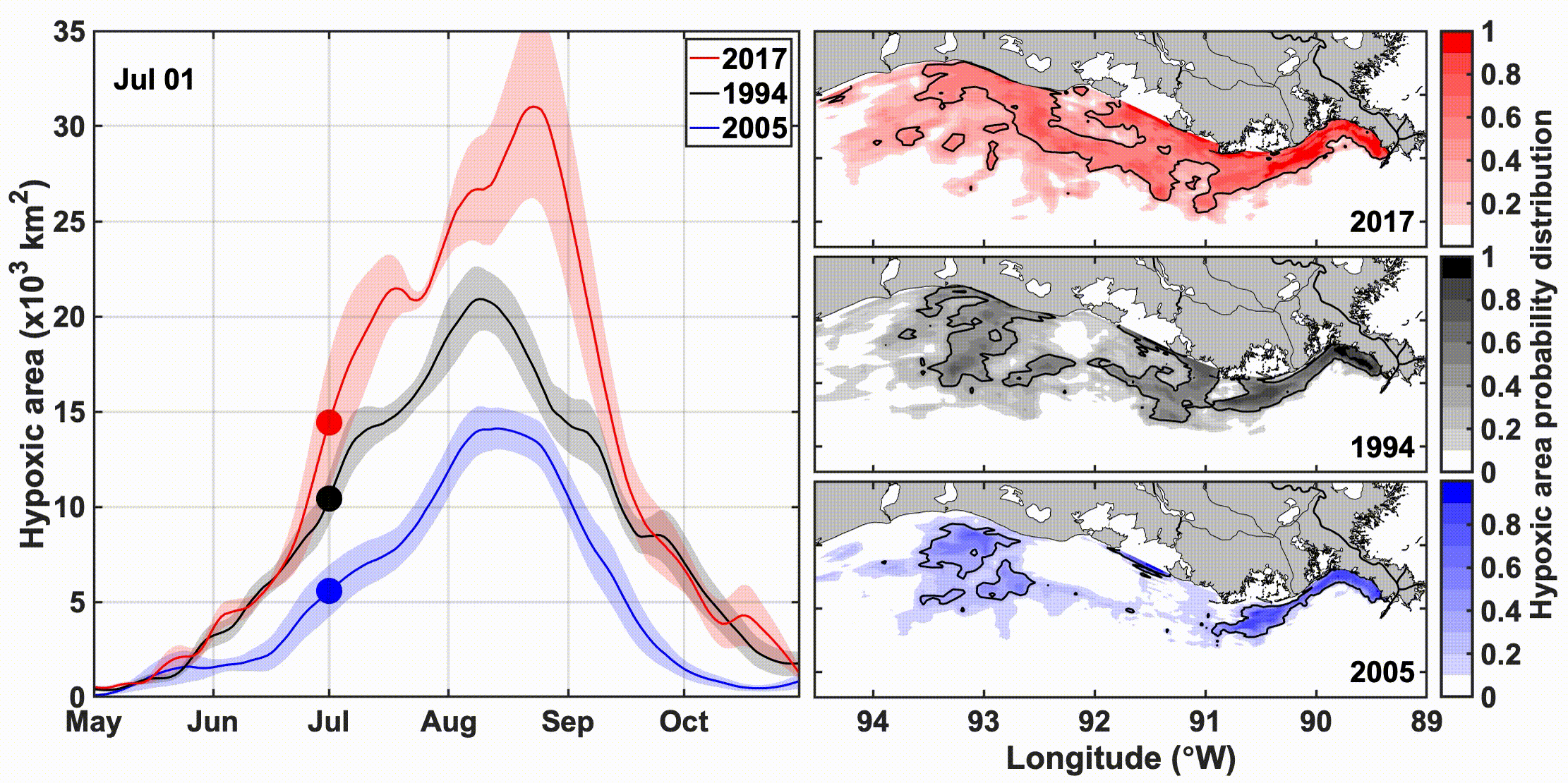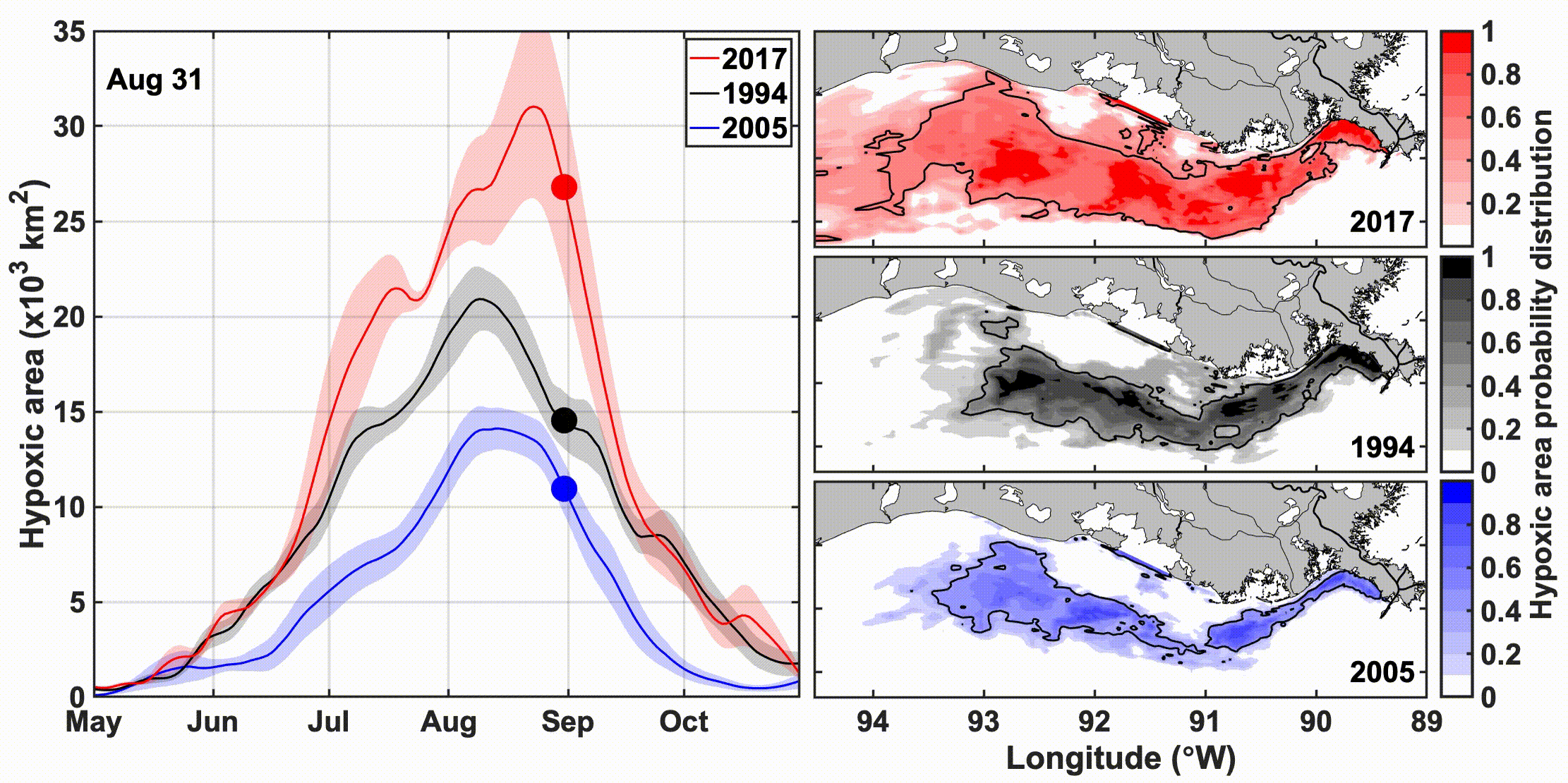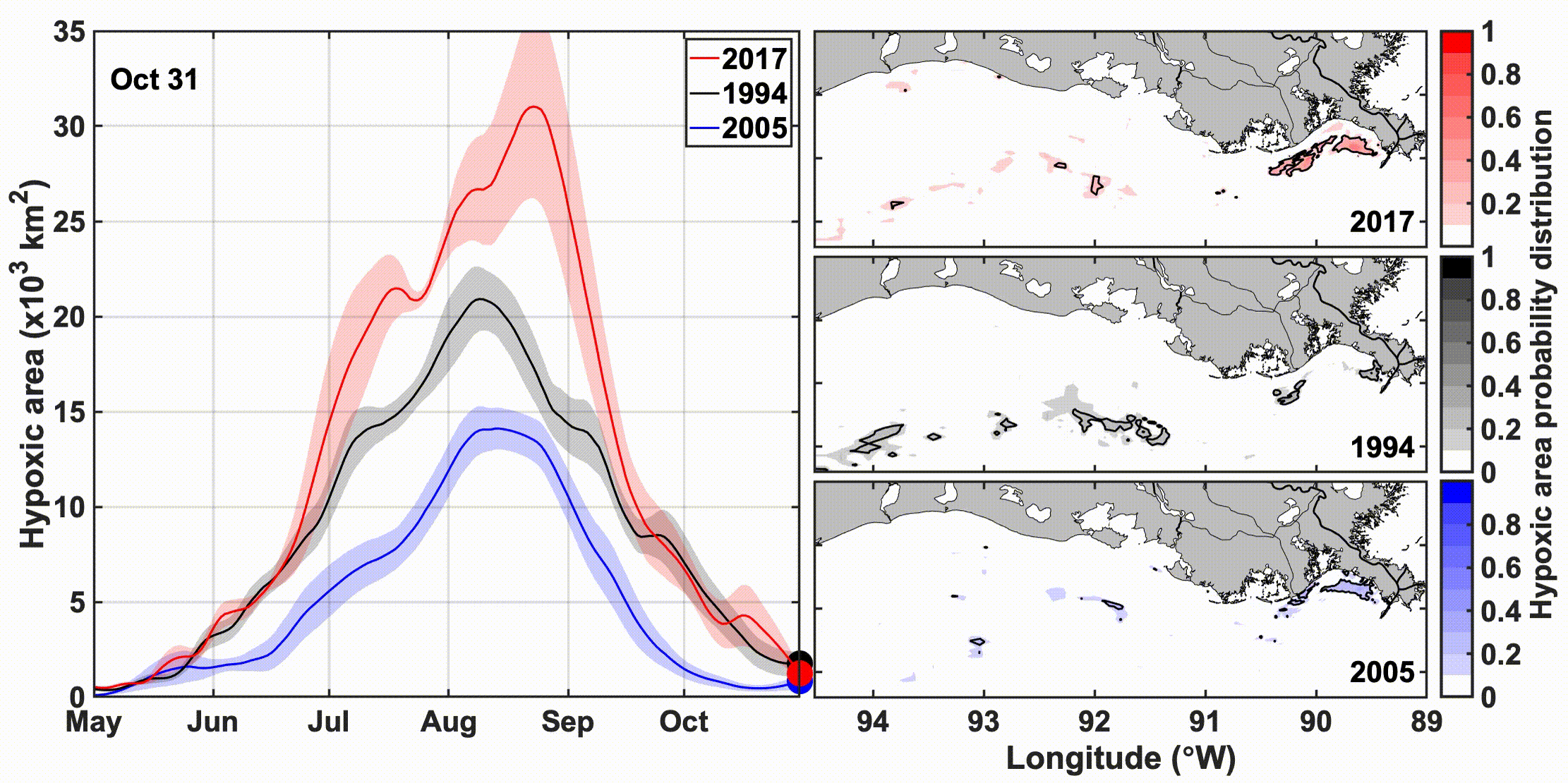
图的说明：该动图的左边反映的是缺氧区域随时间的变化，右边反映的是空间的变化

该图来自SCI论文《时间演化的、Spatially Explicit 的北墨西哥湾缺氧区预测》；该SCI论文提供了数据与源码。Time-Evolving, Spatially Explicit Forecasts of the Northern Gulf of Mexico Hypoxic Zone

下面为文章的摘要：

密西西比-阿查法莱亚河流域向北墨西哥湾输送大量淡水和营养物，促进了每年夏季大规模缺氧区的形成。长期以来，统计和半经验模型一直被用来利用春季营养负荷和中期缺氧程度的历史时间序列来提供季节性的中期缺氧程度预测。这些预测包括缺氧面积的标量估计及其不确定性，但不包括缺氧条件的空间分布或时间演化。沿海海洋的三维（3D）循环生物地球化学模型以空间显式的方式模拟缺氧的时间演化，但尚未用于季节性缺氧预测。在这里，我们提出了一种混合方法，用于季节性、空间显式、时间演化的缺氧区预测，将统计预测与3D生物地球化学模型的信息相结合。该混合方法使用春季硝酸盐负荷和多年（1985-2018年）的3D后验模拟来生成季节性预测。验证显示该方法可以解释观测到的缺氧面积年际变化高达76%。预测表明，缺氧区的最大季节性范围通常在年度巡航完成后两周的8月13日达到。由于风速和淡水排放的变化，分析了缺氧预测的月际变化，从而估计了天气相关不确定性的预测。

2.5 案例5 水下滑翔机数据可视化

Glider GIF 动图展现基于Python代码；下面为效果图
该图在博客也展示过：数据可视化之美-动态图绘制（以Python为工具）

代码开源，可见下：
这里涉及到2个数据，需要将邮件私信给作者获取。

file2read = r'otn200_sci_water_temp_live.csv'
ncfile = r'usgsCeSrtm30v1_6ebb_eec1_d277.nc'

下面是完整代码串：

from matplotlib.transforms import Bbox, TransformedBbox,  blended_transform_factory
from mpl_toolkits.axes_grid1.inset_locator import BboxPatch, BboxConnector, BboxConnectorPatch
import matplotlib.pyplot as plt
from math import radians, cos, sin, asin, sqrt
import pandas as pd
import numpy as np
import netCDF4 as nc
import imageio

file2read = r'otn200_sci_water_temp_live.csv'
ncfile = r'usgsCeSrtm30v1_6ebb_eec1_d277.nc'
data = pd.read_csv(file2read)
date = data.iloc[:, 0]
lat = data.iloc[:, 1]
lon = data.iloc[:, 2]
depth = data.iloc[:, 3]
temp = data.iloc[:, 4]
etopo2 = nc.Dataset(ncfile)
latDepth = etopo2.variables['latitude'][:]
lonDepth = etopo2.variables['longitude'][:]
topo = etopo2.variables['topo'][:]

def haversine(lon1, lat1, lon2, lat2):  # 经度1，纬度1，经度2，纬度2 （十进制度数）    
#"""    using haversin to Calculate the great circle distance between two points on the earth (specified in decimal degrees)    """ 
    lon1, lat1, lon2, lat2 = map(radians, [lon1, lat1, lon2, lat2])    
    # haversine    
    dlon = lon2 - lon1    
    dlat = lat2 - lat1    
    a = sin(dlat / 2) ** 2 + cos(lat1) * cos(lat2) * sin(dlon / 2) ** 2    
    c = 2 * asin(sqrt(a))    
    r = 6371    
    return c * r

# Compute distance along transect
dist = np.zeros((np.size(lon)))
for i in range(1, np.size(lon)):
    dist[i] = dist[i - 1] + haversine(lon[i - 1], lat[i - 1], lon[i], lat[i])

bathy = np.zeros((np.size(lon)))
for i in range(np.size(lon)):
    cost_func = np.abs(lonDepth - lon[i])
    xmin = np.where(cost_func == np.min(cost_func))[0]
    cost_func = np.abs(latDepth - lat[i])
    ymin = np.where(cost_func == np.min(cost_func))[0]
    bathy[i] = -topo[ymin, xmin]

def zoom_effect(ax1, ax2, xmin, xmax, **kwargs):

    trans1 = blended_transform_factory(ax1.transData, ax1.transAxes)
    trans2 = blended_transform_factory(ax2.transData, ax2.transAxes)
    bbox = Bbox.from_extents(xmin, 0, xmax, 1)
    mybbox1 = TransformedBbox(bbox, trans1)
    mybbox2 = TransformedBbox(bbox, trans2)
    prop_patches = kwargs.copy()
    prop_patches["ec"] = "r"
    prop_patches["alpha"] = None
    prop_patches["facecolor"] = 'none'
    prop_patches["linewidth"] = 2
    c1, c2, bbox_patch1, bbox_patch2, p = \
        connect_bbox(mybbox1, mybbox2,
                     loc1a=3, loc2a=2, loc1b=4, loc2b=1,
                     prop_lines=kwargs, prop_patches=prop_patches)
    ax1.add_patch(bbox_patch1)
    ax2.add_patch(bbox_patch2)
    ax2.add_patch(c1)
    ax2.add_patch(c2)
    ax2.add_patch(p)
    return c1, c2, bbox_patch1, bbox_patch2, p

def connect_bbox(bbox1, bbox2,
                 loc1a, loc2a, loc1b, loc2b,
                 prop_lines, prop_patches=None):
    # Fuctions for zoom effect ****************************************************
    if prop_patches is None:
        prop_patches = prop_lines.copy()
        prop_patches["alpha"] = prop_patches.get("alpha", 1) * 0.2
    c1 = BboxConnector(bbox1, bbox2, loc1=loc1a, loc2=loc2a, **prop_lines)
    c1.set_clip_on(False)
    c2 = BboxConnector(bbox1, bbox2, loc1=loc1b, loc2=loc2b, **prop_lines)
    c2.set_clip_on(False)
    bbox_patch1 = BboxPatch(bbox1, **prop_patches)
    bbox_patch2 = BboxPatch(bbox2, **prop_patches)
    p = BboxConnectorPatch(bbox1, bbox2,
                           # loc1a=3, loc2a=2, loc1b=4, loc2b=1,
                           loc1a=loc1a, loc2a=loc2a, loc1b=loc1b, loc2b=loc2b,
                           **prop_patches)
    p.set_clip_on(False)
    return c1, c2, bbox_patch1, bbox_patch2, p

# Make plots
nframes = 20
overlap = 0.95
window = np.floor(max(dist) - min(dist)) / (nframes - (nframes * overlap) + overlap)
xmin = 0
xmax = xmin + window
cmp = plt.cm.get_cmap('jet', 16)
fig1 = plt.figure()
for i in range(0, nframes):
    ax1 = plt.subplot(211)
    plt.fill_between(dist, bathy, 1000, color='k')
    plt.scatter(dist, np.asarray(depth), s=15, c=temp,
                cmap = cmp, marker='o', edgecolor='none')
    plt.ylim((-0.5, max(depth) + 5))
    ax1.set_ylim(ax1.get_ylim()[::-1])
    cbar = plt.colorbar(orientation='vertical', extend='both')
    cbar.ax.set_ylabel('Temperature ($^\circ$C)')
    plt.title('OTN Glider transect')
    plt.ylabel('Depth (m)')
    ax1.set_xlim(min(dist), max(dist))
    
    ax2 = plt.subplot(212)
    plt.fill_between(dist, bathy, 1000, color='k')
    plt.scatter(dist, depth, s=15, c=temp,
                cmap= cmp, marker='o', edgecolor='none')
    plt.ylim((-0.5, max(depth) + 5))
    ax2.set_ylim(ax2.get_ylim()[::-1])
    plt.ylabel('Depth (m)')
    plt.xlabel('Distance along transect (km)')
    ax2.set_xlim(xmin, xmax)
    zoom_effect(ax1, ax2, xmin, xmax)

    file2write = './fig/glider_' + '%02d'%i + '.png'
    plt.savefig(file2write, bbox_inches='tight')
    plt.close()
    xmin = xmax - np.floor(window * overlap)
    xmax = xmin + window

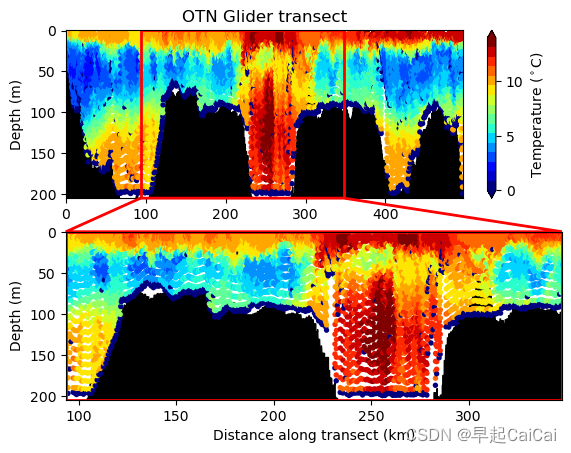
单独一个snapshot是酱纸的，见下图：
将多个snapshot合成mp4就是个完整的动图啦

3 Summary

本博客展示了五个数据可视化的案例，涵盖了不同领域和不同工具的应用。数据可视化是将数据转化为易于理解和解释的图形形式的过程，能够帮助我们更好地理解数据、发现数据中的规律和趋势，并从中获得洞察和启示。在科研学习和工作生产中，数据可视化尤为重要，能够为我们探索世界提供非常有力的工具和手段。本博客所展示的动图系列，使用了Python和Matlab等工具，通过动态可视化数据，将数据转化为视觉图像，让数据更加生动、直观、易于理解。

4 Reference

[1] 2022年圣诞节 | matlab实现炫酷的圣诞树
[2] MATLAB | 一起来绘制有雪花飘落的圣诞树叭
[3] 数据可视化之美-动态图绘制（以Python为工具）
[4] MITgcm模型官网
[5] SCI论文: Effects of topography on in-canopy transport of gases emitted within dense forests
[6] SCI论文: Time-Evolving, Spatially Explicit Forecasts of the Northern Gulf of Mexico Hypoxic Zone
[7] 数据可视化之美-动态图绘制（以Python为工具）