前言

2018年我写过一篇博客，叫：《一文读懂目标检测：R-CNN、Fast R-CNN、Faster R-CNN、YOLO、SSD》，该文相当于梳理了2019年之前CV领域的典型视觉模型，比如

2014 R-CNN
2015 Fast R-CNN、Faster R-CNN
2016 YOLO、SSD
2017 Mask R-CNN、YOLOv2
2018 YOLOv3

随着2019 CenterNet的发布，特别是2020发布的DETR(End-to-End Object Detection with Transformers)之后，自此CV迎来了生成式下的多模态时代

2020年
5月 DETR
6月 DDPM(即众人口中常说的扩散模型diffusion model)
10月 DDIM、Vision Transformer
2021年
1月 CLIP、DALL·E
3月 Swin Transformer
11月 MAE、Swin Transformer V2
2022年
1月 BLIP
4月 DALL·E 2
8月 Stable Diffusion、BEiT-3、Midjourney V3
2023年
1月 BLIP2
3月 Visual ChatGPT、GPT-4、Midjourney V5
4月 SAM(Segment Anything Model)

但看这些模型接二连三的横空出世，都不用说最后爆火的GPT4，便可知不少CV同学被卷的不行

说到GPT4，便不得不提ChatGPT，实在是太火了，改变了很多行业，使得国内外绝大部分公司的产品、服务都值得用LLM全部升级一遍(比如微软的365 Copilot、阿里所有产品、金山WPS等等)

而GPT4相比GPT3.5或GPT3最本质的改进就是增加了多模态的能力，使得ChatGPT很快就能支持图片的输入形式，从而达到图生文和文生图的效果，而AI绘画随着去年stable diffusion和Midjourney的推出，使得文生图火爆异常，各种游戏的角色设计、网上店铺的商品/页面设计都用上了AI绘画这样的工具，更有不少朋友利用AI绘画取得了不少的创收，省时省力还能赚钱，真香

但面对这么香的技术，其背后的一系列原理到底是什么呢，本文特从头开始，不只是简单的讲一下扩散模型的原理，而是在反复研读相关论文之后，准备把20年起相关的CV多模态模型全部梳理一遍，从VE、VAE、到ViT/Swin transformer、CLIP/BLIP，再到stable diffusion、GPT4，尽可能写透彻每一个模型的原理，就当2020年之后的CV视觉发展史了

过程中会尽可能写透彻每一个模型的原理，举个最简单的例子，网上介绍VAE的文章都太数学化(更怕那种表面正确其实关键的公式是错的误导人)，如果更边推导边分析背后的理论意义(怎么来的出发点是什么为什么要这么做这么做的意义是什么)，则会更好理解，这就跟变介绍原理边coding实现会更好理解、理解更深一个道理

第一部分编码器VE与变分自编码器VAE

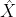1.1 AE：编码器(数据 $X$ 压缩为低维表示 $z$ )-解码器(低维表示恢复为原始数据 $\hat{X}$ )架构

自编码器(Autoencoder，简称AE)是一种无监督学习的神经网络，用于学习输入数据的压缩表示。具体而言，可以将其分为两个部分：编码器和解码器

编码器：编码器是一个神经网络，负责将输入数据 $X$ （如图像、文本等）压缩为一个低维表示 $z$ ，且表示为 $z = g(X)$
解码器：解码器是另一个神经网络，负责将编码器生成的低维表示恢复为原始数据 $\hat{X}$ ，且表示为 $\hat{X} = f(z)$

从而最终完成这么一个过程： $X \rightarrow z \rightarrow \hat{X}$ ，而其训练目标即是最小化输入数据 $X$ 与解码器重建数据 $\hat{X}$ 之间的差异，所以自编码器常用的一个损失函数为 $l = || X - \hat{X} || ^2$

这个自编码的意义在于

模型训练结束后，我们就可以认为编码 $z$ 囊括了输入数据 $X$ 的大部分信息，也因此我们可以直接利用 $z$ 表达原始数据，从而达到数据降维的目的
解码器只需要输入某些低维向量 $z$ ，就能够输出高维的图片数据 $\hat{X}$ ，那我们能否把解码器模型直接当做生成模型，在低维空间中随机生成某些向量 $z$ ，再喂给解码器 $f(z)$ 来生成图片呢？

对于第二点，理论上可以这么做，但绝大多数随机生成的 $z,f(z)$ 只会生成一些没有意义的噪声，之所以如此，原因在于没有显性的对 $z$ 的分布 $p(z)$ 进行建模，我们并不知道哪些 $z$ 能够生成有用的图片。而且我们用来训练 $f(z)$ 的数据是有限的， $f$ 可能只会对极有限的 $z$ 有响应。而整个低维空间又是一个比较大的空间，如果只在这个空间上随机采样的话，我们自然不能指望总能恰好采样到能够生成有用的图片的 $z$

有问题自然便得探索对应的解决方案，而VAE(自变分编码器，Variational Autoencoders)则是在AE的基础上，显性的对 $z$ 的分布 $p(z)$ 进行建模(比如符合某种常见的概率分布)，使得自编码器成为一个合格的生成模型

1.2 Variational AutoEncoder (VAE)

1.2.1 VAE：标数据的分布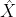 $\hat{X}$ 和目标分布 $X$ 尽量接近

VAE和GAN一样，都是从隐变量 $Z$ 生成目标数据，具体而言，先用某种分布随机生成一组隐变量 $Z = \left \{ Z_1,Z_2,\cdots ,Z_k \right \}$ (假设隐变量服从正态分布)，然后这个 $Z$ 隐变量经过一个生成器生成一组数据 $\hat{X} = \left \{ \hat{X_1},\hat{X_2},\cdots ,\hat{X_k} \right \}$ ，具体如下图所示(本1.2节的部分图来自苏建林)：

而VAE和GAN都希望这组生成数据的分布 $\hat{X}$ 和目标分布 $X$ 尽量接近，看似美好，但有两个问题

一方面，“尽量接近”并没有一个确定的关于 $\hat{X}$ 和 $X$ 的相似度的评判标准，比如KL散度便不行，原因在于KL散度是针对两个已知的概率分布求相似度的，而 $\hat{X}$ 和 $X$ 的概率分布目前都是未知(只有采样数据没有分布表达式)
二方面，经过采样出来的每一个 $Z_k$ ，不一定对应着每一个原来的 $X_k$ ，故最后没法直接最小化 $D^2(X_k,\hat{X_k})$

实际是怎么做的呢，事实上，与自动编码器由编码器与解码器两部分构成相似，VAE利用两个神经网络建立两个概率密度分布模型：

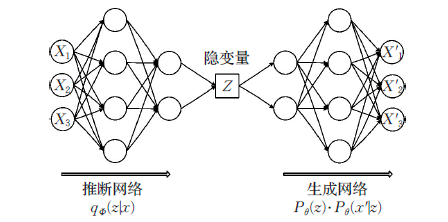
一个用于原始输入数据 $X=\{X_1,...,X_k\}$ 的变分推断，生成隐变量 $Z$ 的变分概率分布 $p(Z|X_k)$ ，称为推断网络
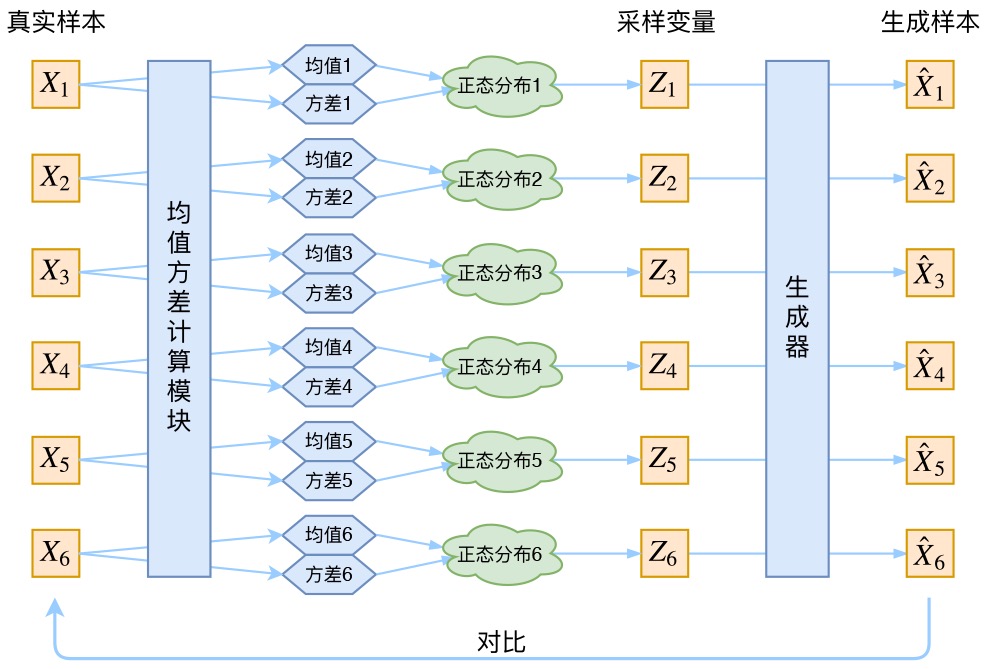
而VAE的核心就是，我们不仅假设 $p(Z)$ 是正态分布，而且假设每个 $p(Z|X_k)$ 也是正态分布。什么意思呢？即针对每个采样点 $X_k$ 获得一个专属于它和 $Z$ 的一个正态分布 $p(Z|X_k)$
换言之，有 $k$ 个 $X$ sample，就有 $k$ 个正态分布 $p(Z|X_k)$ ，毕竟没有任何两个采样点是完全一致的，而后面要训练一个生成器 $\hat{X_k}=f(Z)$ ，希望能够把从分布 $p(Z|X_k)$ 采样出来的一个 $Z_k$ 还原为 $X_k$ ，而如果从 $p(Z)$ 中采样一个 $Z_k$ ，没法知道这个 $Z_k$ 对应于真实的 $X_k$ 呢？现在 $p(Z|X_k)$ 专属于 $X_k$ ，我们有理由说从这个分布采样出来的 $Z_k$ 可以还原到对应的 $X_k$ 中去
而如何确定这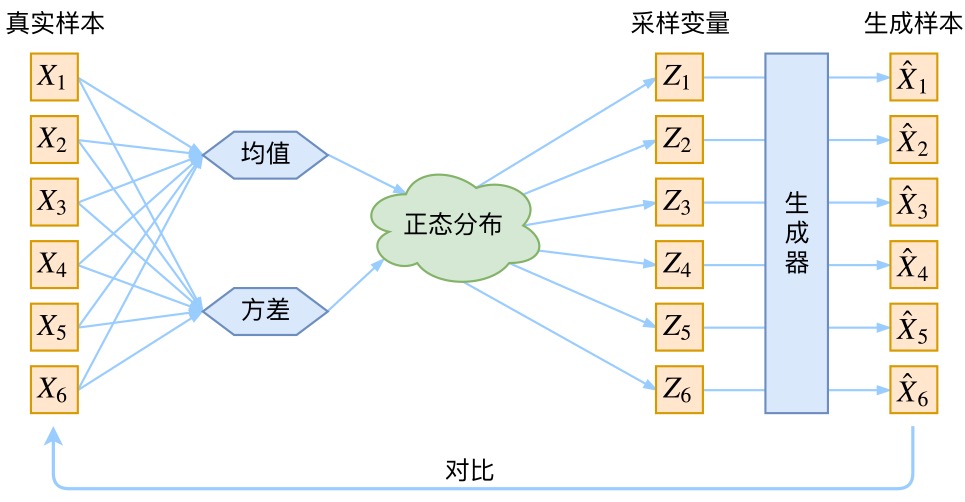 $k$ 个正态分布呢，众所周知，确定一个正太分布只需确定其均值 $u$ 和方差 $\sigma ^2$ 即可，故可通过已知的 $X_k$ 和假设的 $Z$ 去确定均值和方差
具体可以构建两个神经网络 $\mu _k = f_1(X_k)$ ， $log \sigma _{k}^{2} = f_2(X_k)$ 去计算。值得一提的是，选择拟合 $log \sigma _{k}^{2}$ 而不是直接拟合 $\sigma _{k}^{2}$ ，是因为 $\sigma _{k}^{2}$ 总是非负的，需要加激活函数处理，而拟合 $log \sigma _{k}^{2}$ 不需要加激活函数，因为它可正可负
另一个根据生成的隐变量 $Z$ 的变分概率分布 $p(Z)$ ，还原生成原始数据的近似概率分布 $p(\hat{X}|Z)$ ，称为生成网络
因为已经学到了这 $k$ 个正态分布，那可以直接从专属分布 $p(Z|X_k)$ 中采样一个 $Z_k$ 出来，然后经过一个生成器得到 $\hat{X_k} = f(Z_k)$ ，那接下来只需要最小化方差 $D^2(X_k,\hat{X_k})$ 就行

仔细理解的时候有没有发现一个问题？为什么在文章最开头，我们强调了没法直接比较 $X$ 与 $\hat{X}$ 的分布，而在这里，我们认为可以直接比较这俩？注意，这里的 $Z_k$ 是专属于或针对于 $X_k$ 的隐变量，那么和 $\hat{X_k}$ 本身就有对应关系，因此右边的蓝色方框内的“生成器”，是一一对应的生成。

另外，大家可以看到，均值和方差的计算本质上都是encoder。也就是说，VAE其实利用了两个encoder去分别学习均值和方差

1.2.2 VAE的Variational到底是个啥

这里还有一个非常重要的问题：由于我们通过最小化 $D^2(X_k,\hat{X_k})$ 来训练右边的生成器，最终模型会逐渐使得 $X_k$ 和 $\hat{X_k}$ 趋于一致。但是注意，因为 $Z_k$ 是重新随机采样过的，而不是直接通过均值和方差encoder学出来的，这个生成器的输入 $Z$ 是有噪声的

仔细思考一下，这个噪声的大小其实就用方差来度量。为了使得分布的学习尽量接近，我们希望噪声越小越好，所以我们会尽量使得方差趋于 0
但是方差不能为 0，因为我们还想要给模型一些训练难度。如果方差为 0，模型永远只需要学习高斯分布的均值，这样就丢失了随机性，VAE就变成AE了……这就是为什么VAE要在AE前面加一个Variational：我们希望方差能够持续存在，从而带来噪声！
那如何解决这个问题呢？其实保证有方差就行，但是VAE给出了一个优雅的答案：不仅需要保证有方差，还要让所有 $p(Z|X)$ 趋于标准正态分布 $N(0,1)$ ，根据定义可知
$P(Z) = \sum_{X}^{} p(Z|X)p(X) = \sum_{X}^{} N(0,1)p(X) = N(0,1)\sum_{X}p(X) = N(0,1)$
这个式子的关键意义在于告诉我吗：如果所有 $p(Z|X)$ 都趋于 $N(0,1)$ ，那么我们可以保证 $p(Z)$ 也趋于 $N(0,1)$ ，从而实现先验的假设，这样就形成了一个闭环！那怎么让所有 $p(Z|X)$ 趋于 $N(0,1)$ 呢？还是老套路：加loss
到此为止，我们可以把VAE进一步画成：

现在我们来回顾一下VAE到底做了啥。VAE在AE的基础上

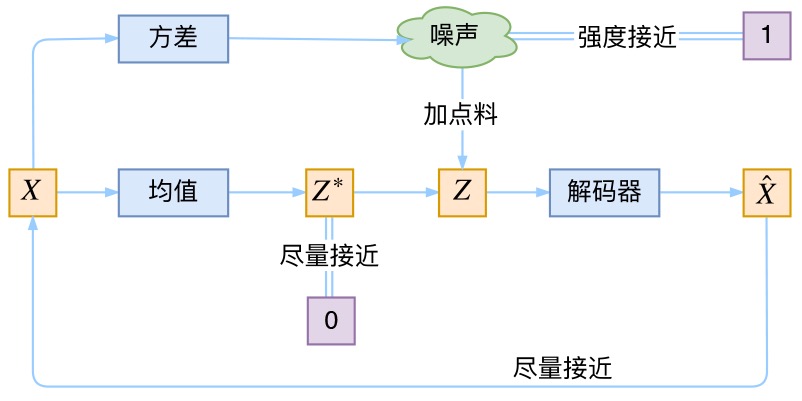
一方面，对均值的encoder添加高斯噪声(正态分布的随机采样)，使得decoder(即生成器)有噪声鲁棒性
二方面，为了防止噪声消失，将所有 $p(Z|X)$ 趋近于标准正态分布，将encoder的均值尽量降为 0，而将方差尽量保持住

这样一来，当decoder训练的不好的时候，整个体系就可以降低噪声；当decoder逐渐拟合的时候，就会增加噪声

第二部分扩散模型DDPM：Denoising Diffusion Probabilistic Models

2020年，UC Berkeley等人的Jonathan Ho等人通过论文《Denoising Diffusion Probabilistic Models》正式提出DDPM

在写本文之前，我反复看了网上很多阐述DDPM的文章，实话说，一开始看到那种一上来就一堆公式的，起初确实看不下去，虽然后来慢慢的都看得下去了，但如果对于一个初次接触DDPM的初学者来说，一上来一堆公式确实容易把人绕晕，但如果没有公式，则又没法透彻理解背后的算法步骤，两相权衡，本文将侧重算法每一步的剖析，而公式更多为解释算法原理而服务，说白了，侧重原理其次公式，毕竟原理透彻了，公式也就自然而然的能写出来了

首先，明确DDPM的目标：作为一个生成式模型，其目标是从随机噪声直接生成图片,换言之，首先训练一个噪声估计模型，然后将输入随机噪声还原成图片)，相当于就两个关键，一个是训练过程，一个是推理过程

训练过程：随机生成噪声 $\epsilon$ ，经过 $T$ 步将噪声扩散到输入原始图片 $x_0$ 中，破坏后的图片 $x_t$ ，学习破坏图片的预估噪声 $\epsilon _\theta (x_t,t)$ ，用L2 loss约束与 $\epsilon$ 原始输入噪声的距离
推理过程就输入噪声，经过预估噪声模型还原成图片

2.1 前向过程：通过高斯噪音随机加噪，相当于给图片打马赛克

前向过程（forward process）又称为扩散过程（diffusion process），简单理解就是对原始图片�0 通过逐步加高斯噪声变成 �� ，从而达到破坏图片的目的，如下图

DDPM的前向过程

用公式表示就是

(1)��=��−1+1−��−1

其中 {��}�=1� 是预先设定好的超参数，被称为Noise schedule，通常是一些列很小的值。 ��−1∼�(0,1) 是高斯噪声。由公式（1）迭代推导，可以直接得出 �0 到 �� 的公式（详细过程可见[2]），如下，

(2)��=��¯�0+1−��¯�

其中 ��¯=∏�� ，这是随Noise schedule设定好的超参数， �∼�(0,1) 也是一个高斯噪声。公式（1）或（2）就可以用来描述前向过程了，（1）用于将一张图片逐步破坏，（2）用于一步到位破坏。

2.2 反向过程（去噪）

反向过程就是通过估测噪声，多次迭代逐渐将被破坏的 �� 恢复成 �0 ，如下图

DDPM的反向过程

用公式表示就是

由于公式（2）中的真实噪声 � 在复原过程中不允许使用，因此DDPM的关键就是训练一个由 �� 和 � 估测噪声的模型 ��(��,�) ，其中 � 就是模型的训练参数， �� 也是一个高斯噪声 ��∼�(0,1) ，用于表示估测与实际的差距。在DDPM中，使用U-Net作为估测噪声的模型。