目录

题目描述

输入描述

输出描述

用例

题目解析

算法源码

---

题目描述

假设知道某段连续时间内股票价格，计算通过买入卖出可获得的最大收益。

输入一个大小为 n 的数 price(p1,p2,p3,p4…….pn),pi 是第i天的股票价格。

pi 的格式为股票价格(非负整型)加上货币单位 Y 或者 S,其中 Y 代表人民币,S 代表美元,这里规定 1 美元可以兑换 7 人民币。

Pi 样例 1：123Y 代表 123 元人民币

pi 样例 2：123S 代表 123 元美元,可兑换 861 人民币。

假设你可以在任何一天买入或者卖出股票,也可以选择放弃交易,请计其在交易周期 n 天内你能获得的最大收(以人民币计算)。

输入描述

输入一个包含交易周期内各天股票价格的字符串，以空格分隔。不考虑输入异常情况。

输出描述

输出一个整型数代表在交易周期 n 天内你能获得的最大收益，n 不能超过 10000

备注：股票价格只会用 Y 人民币或 S 美元进行输入，不考虑其他情况。

用例

输入	2Y 3S 4S 6Y 8S
输出	76
说明	无

题目解析

本题其实少了一句话，那就是，手上只能保留一只股票，不能保留多只股票。

如果可以保留多只股票，则用例2Y 3S 4S 6Y 8S，我前四个全要，即有四只股票，然后全部以8S价格卖出，那么最大利润为 8S * 4 - (2Y + 3S + 4S + 6Y) = 167，而不是76。

用例中的76输出，前提是手上只能保留一只股票。

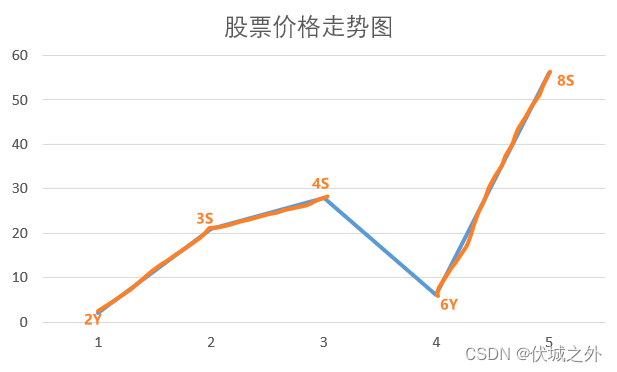
即：

2Y买进，3S卖出，赚19

3S买进，4S卖出，赚7

6Y买进，8S卖出，赚50

共转76

这是一种贪心思维，即买涨不买跌，这样就稳赚不赔了。如上折线图，只买上升区段，不买下跌区段。

本题和LeetCode - 122 买卖股票的最佳时机 II_伏城之外的博客-CSDN博客

相同，题解请看链接博客说明。

算法源码

/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");

const rl = readline.createInterface({
  input: process.stdin,
  output: process.stdout,
});

rl.on("line", (line) => {
  const arr = line.split(" ").map((price) => {
    const num = parseInt(price.substring(0, price.length - 1));
    return price.at(-1) === "Y" ? num : num * 7;
  });

  console.log(getResult(arr));
});

function getResult(arr) {
  let ans = 0;
  for (let i = 1; i < arr.length; i++) {
    ans += Math.max(0, arr[i] - arr[i - 1]);
  }
  return ans;
}