在数据建模流程中，都会涉及一个样本特征的相关性的分析，这个是建模流程中重要一环。通过量化特征字段之间的相关程度，可以将其作为一个重要信息维度，便于我们对模型训练的特征变量池进行有效筛选，不仅有简化模型且保证模型区分度与稳定性的作用，而且还可以明显提升数据建模任务的综合效率。今天我们会基于贷中存量客群的场景，讲讲相关性的相关实操内容。
根据特征分布类型与取值情况的差异，可以采用不同的处理方法来分析不同场景下的特征相关性能，例如pearson系数、spearman系数、卡方检验、方差分析等，具体情况如图1所示。由图可知，针对不同特征的取值类型，采用相应的处理方法是数据本身的信息价值，也是实际业务的场景需要，这样才能有效挖掘出样本特征隐藏的规律。
​
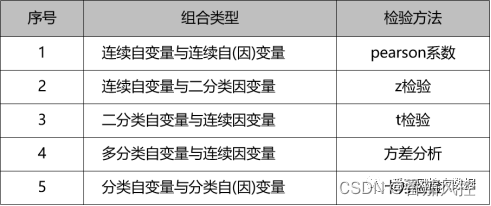
图1 不同特征类型的相关性评估

在以上列出的特征相关性分析方法中，pearson相关系数是最常用的一种量化方式。针对数值型变量，无论是连续型或离散型，还是float型或int型，都可以快速分析得到特征之间的pearson系数，从而根据绝对值越大相关性越强的规律，来研究特征变量的相关性分布。虽然pearson系数可以适用于所有数值型变量，但严格来讲，此系数主要是围绕连续型特征来展开分析的，而且是衡量特征线性关系的，并不能完全说明特征之间的真实相关程度。
举个例子，某两个特征变量的pearson系数为0，不能直接证明二者数据分布不相关，仅能体现出数据分布的线性不相关，可能非线性相关程度较强。若此时只根据pearson系数为0的结果将特征删除，在实际业务中显然是不合理的，对于有监督的机器学习模型来说，并未要求特征变量与目标变量必须是线性相关性要强，而是彼此相关性要强。因此，如何避免pearson相关系数在特征筛选阶段存在的缺陷，是我们在日常建模过程中需要特别注意的环节。结合以上情况，本文将给大家介绍另外一种特征相关性分析方法，与pearson相关系数来协同配合使用，那就是特征之间的距离distance相关系数。
1、Distance相关系数原理
距离distance相关系数可以衡量特征数据之间的非线性相关程度，可以解决pearson系数仅能量化数据线性相关的弱点。简单来讲，当两个特征变量的pearson相关系数为0时，不能说明二者的数据分布独立，但当distance相关系数为0时，必然证明二者分布彼此独立。特征distance相关系数的结果取值越大，说明特征变量之间的非线性相关程度越强。
特征的距离distance相关系数的计算，需要依赖于特征变量的距离协方差与距离方差，实现过程主要包括以下几个步骤：
（1）算出特征数组每行数据之间的范数距离；
（2）对所有的成对距离进行中心化处理；
（3）算出样本距离的平方协方差（标量）的算数平均样本距离方差；
（4）将两个随机变量的距离协方差除以它们的距离标准差的乘积，得到它们的距离相关性系数。

2、距离相关系数的实现
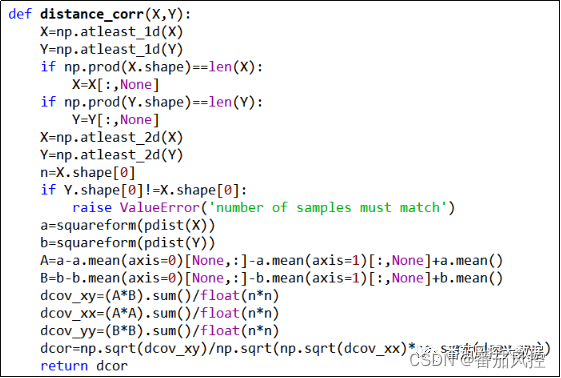
特征之间的距离distance相关系数，可以根据知识星球代码详情的自定义函数来实现，只需在函数distance_corr(X,Y)中指定输入两个特征数据X与Y，便可以直接输出二者的距离相关系数dcorr，从而按照取值越大则非线性相关性越强的规律，来评价特征变量之间的相关程度。
假如现有特征a（[3,1,8,0,6]）与特征b（[1,0,1,1,0]），调用以上distance_corr()函数可以得到特征a与b的距离相关系数0.1，同时我们采用corr()函数来输出二者的pearson系数，结果取值为0.2，具体实现过程如图3所示，可见这两个特征数据分布的非线性相关性与线性相关性存在着较明显的差异，仅通过单个系数来评价特征之间的相关程度是片面的。因此，我们在场景实践中，有必要对两种系数代表的相关性含义进行综合分析。

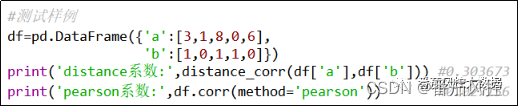
图3 特征距离相关系数举例

3、客户价值模型场景实践
为了便于大家更深入理解特征距离distance相关系数在实际场景中的应用，接下来我们围绕具体的场景案例数据，来介绍特征distance距离相关系数对特征筛选的参考意义，以及对模型拟合效果的影响分析。
3.1 实例样本数据
本文选取的样本数据包含5000条样本与6个字段，部分数据样例如图4所示。其中，id为样本主键，air_travel（航旅出行次数）、credit_use（信用卡使用次数）、stable_index（稳定性系数）、risk_score（风险评分）为特征变量，online_level（网购价值等级）为目标变量，取值1/0分别代表是否价值用户。样本数据的简单描述性统计分析EDA结果如图5所示，可见各特征无缺失值、异常值等情况。
​
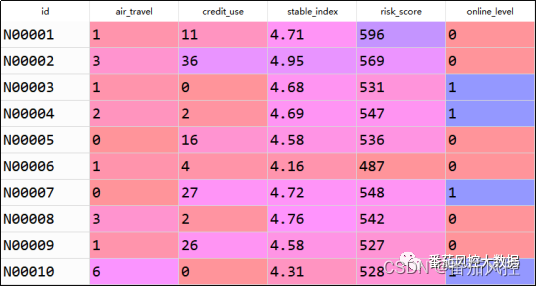
图4 样本数据样例

​
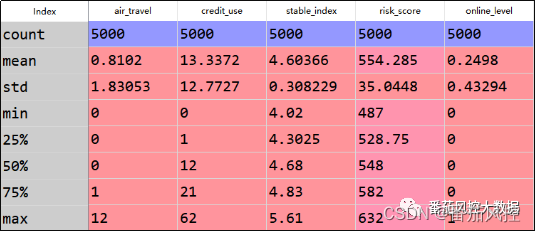
图5 样本EDA分布

本例建模目的是通过特征变量这4个信息维度，来对目标变量进行训练拟合。在模型训练之前，为了有效提升模型拟合效果，根据建模样本的数据分布情况，有必要采用特征工程的相关方法来对特征字段进行筛选。由于本文重点介绍特征相关性的内容，因此我们通过分析特征变量与目标变量的相关性，来衡量特征变量对模型目标的贡献价值。

3.2 根据相关系数筛选特征
根据实例样本数据，我们首先采用corr_p=data.drop(columns=[‘id’]).corr()来输出特征之间的pearson相关系数。在Python环境中，corr()默认method=‘pearson’，若需要生成spearman系数，则需要指定method=‘spearman’。根据以上简单逻辑，得到特征pearson相关系数的分布结果如图6所示。
​
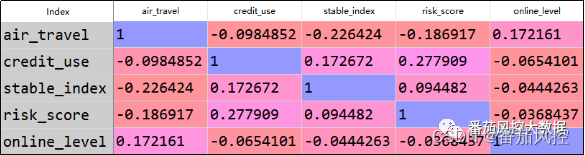
图6 特征pearson相关系数

通过以上结果可以看出，针对模型目标变量online_level，各特征变量与之线性相关程度由高到低的顺序依次为air_travel、credit_use、stable_index、risk_score，系数绝对值越大，说明彼此线性相关性越强，正值代表正相关，负值代表负相关。通过pearson相关系数的维度分析，可以判断特征risk_score对模型目标的贡献度最差，若采用特征筛选方式来简化模型，可优先考虑删除特征risk_score。
我们再来根据图2的特征距离相关系数的实现过程，来输出各特征变量与目标变量的特征distance距离相关系数。以特征air_travel为例，与目标online_level的距离系数实现过程为distance_corr(data[‘online_level’],data[‘air_travel’])，其他特征与之同理，最后汇总结果如图7所示。
​
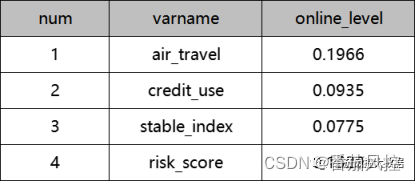
图7 特征distance相关系数

由以上结果可知，针对模型目标变量online_level，各特征变量与之非线性相关程度由高到低的顺序依次为air_travel、risk_score、credit_use、stable_index，系数取值越大，说明彼此非线性相关性越强。通过distance相关系数的维度分析，可以判断特征stable_index对模型目标的贡献度最差，若采用特征筛选方式来简化模型，可优先考虑删除特征stable_index，这个分析结果显然与前边pearson系数是不同的。
在pearson系数分布中，特征risk_score与目标变量online_level的相关程度是最弱的（-0.0368437），且与最强变量air_travel表现（0.172161）的量化差距是很大的。但是，在distance系数分布中，特征risk_score与目标变量online_level的相关程度不仅非最弱（0.1629），且与最强变量air_travel表现（0.1966）的量化结果是很接近的。从这个分析结果可知，在衡量特征变量对目标变量的相关程度时，不能仅依据其中某一个相关系数维度来评价，而是要综合性分析，毕竟线性相关与非线性相关所体现的数据规律是完全不同的。
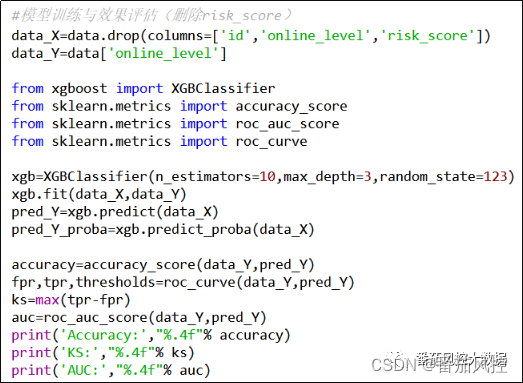
以上两种不同维度的相关性分析方法，对特征筛选的策略实施有不同的结果，为了进一步证明二者对模型拟合效果有较大影响，我们在特征pearson线性相关系数和distance非线性相关系数情况下，分别训练拟合模型，并通过模型的常见指标来进行评价。这里采用XGBoost分类算法来构建模型，第1种情况为根据pearson系数结果删除特征risk_score，第2种情况为根据distance系数结果删除特征stable_index，对应的模型训练与模型评估过程详见知识星球代码详情。此外，为了实现模型性能的横向对比，模型训练参数均保持统一。
通过变量pearson系数和distance系数两种特征筛选情况下的模型拟合训练，选取二分类模型常用的模型指标Accuray、KS、AUC来评价模型综合性能，具体指标结果如图10所示。
​
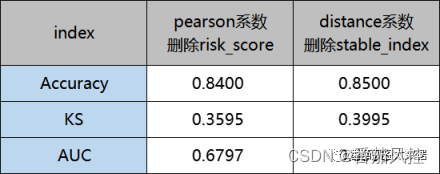
图10 模型效果指标对比

由以上模型结果可知，通过pearson相关系数删除特征risk_score，以及distance相关系数删除特征stable_index的模型评估指标，存在较明显的差异，尤其是分类模型典型的区分度指标KS，二者表现（0.3595、0.3995）有一定的差距。因此，通过以上分析，我们可以清晰的了解到，根据特征相关性来筛选特征变量时，由于pearson系数与distance系数量化的信息维度不同，对应的模型效果也是有很大区别的。
在实际建模场景中，我们需要明确，若希望较准确的评估特征变量之间的相关性，并以此来进行特征筛选时，更为全面的思路是同时兼顾pearson线性相关系数与distance非线性相关系数的分布情况，这样分析得到的特征相关程度认定，以及特征变量筛选结果，对特征数据分析或样本数据建模的效果更为合理。例如本例的特征筛选环节，特征变量stable_index与目标变量online_level的相关性评估，在pearson线性相关与distance非线性相关两方面均表现较差，应优先考虑将其删除，而且其模型效果也反映了这个策略的准确性。
综合以上内容，我们介绍了特征距离distance相关系数的理论价值与实践意义，并围绕实例样本数据，完成了特征distance非线性相关系数与pearson线性相关系数的完美结合应用。
为了便于大家对以上内容的进一步理解与熟悉，本文额外附带了与此同步的Python代码与样本数据，详情请移至知识星球参考相关内容：
​

…

~原创文章