一、决策树
1、什么是决策树?如何进行高效的决策?
最早的决策树就是利用程序设计中的if-else结构分割数据的一种分类学习法。决策树的思想就是:如何高效的进行决策。而我们决策是有顺序的,即:我们在看不同的特征的时候,先看哪一个,后看哪一个是有讲究的。因为正确的特征先后顺序有利于我们进行高效的决策。比如:
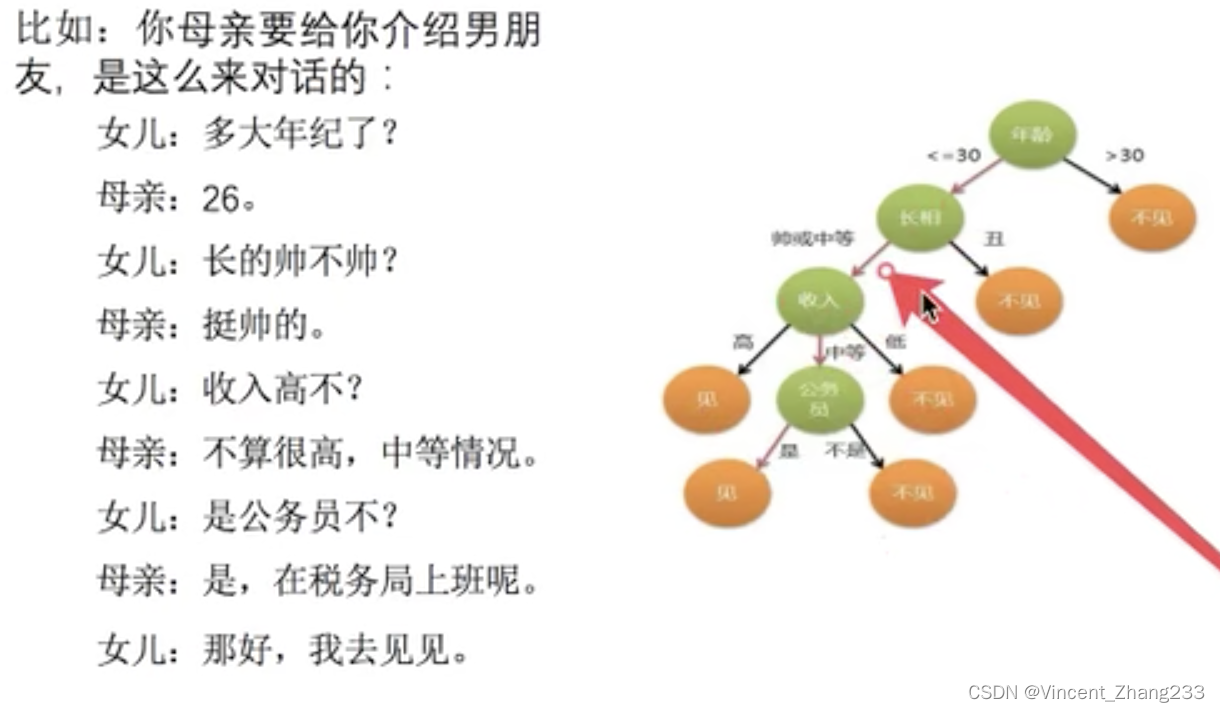
从上图可以看出,该女生最在意的是男方的年龄,其次是长相,收入,职业。如果男方年龄不合适,则直接就不见了,就省去了后面的问题。所以正确的特征的先后顺序有利于我们进行高效决策。
2、特征的先后顺序
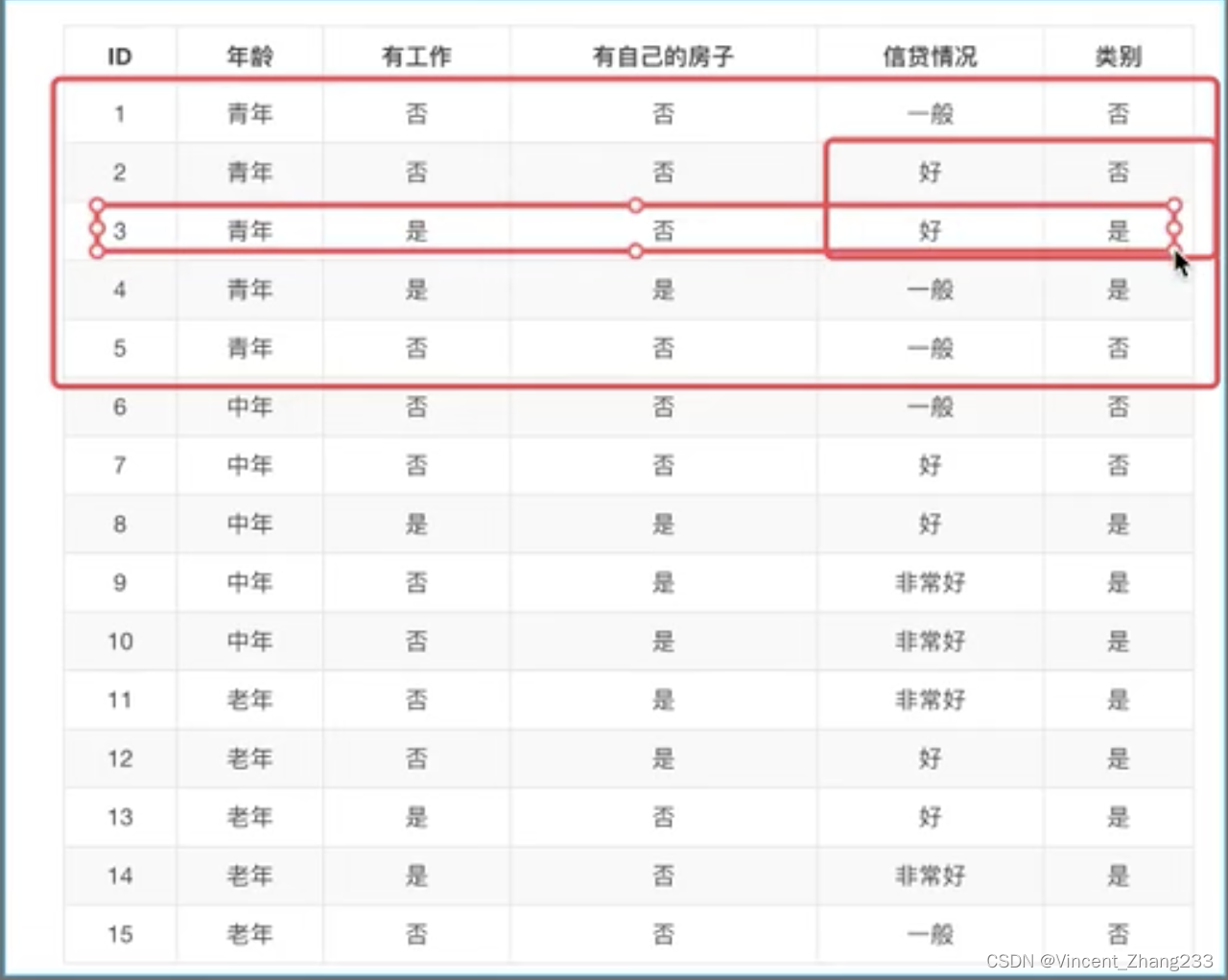
举例:已知有四个特征:“年龄”,“是否有工作”,“是否有自己的房子”,“信贷情况”这四个特征,请你预测是否要贷款给某个人。
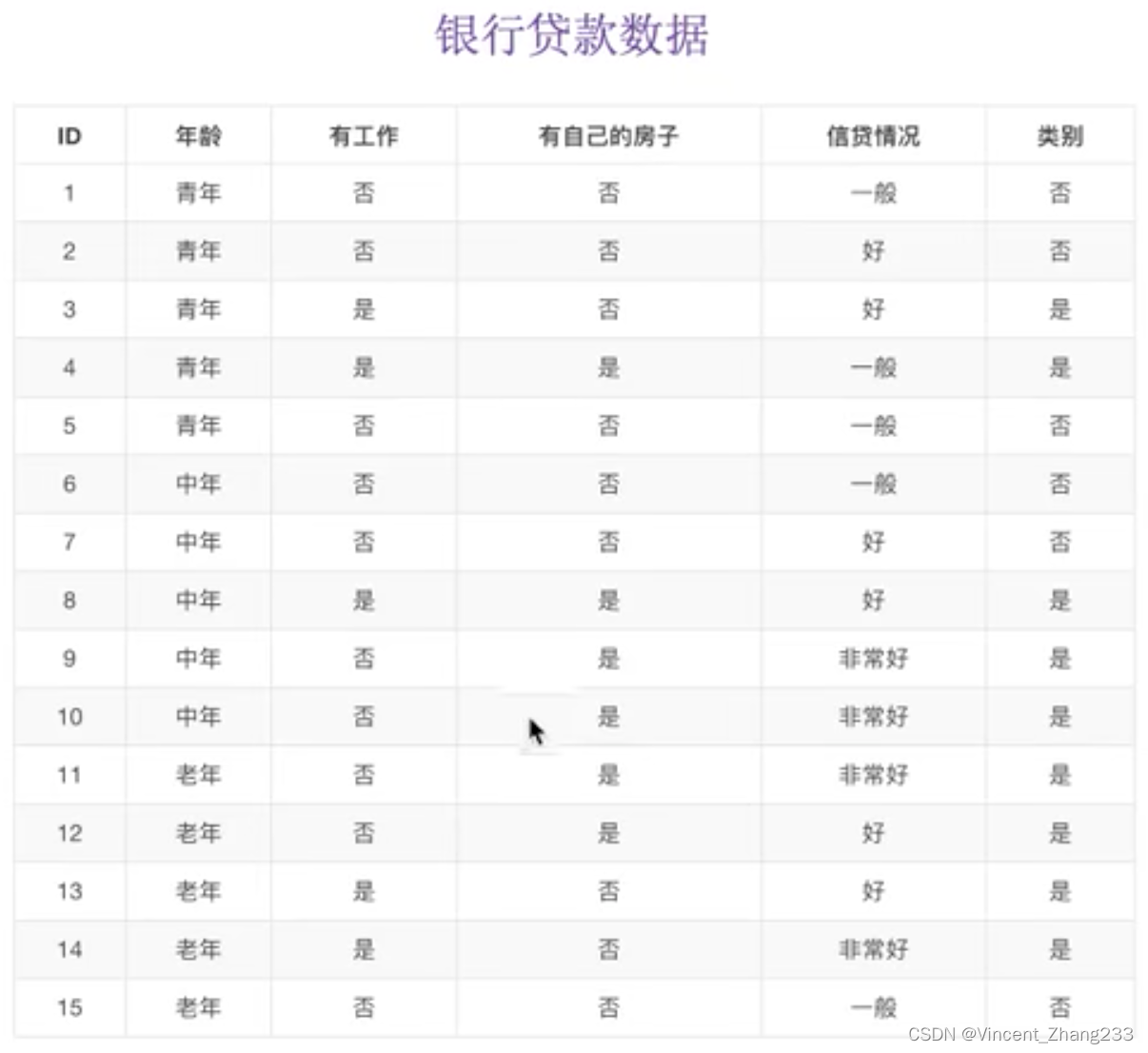
参考上图(以往的样本),如果我们先看是否有房子,再看是否有工作:
以往的样本中,有房子的都拿到了贷款:
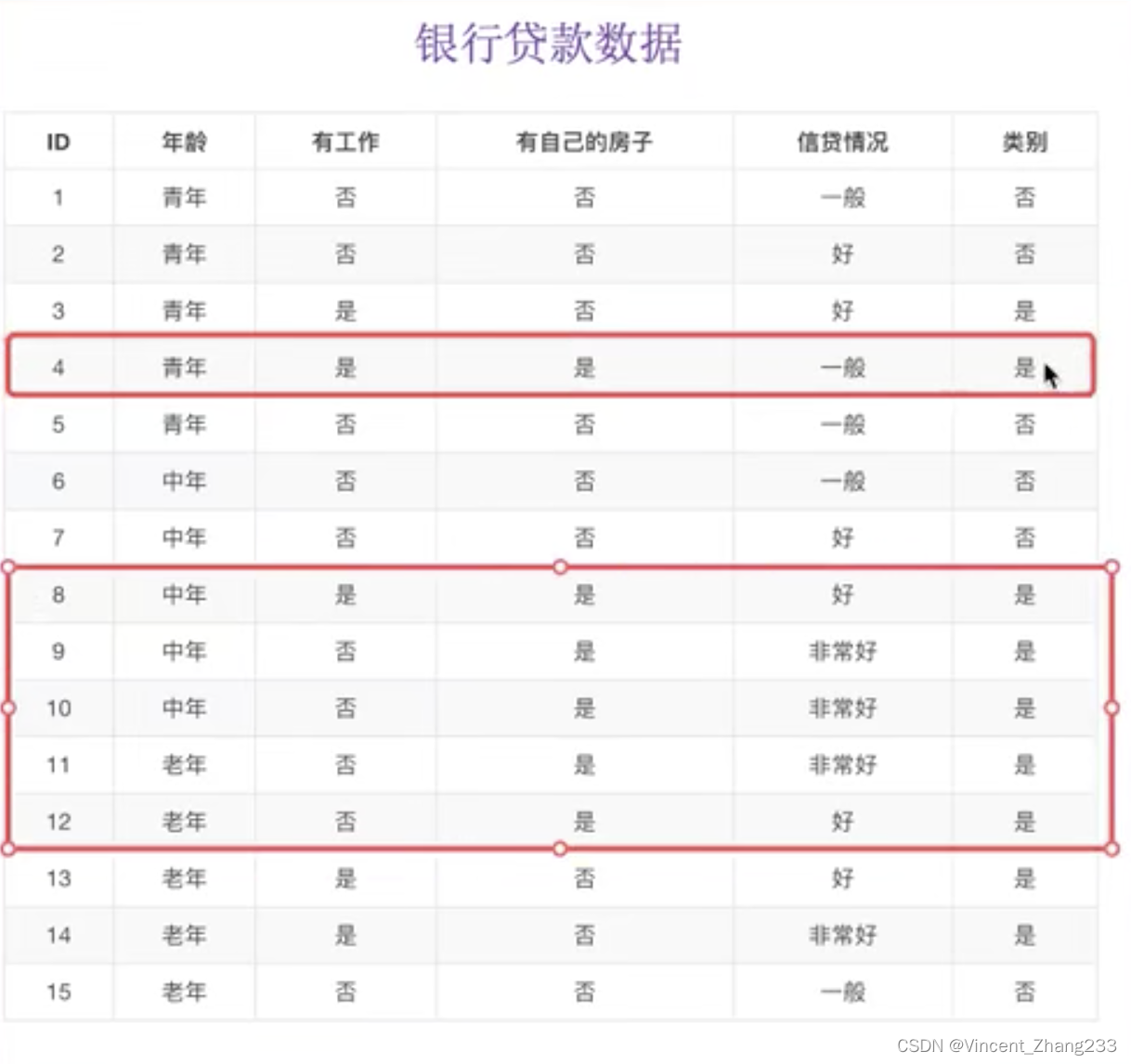
但是,有一些人没有房子也拿到了贷款,所以我们光看房子还不够,所以继续看是否有工作。
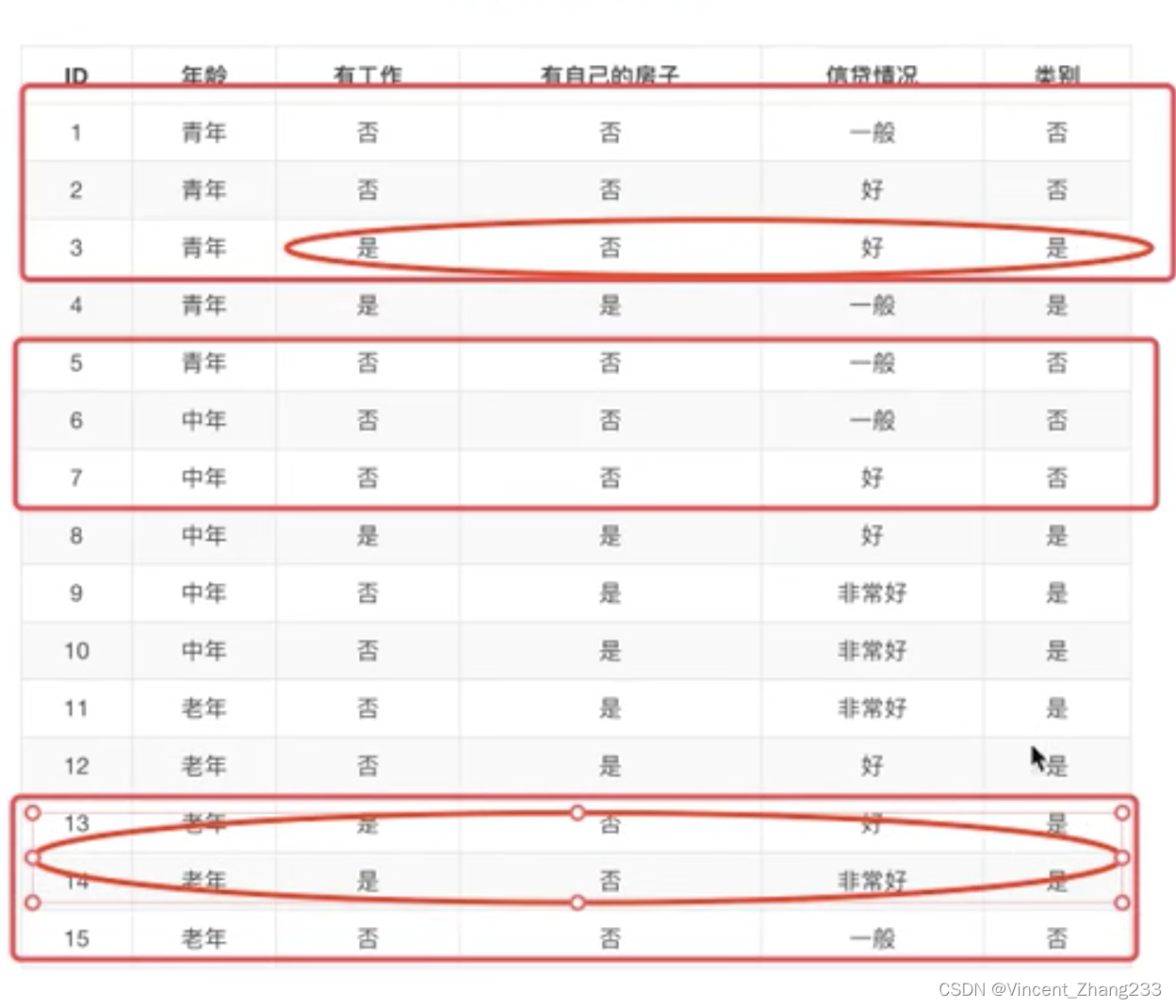
剩下的没放没工作的人,不论信用如何,都没有拿到贷款。所以如果我们先看房子,再看工作,就不用再看其他特征,就可以决定是否贷款了。
如果我们不按照这个顺序,比如我们先看年龄,再看信贷情况,再看工作,才能确定是否贷款。如下图:
我们需要看3个特征才能确定是否贷款,这个效率显然就比前面看2个特征的效率要低了。所以,特征的先后顺序会影响到我们决策的效率。
那么问题来了,我们如何找到高效的决策顺序呢?这里就要引入信息熵、信息增益的知识。
3、信息论基础——信息熵
1)什么是信息?
信息是消除随机不定性的东西是信息(香农定义的)。比如:我不确定小明的年龄。而小明说:“我今年18岁。”那么“我今年18岁。”就是一个信息。
为了进一步取理解什么是信息,我们再举一个例子:现在我已经知道小明18岁了,而小华说:“小明明年19岁。”那么“小明明年19岁。”这句话就不算信息了,因为小明之前已经告诉了我他的年龄,我对于小明年龄的不确定性已经被消除,所以小华这句话并没有消除我任何不确定性,所以不能算是信息。
2)信息的衡量——信息量和信息熵
信息熵并不直接等于信息量(很多人错误地以为信息熵=信息量,其实并不是!!!)
在信息论中,信息熵度量的是一条信息的不确定程度,不确定性越大,则信息熵越大
那么如何衡量我消除不确定性的大小呢?这需要我们去对信息进行量化,从而产生了一个新名词——信息熵,就是我们消除不确定性的大小