Abstract
通过似然热图对输出分布进行建模的基于热图的方法在人体姿态估计领域占据主导地位。相比之下，基于回归的方法更有效，但效果较差。 在这项工作中，我们探索了最大似然估计（MLE），以开发一种高效有效的基于回归的方法。从MLE的角度来看，采用不同的回归损失是对输出密度函数做出不同的假设。密度函数越接近真实分布，回归性能越好。有鉴于此，我们提出了一种新的残差对数似然回归范式估计（RLE），以捕获潜在的输出分布。具体来说，RLE学习分布的变化，而不是未引用的底层分布，以促进训练过程。通过所提出的重新参数化设计，我们的方法与现成的流动模型兼容。所提出的方法是有效的、高效的和灵活的。我们通过综合实验展示了它在各种人体姿态估计任务中的潜力。与传统的回归范式相比，RLE回归在没有任何测试时间开销的情况下，使MSCOCO提高了12.4mAP。此外，我们的回归方法首次优于基于热图的方法，尤其是在多人姿态估计方面。我们的代码可在https://github.com/Jeff-sjtu/resloglikelihood-regression
1. Introduction
人体姿态估计在计算机视觉领域得到了广泛的研究[23，24，1，32，21]。最近，随着深度卷积神经网络的发展，已经取得了重大进展。现有的方法可分为两类：基于热图的[60，59，65，4，67，57，49，55]和基于回归的[61，5，56，73，45，64]。这些方法展示了绘制每个关节的热图，并使用argmax[59，67，49]或软argmax[43，34，57]操作将关节定位为点的可能性。尽管具有优异的性能，但基于热图的方法仍存在较高的计算和存储需求。将热图扩展到3D或4D（空间+时间）将是昂贵的。此外，很难用现代单阶段方法部署热图
基于回归的方法直接将输入映射到输出关节坐标，这对于各种人体姿态估计任务和实时应用来说是灵活高效的，尤其是在终端设备上。标准热图头（3个去卷积层）的成本为ResNet-50主干的1.4×FLOP，而回归头的成本仅为相同主干的1/20000 FLOP。然而，回归表现不佳。在具有挑战性的情况下，如遮挡、运动模糊和截断，基本事实标签本质上是模糊的。基于热图的方法对于
通过利用可能性热图来消除这些模糊性。但目前的回归方法很容易受到这些嘈杂标签的影响。
……介绍省略
3. Method
在这项工作中，我们的目标是将基于回归的方法的性能提高到基于热图的方法的竞争水平。与基于热图的方法相比，基于回归的方法有很多优点：i）摆脱了高分辨率热图，并且具有较低的计算和存储复杂性。ii）它具有连续输出，不存在量化问题。iii）它可以以最小的成本扩展到各种场景（例如，单阶段方法、基于视频的方法、3D场景）。然而，现有的基于回归的方法性能较差，这是致命的，并限制了其广泛使用。
在本节中，在介绍我们的解决方案之前，我们首先从§3.1中的最大似然估计的角度回顾了回归的一般公式。然后，在§3.2中，我们提出了残差对数似然估计（RLE），这是一种利用归一化流来捕获潜在的残差对数似然函数并促进人体姿态回归的方法。最后，§3.3中提供了必要的实施细节。
3.1. General Formulation of Regression
标准的回归范式是将L1或L2损失应用于回归输出
。损失函数是根据经验，为不同的任务选择的。在这里，我们从最大似然估计的角度来回顾回归问题。给定输入图像
，回归模型预测分布
，该分布指示gt真值出现在位置x的概率，其中θ表示可学习的模型参数。
由于标签中固有的模糊性，标记位置
是标注人员人为标注的结果。学习过程是优化模型参数θ，使观察到的标签最有可能出现。因此，损失函数该最大似然估计（MLE）过程的最大似然估计被定义为：
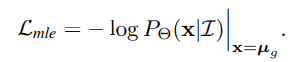
在这个公式中，不同的回归损失本质上是输出概率分布的不同假设。例如，在物体检测[18，29，28]和密集对应[40]的一些工作中，假设密度是高斯分布。该模型需要预测两个值，
，以构建密度函数
。为了最大化观察到的标签
的可能性，损失函数变为：
如果我们假设密度函数具有常数方差，即
是常数，则损失函数退化为标准的L2损耗：
此外，如果我们假设密度遵循具有恒定方差的拉普拉斯分布，则损失函数成为标准的L1损失”。在推理阶段，
用于控制分布位置的值，用作回归输出。
从这个角度来看，损失函数取决于分布
的形状。因此，更精确的密度函数可以产生更好的结果。然而，由于潜在分布的分析表达式是未知的，该模型不能简单地回归几个值来构建密度函数，如方程2。为了估计潜在分布并促进人体姿势回归，在下一节中，我们通过利用归一化流提出了一种新的回归范式。
3.2. Regression with Normalizing Flows
在本小节中，我们介绍了所提出的范式的三种变体，它们利用归一化流进行回归（见图2）。
Basic Design.
所提出的具有归一化流的回归范式的基本设计如图所示。
第2（a）段。这里，归一化流[52，11，26，46，25]学习 通过可逆映射变换简单分布来构造复杂分布。我们考虑随机变量z上的分布
作为初始密度函数。它是由回归模型Θ的输出
定义的。为了简单起见，我们假设
即高斯分布。一个光滑且可逆的映射
将z变换为x，即
，其中φ是流模型的可学习参数。
变换后的变量x遵循另一个分布
。概率密度函数
取决于回归模型θ和流量模型fφ，可以计算为：
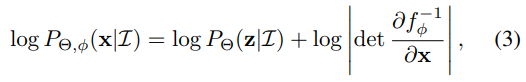
其中
是的倒数，
。这样，给定任意x，可以通过方程3通过反向计算z来估计相应的对数概率。此外，
是可学习的，并且只要
足够复杂，就可以拟合任意分布。在实践中，我们可以通过组合多个简单的映射来成功的表达一个负责的函数，即
对学习的分布
执行最大似然过程。因此，损失函数公式化为：
请注意，潜在的最优分布
是未知的。流模型通过最大化标记位置的可能性以无监督的方式学习。例如，具有挑战性的情况（例如，cclusions），对于标注者的标签偏差较大的，预测的分布应该具有较大的方差，以最大化对数概率。
Reparameterization.
虽然基本设计看起来合理，但在实践中并不可行。的学习，依赖于损失函数中的
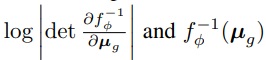。因此，φ将学会跨越所有图像拟合
（真值）的分布。然而，我们想要了解的分布是关于输出如何偏离对输入图像的基本事实条件，而不是基本事实本身在所有图像中的分布。
在这里，为了使我们的回归框架可行并与现成的流模型兼容，我们进一步设计了具有重新参数化策略的回归范式。新的范例如图2（b）所示。我们假设所有潜在分布共享相同的密度函数族，但在输入
上具有不同的均值和方差条件。首先，利用流量模型fφ来映射零均值初始分布
到零平均变形分布
。然后，回归模型Θ预测两个值，，以控制分布的位置和规模。通过将x移动和重新缩放到
来获得最终分布
，其中
因此，具有重新参数化的损失函数可以写成：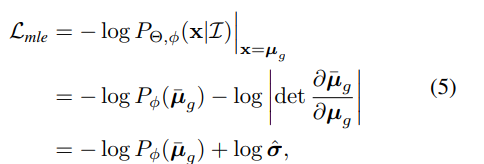
式中，
通过重新参数化设计，现在流量模型可以专注于学习
的分布，这反映了输出与真值的偏差。
Residual Log-likelihood Estimation.
残差对数似然估计。在重新参数化之后，可以以端到端的方式训练回归框架。根据损失函数中的项
，回归值的训练
和流量模型
耦合在一起（等式5）。然而，这两个模型之间存在着复杂的依赖关系。回归模型的训练完全依赖于流量模型
估计的分布。在训练的初始阶段，分布的形状远远不正确，这增加了训练回归模型的难度，并可能降低模型的性能。
为了便于训练过程，我们开发了一种gradient shortcut来减少这两个模型之间的依赖性。形式上，由流动模型
估计的分布试图拟合最优的基本分布
，它可以分为三项：
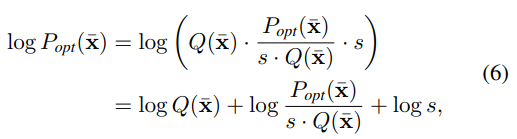
其中，项Q（x）可以是一个简单的分布，例如高斯分布
，
是我们所说的残差对数似然，常数s是为了确保残差项是一个分布。我们假设
可以大致匹配基本分布，但不能完全匹配。剩余对数似然是为了补偿差异。因此，我们以与等式6相同的方式划分
的对数概率：
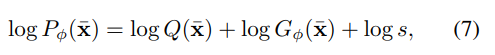
其中
是通过流模型学习的分布。
的值可以用
来近似。s的推导见补充文件。
通过这种方式，Gφ（x）将试图拟合潜在的残差似然
，而不是学习整个分布。最后，结合重新参数化设计（等式5）和残差对数似然估计（等式7），总损失函数可以定义为：
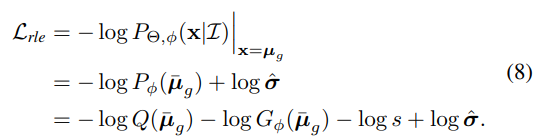
这个过程如图所示。在训练过程中，来自
的反向传播梯度不依赖于流模型，这加速了回归模型的训练。此外，正如ResNet[16]的假设，优化残差映射比优化原始未引用映射更容易。
在极端情况下，如果预设近似
是最优的，那么将残差对数概率推至零比通过fφ中的可逆映射堆栈拟合恒等映射更容易。残差对数似然估计的有效性在§4.1中得到验证
3.3. Implementation Details
在训练阶段，以端到端的方式同时优化回归模型和流模型。我们将标准回归损失L1和L2替换为所提出的残差对数似然估计损失
。默认初始密度设置为拉普拉斯分布。在测试阶段，预测的平均值
作为回归输出。因此，在推理过程中不需要运行流模型。这一特性使得所提出的方法灵活且易于应用于各种回归算法，而没有任何测试时间开销。此外，预测置信度可以从
其中，是第i个关节的学习偏差，K表示关节的总数。用sigmoid型函数预测偏差
。因此，我们有
Flow Model.
所提出的回归范式对流量模型是不可知的。因此，可以应用各种现成的流量模型[52，11，26，46，25]。在实验中，我们采用RealNVP[11]进行快速训练。我们将具有Nn个神经元的Lfc完全连接层的可逆函数表示为Lfc×Nn。默认情况下，我们设置Lfc=3和Nn=64。流模型是轻量级的，几乎不会影响训练速度。补充文件（§A）中提供了流模型体系结构和更多细节。
Task
所提出的回归范式是通用的，可以用于各种人体姿态估计任务。在实验中，我们在五项任务中的七种不同算法上验证了所提出的回归范式：单人2D姿势估计、自上而下的2D姿势估计和一阶段
2D姿态估计、单阶段3D姿态估计和两阶段3D姿态评估。§4和§5提供了详细的培训设置。补充文件中提供了关于单人2D姿势估计的实验。
