基于逻辑回归对股票客户流失预测分析

作者：i阿极

作者简介：Python领域新星作者、多项比赛获奖者：博主个人首页

😊😊😊如果觉得文章不错或能帮助到你学习，可以点赞👍收藏📁评论📒+关注哦！👍👍👍

📜📜📜如果有小伙伴需要数据集和学习交流，文章下方有交流学习区！一起学习进步！💪

---

专栏案例：机器学习案例
机器学习(一)：线性回归之最小二乘法
机器学习(二)：线性回归之梯度下降法
机器学习(三)：基于线性回归对波士顿房价预测
机器学习(四)：基于KNN算法对鸢尾花类别进行分类预测
机器学习(五)：基于KNN模型对高炉发电量进行回归预测分析
机器学习(六)：基于高斯贝叶斯对面部皮肤进行预测分析
机器学习(七)：基于多项式贝叶斯对蘑菇毒性分类预测分析
机器学习(十四)：基于逻辑回归对超市销售活动预测分析
机器学习(十五)：基于神经网络对用户评论情感分析预测
机器学习(十六)：线性回归分析女性身高与体重之间的关系
机器学习(十七)：基于支持向量机（SVM）进行人脸识别预测
机器学习(十八)：基于逻辑回归对优惠券使用情况预测分析
机器学习(十九）：基于逻辑回归对某银行客户违约预测分析
机器学习(二十)：基于朴素贝叶斯对花瓣花萼的宽度和长度分类预测
机器学习(二十一)：LightGBM算法原理（附案例实战）

---

---

1、逻辑回归模型原理

逻辑回归（Logistic Regression）是一种二分类的监督学习算法，用于预测样本的概率属于某一类别的概率。相比于线性回归，逻辑回归可以更好地处理分类问题。

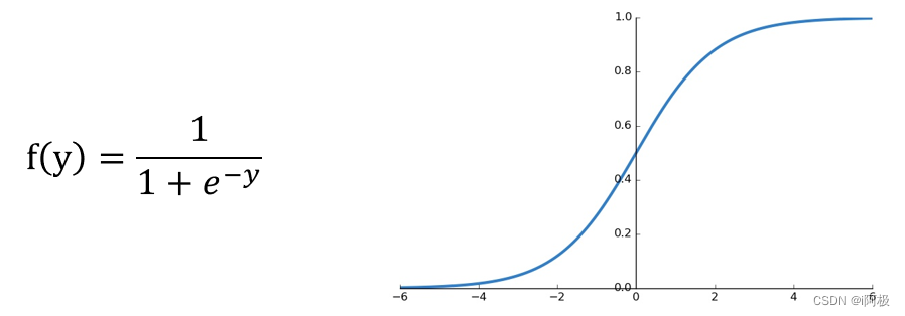
逻辑回归的核心思想是，通过对样本特征进行线性组合，得到一个连续的预测值，然后通过一个函数将其映射到0和1之间的概率值。这个映射函数通常采用Sigmoid函数，其数学表达式为：

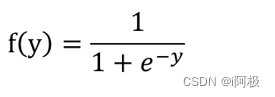
其中$y$为线性组合的结果，$e$为自然常数。

逻辑回归模型的数学表达式为：

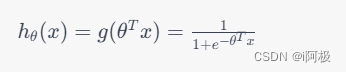
其中，$\theta$是需要学习的参数，$x$是输入的样本特征向量。

我们的目标是最大化训练样本的似然函数，即：

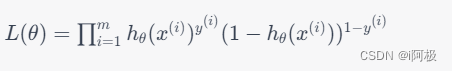
其中，$m$是训练样本数，$y^{(i)}$为样本$i$的真实标签。

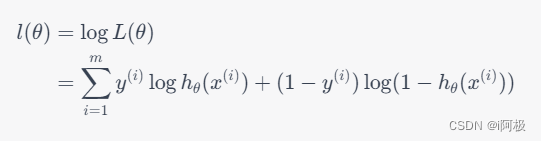
我们的目标是最大化对数似然函数，即：

可以使用梯度下降等优化算法来求解最优参数$\theta$。

逻辑回归的优点包括：

• 简单易懂，容易解释
• 计算量小，速度快
• 适用于线性可分和线性不可分的二分类问题

逻辑回归的缺点包括：

• 对异常值敏感
• 对特征相关性敏感
• 不能很好地处理多分类问题

2、实验环境

python 3.9

anaconda

jupyter notebook

3、模型LogisticRegression函数介绍

LogisticRegression(penalty='l2', dual=False, tol=0.0001, C=1.0, fit_intercept=True, intercept_scaling=1,
                               class_weight=None, random_state=None, solver= 'liblinear',max_iter=100, 
                               multi_class='ovr', verbose=0, warm_start=False, n_jobs=1)

• penalty：为Logistic回归模型的目标函数添加正则化惩罚项，与线性回归模型类似，默认为l2正则

• dual：bool类型参数，是否求解对偶形式，默认为False，只有当penalty参数为’l2’、solver参数为’liblinear’时，才可使用对偶形式

• tol：用于指定模型跌倒收敛的阈值

• C：用于指定惩罚项系数Lambda的倒数，值越小，正则化项越大

• fit_intercept：bool类型参数，是否拟合模型的截距项，默认为True

• intercept_scaling：当solver参数为’liblinear’时该参数有效，主要是为了降低X矩阵中人为设定的常数列1的影响

• class_weight：用于指定因变量类别的权重，如果为字典，则通过字典的形式{class_label:weight}传递每个类别的权重；如果为字符串’balanced’，则每个分类的权重与实际样本中的比例成反比，当各分类存在严重不平衡时，设置为’balanced’会比较好；如果为None，则表示每个分类的权重相等

• random_state：用于指定随机数生成器的种子

• solver：用于指定求解目标函数最优化的算法，默认为’liblinear’，还有其他选项，如牛顿法’newton-cg’、L-BFGS拟牛顿法’lbfgs’

• max_iter：指定模型求解过程中的最大迭代次数， 默认为100

• multi_class：如果因变量不止两个分类，可以通过该参数指定多分类问题的解决办法，默认采用’ovr’，即one-vs-rest方法，还可以指定’multinomial’，表示直接使用多分类逻辑回归模型（Softmax分类）

• verbose：bool类型参数，是否输出模型迭代过程的信息，默认为0，表示不输出

• warm_start：bool类型参数，是否基于上一次的训练结果继续训练模型，默认为False，表示每次迭代都是从头开始

• n_jobs：指定模型运算时使用的CPU数量，默认为1，如果为-1，表示使用所有可用的CPU

4、逻辑回归实战案例

4.1案例背景

在进行每一笔股票交易的时候，交易者（股民）都是要付给开户所在的证券公司一些手续费的，虽然单笔交易的手续费并不高，然而股票市场每日都有巨额的成交量，使得每一笔交易的手续费汇总起来的数目相当可观，而这一部分收入对于一些证券公司来说很重要，甚至可以占到所有营业收入50%以上，因此证券公司对于客户（也即交易者）的忠诚度和活跃度是很看重的。

如果一个客户不再通过该证券公司交易，也即该客户流失了，那么对于证券公司来说便损失了一个收入来源，因此证券公司会搭建一套客户流失预警模型来预测交易者是否会流失，从而对于流失概率较大的客户进行相应的挽回措施，因为通常情况下，获得新客户的成本比保留现有客户的成本要高的多。

4.2数据读取和数据集划分

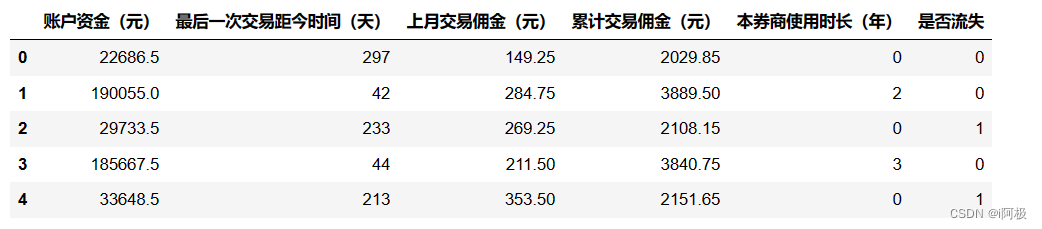
读取数据并展示前五行数据

import pandas as pd
df = pd.read_excel('股票客户流失.xlsx')
df.head()

划分特征变量和目标变量

X = df.drop(columns='是否流失') 
y = df['是否流失']   

划分训练集和测试集

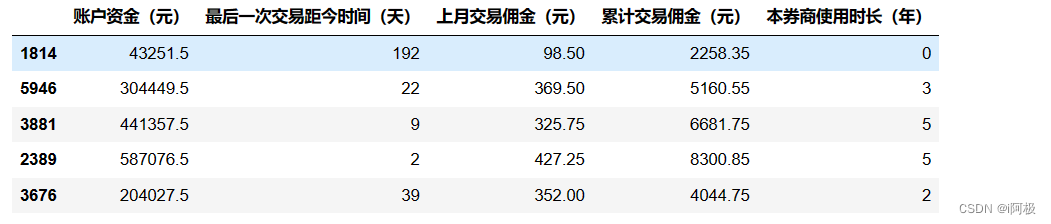
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1)  # 设置random_state使得每次划分的数据一样

X_train.head()  # 显示训练集X_train的前5行

4.3模型建立与预测评价

模型搭建

from sklearn.linear_model import LogisticRegression
model = LogisticRegression()
model.fit(X_train, y_train)

预测数据结果

y_pred = model.predict(X_test)
print(y_pred[0:100])  # 打印预测内容的前100个看看

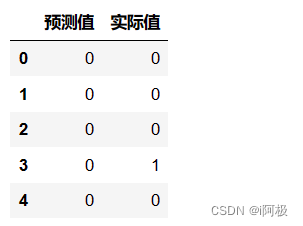
放到一个DataFrame里进行查看比对

a = pd.DataFrame()  # 创建一个空DataFrame 
a['预测值'] = list(y_pred)
a['实际值'] = list(y_test)
a.head()  # 可以看到此时前5个预测准确度为80%

看全部的预测准确度

from sklearn.metrics import accuracy_score
score = accuracy_score(y_pred, y_test)
print(score)

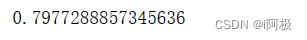
预测概率

y_pred_proba = model.predict_proba(X_test)  
y_pred_proba[0:5]

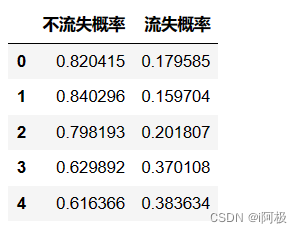
查看概率的方式

a = pd.DataFrame(y_pred_proba, columns=['不流失概率', '流失概率'])
a.head()

查看流失的概率

y_pred_proba[:,1]

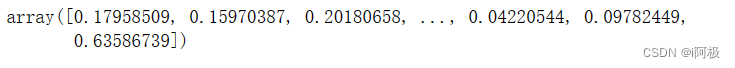
4.4绘制ROC曲线

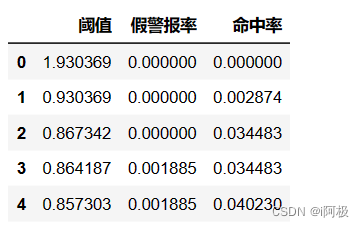
计算ROC曲线需要的假警报率（fpr）、命中率（tpr）及阈值（thres）

from sklearn.metrics import roc_curve
fpr, tpr, thres = roc_curve(y_test, y_pred_proba[:,1])
a = pd.DataFrame()  # 创建一个空DataFrame 
a['阈值'] = list(thres)
a['假警报率'] = list(fpr)
a['命中率'] = list(tpr)
a.head()

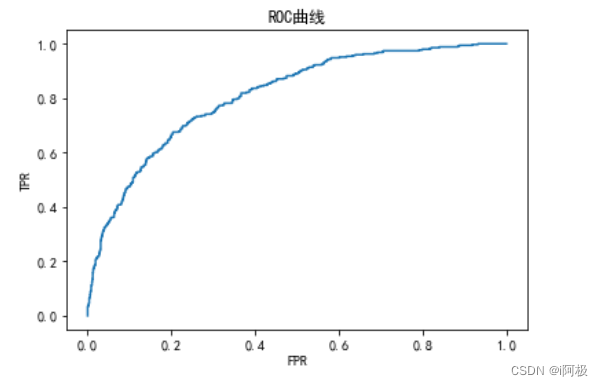
绘制ROC曲线

import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']  # 设置中文
plt.plot(fpr, tpr)  # 通过plot()函数绘制折线图
plt.title('ROC曲线')  # 添加标题，注意如果要写中文，需要在之前添加一行代码：plt.rcParams['font.sans-serif'] = ['SimHei']
plt.xlabel('FPR')  # 添加X轴标签
plt.ylabel('TPR')  # 添加Y轴标
plt.show()

求出模型的AUC值

from sklearn.metrics import roc_auc_score
score = roc_auc_score(y_test, y_pred_proba[:,1])
score

---

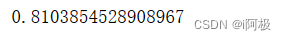
📢文章下方有交流学习区！一起学习进步！💪💪💪
📢首发CSDN博客，创作不易，如果觉得文章不错，可以点赞👍收藏📁评论📒
📢你的支持和鼓励是我创作的动力❗❗❗