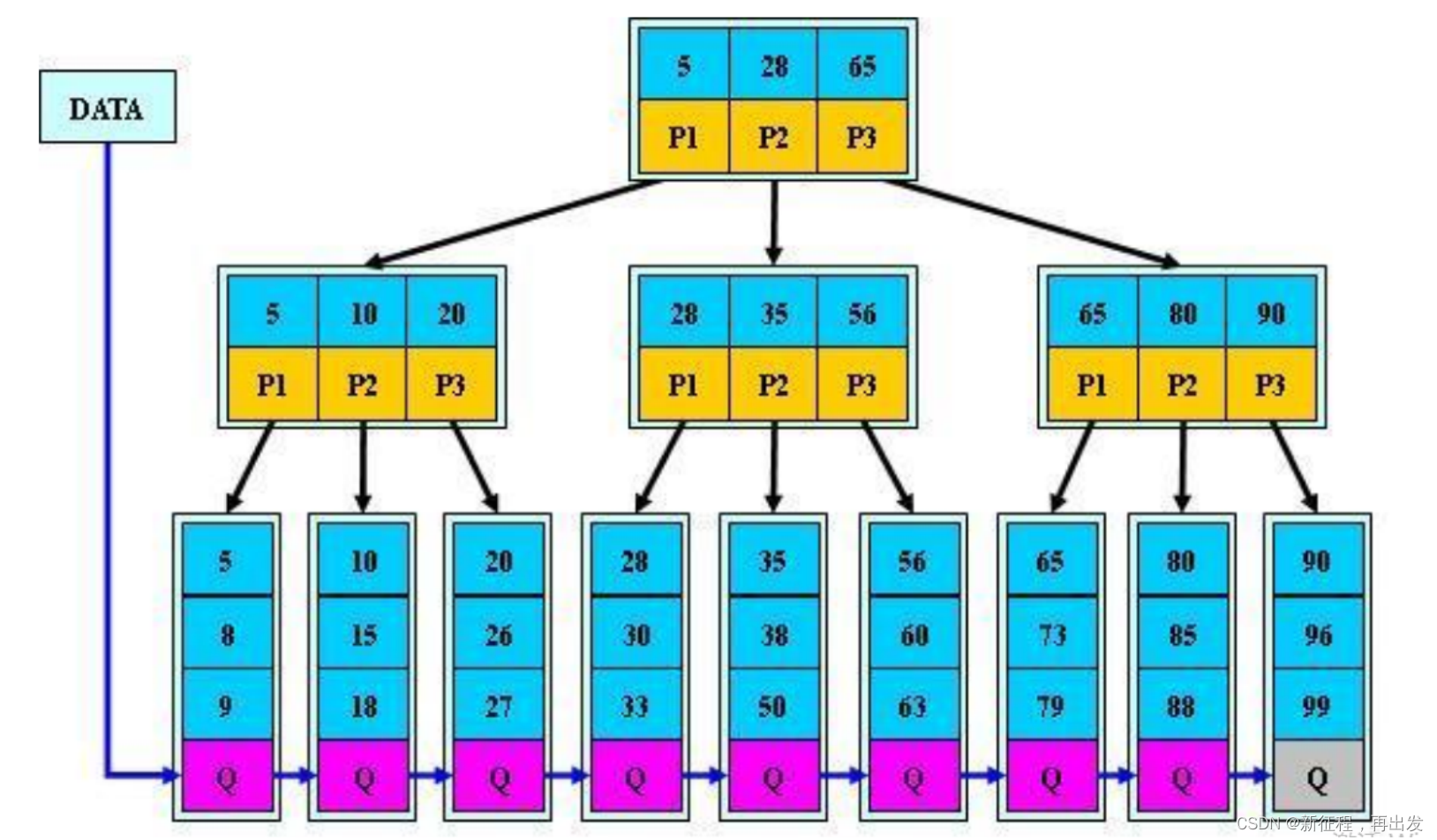
图神经网络模型介绍
- 将图神经网络分为基于谱域上的模型和基于空域上的模型,并按照发展顺序详解每个类别中的重要模型。
基于谱域的图神经网络
- 谱域上的图卷积在图学习迈向深度学习的发展历程上起到了关键性的作用。
- 三个具有代表性的谱域图神经网络
- 谱图卷积网络
- 切比雪夫网络和
- 图卷积网络
谱域卷积网络
在第一章中我们讲到,由于图的节点不均匀性、排列不变性、及额外边属性等。规则网络上的卷积网络不能直接应用到图中,那么,我们将如何定义图上的卷积呢?
图信号分析和图谱理论为我们提供了一个从谱域上进行卷积的操作。
卷积定理
函数卷积的傅里叶变换是函数傅里叶变换的乘积。即
F
(
f
∗
g
)
=
F
(
f
)
∗
F
(
g
)
=
f
^
∗
g
^
F(f * g) = F(f) * F(g) = \hat{f} * \hat{g}
F(f∗g)=F(f)∗F(g)=f^∗g^
其中
F
(
f
)
F(f)
F(f)表示
f
f
f的傅里叶变换得到对应的谱域信号
f
^
\hat{f}
f^
通过傅里叶逆变换
F
−
1
F^{-1}
F−1,可以得到如下卷积形式:
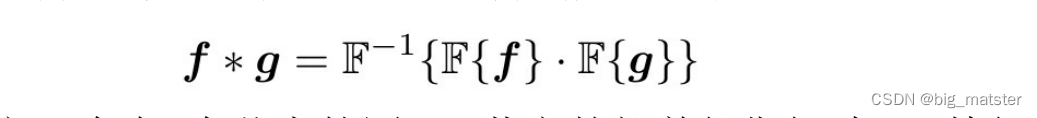

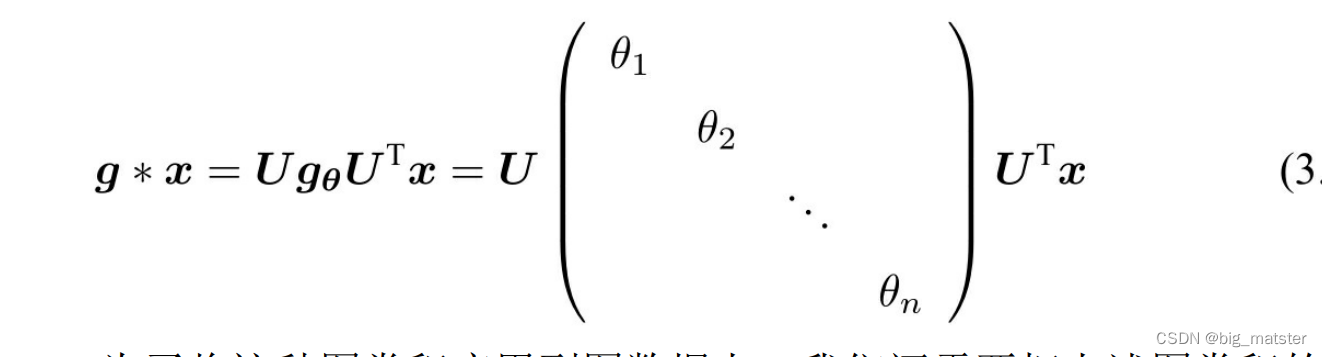
- 图信号 x x x与一个滤波器 g g g的卷积操作。
- ⊙ ⊙ ⊙表示元素积,根据这个公式,我们将 U T g U^Tg UTg整体当做一个可视化的卷积核 θ \theta θ,那么我们有:
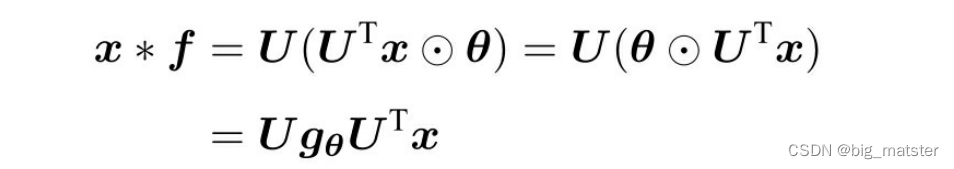
- 其中
g
θ
g_{\theta}
gθ是对角线元素为
θ
\theta
θ的对角阵。
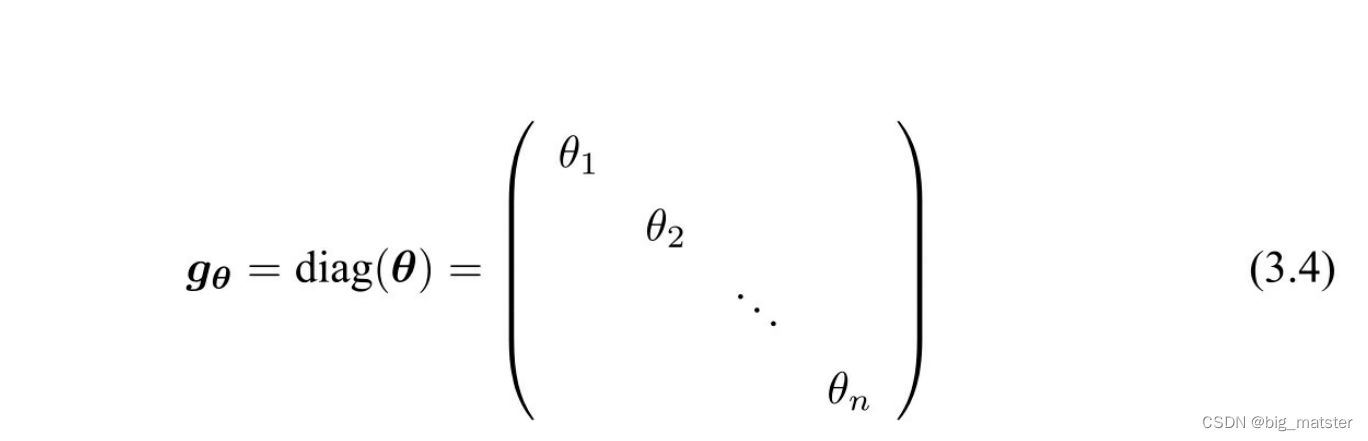



- 图卷积可以重构出网络上的卷积神经网络的。

谱域
指将信号转换为能量或功率的域,通过对能量或功率的分析来研究信号的能量或功率分布。常用的转换方法是使用功率谱密度函数。在谱域中,信号可以表示为各个频率分量的能量或功率。
空域
指将信号转换为空间坐标的域,通过对空间坐标的分析来研究信号的空间特性。在空域中,信号可以表示为在不同空间位置上的强度。
傅里叶变换
傅里叶变换公式如下:
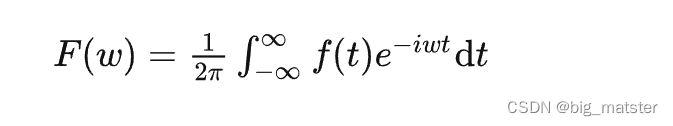
傅里叶变换就是将函数
f
(
t
)
f(t)
f(t)拆解成无数个不同频率正弦波之和的过程。
F
(
w
)
F(w)
F(w)表示角频率为
w
w
w的波的系数。
傅里叶变换也可以看作,函数
f
(
t
)
f(t)
f(t)向基函数
e
−
i
w
t
e^{-iwt}
e−iwt投影,
F
(
w
)
F(w)
F(w)表示
w
w
w对应基上的坐标。
图傅里叶变换
对图信号进行傅里叶变换:用拉普拉斯矩阵的特征向量作为图傅里叶投影的基。设拉普拉斯矩阵可进行如下特征分解

经验
慢慢的将图卷积给其吃透。会自己进行傅里叶变换。