PPT 截取必要信息。 课程网站做习题。总体 MOOC 过一遍

• 1、视频 + 学堂在线 习题
• 2、过 电子书，补充 【下载：本章 PDF 电子书 GitHub 界面链接】 [又看了一遍视频]
• 3、总体 MOOC 过一遍 习题

学堂在线 课程页面链接
中国大学MOOC 课程页面链接
B 站 视频链接

PPT和书籍下载网址： 【GitHub 链接】

---

强化学习的最终目标： 寻求最优策略

贝尔曼最优公式， 可以求解 最优状态值 和 最优策略。

————————
P1 如何 改进策略 ——> 选择 动作值 最大的动作

最优状态值、最优策略
the Bellman optimality equation (BOE) 贝尔曼最优公式

计算 状态值 $v_{\pi }(s)$， 然后计算 动作值 $q_{\pi }(s)$

选择 动作值 最大的动作可以得到 比较好的策略 。

选择 动作值 大的策略， 不断迭代， 一定可以得到 最优策略。

——————

P2 最优策略 定义

用 状态值 来评估一个策略的好坏：

若 对于 所有的 $s\in \mathcal{S}$， 均满足 $v_{{\pi }_1}(s)\ge v_{{\pi }_2}(s)$。 则认为 策略 1 比 策略 2 好。

最优策略 ${\pi }^{\ast }$： 对 所有 $s$ 和 所有策略 $\pi$， 均有 $v_{{\pi }^{\ast }}(s)\ge v_{\pi }(s)$。

与所有其他策略相比，最优策略在每个状态下都具有最大的状态值。

最优策略是否一定存在?
最优策略是唯一的吗?
最优策略是随机的还是确定的?
如何获得最优策略?

在后续内容中，需要 求解 形如 $f(v)=v$ 的方程，这正是 压缩映射定理【不动点定理】的相关内容。可证得 最优策略 对应的最优状态值 存在且唯一。

3.3 贝尔曼最优公式

$\begin{array}{rl}v(s)& =\underset{\pi }{\max }\sum _a\pi (a|s)(\sum _{r}p(r|s,a)r+\gamma \sum _{s^{\prime }}p(s^{\prime }|s,a)v(s^{\prime })),\forall s\in \mathcal{S}\\ & =\underset{\pi }{\max }\sum _a\pi (a|s)q(s,a),s\in \mathcal{S}\end{array}$

通过求解这个方程， 可以获得 最优策略 和 最优状态值。

• 已知：$p(r|s,a),p(s^{\prime }|s,a)$
• 未知：$v(s),v(s^{\prime })$

$\forall$$\forall$

贝尔曼最优方程的 矩阵-向量形式：

$\mathbf{v}=\underset{\pi }{\max }({\mathbf{r}}_{\pi }+\gamma {\mathbf{P}}_{\pi }\mathbf{v})$

• $[r_{\pi }{]}_s\triangleq \sum _a\pi (a|s)\sum _{r}p(r|s,a)r$
• $[P_{\pi }{]}_{s,s^{\prime }}=p(s^{\prime }|s)\triangleq \sum _a\pi (a|s)\sum _{s^{\prime }}p(s^{\prime }|s,a)$

$\triangleq$$\triangleq$

如何求解这个方程?
存在性：这个方程有解吗?
唯一性：这个方程的解是否唯一?
最优性：这个解与最优策略有什么关系?

一个式子， 两个未知量。如何求解 右侧的最大化？

类似地， 求解 贝尔曼最优方程

$v(s)=\underset{\pi }{\max }\sum _a\pi (a|s)q(s,a)$

受上述例子启发， 由于 $\sum _a\pi (a|s)=1$

$\sum _a\pi (a|s)q(s,a)\le \sum _a\pi (a|s)\underset{a}{\max }q(s,a)=\underset{a}{\max }q(s,a)$

$\sum _a\pi (a|s)q(s,a)$ 是类似于 上述例子中的求和式，根据经验，让取得最大的 $q(s,a)$ 【相当于 $q_3$】相应的概率 $\pi (a|s)$ 【相当于 $c_3$】为 1， 其它情况相应的 $\pi (a|s)$ 为 0， 此时能获得最大值

即 令 $\pi (a|s)=\{\begin{array}{rlr}& 1,& a=a^{\ast }\\ & 0,& a\ne a^{\ast }\end{array}$

• $a^{\ast }$：最大的 $q$ 值对应的 action。 $a^{\ast }=\arg \underset{a}{\max }q(s,a)$

最优策略 $\pi (s)$ 是选择具有 最大 $q(s,a)$ 的动作的策略。

——————

3.3.3 压缩映射定理 ： 求解 v = f(v)

P3

压缩映射定理 是分析一般非线性方程的有力工具。它也被称为不动点定理。

回到正题：

令 $f(\mathbf{v})=\underset{\pi }{\max }({\mathbf{r}}_{\pi }+\gamma {\mathbf{P}}_{\pi }\mathbf{v})$

$\mathbf{v}=f(\mathbf{v})$

映射后的距离 比 之前 小。

示例：

该定理描述了 不动点 和 压缩映射 之间的关系

只要是 具有 形如 $x=f(x)$ 的压缩映射， 必存在 一个 不动点 满足 $f(x^{\ast })=x^{\ast }$ ，且这个不动点是 唯一的。可通过 迭代式 $x_{k+1}=f(x_k)$ 求解。

压缩映射定理不仅可以判断非线性方程的解是否存在，而且还提供了求解该方程的数值算法。

P53-

• 证明 1： 压缩映射定理 P53- [见 后文补充]

如何利用 压缩映射定理 提出的 迭代算法 计算一些方程的不动点

例子：

3.3.4 贝尔曼最优公式的右侧 具有 压缩性

为了 应用 上述的 压缩映射定理 求解 贝尔曼最优方程 ， 需要 证明 $f(v)$ 是具有 收缩 的性质。

• 证明 2： 贝尔曼最优方程 的右侧 是 压缩映射的 P55- [ 见 后文补充]

3.4 贝尔曼最优方程 的解

上述 内容 证明了 贝尔曼最优方程 可以 运用 压缩映射定理 进行分析，可通过 迭代式 求解。

最优策略 ${\pi }^{\ast }=\arg \underset{\pi }{\max }(r_{\pi }+\gamma P_{\pi }{v}^{\ast })$

$v^{\ast }$ 是不动点， 因为 $v^{\ast }=f(v^{\ast })$。

贝尔曼最优公式 是 策略为最佳策略时的贝尔曼公式。

这个策略 是不是 最优的 ？
状态值 $v_{{\pi }^{\ast }}$ 是不是 最大的 ?

贝尔曼最优公式的不动点解 【最终的收敛值】 $v^{\ast }$ 就是 最大的状态值，此时的 ${\pi }^{\ast }$ 为最优策略。 [因为 对应的状态值最大]

BOE： 描述了 最优状态值 和 最优策略。

• 证明 3： 贝尔曼最优方程的解对应 最大状态值 和 最优策略 P58- [见 后文补充]

最优策略 ${\pi }^{\ast }$ 长 啥样呢？

总存在一个确定性的最优贪婪策略。

同样是类似于之前的求和式，令 $q^{\ast }(s,a)$ 最大的对应 $\pi (a|s)$ 为 1， 其它 为 0 。可获得 最大值。

正是证明了之前提到的 最优策略 $\pi (s)$ 是选择具有 最大 $q(s,a)$ 的动作的策略。

$v^{\ast }$ 的值是唯一的，但 $v^{\ast }$ 对应的最优策略可能不是唯一的。

————————

3.5 哪些因素影响最佳策略

P4 3.5

什么因素 决定最优策略 ？

最优策略的影响因素： 回报 $r$，折扣率 $\gamma$

$\gamma$小， 短视；即时奖励 [选择即时奖励最大的行动，而不是总回报最大的行动。]
$\gamma$大，目光长远； 延迟奖励

靠近目标的状态值较大，而远离目标的状态值较低。

• 如果一个状态必须沿着更长的轨迹到达目标，那么由于折扣率的存在，它的状态值就会变小。

$r$只关心 动作间的 奖励相对值。

$r~$ 友好的 波浪线强制空格

• 证明 4： 对所有 reward 统一进行 仿射变换， 最优策略 保持不变 P62- [见 后文补充]

当奖励都为 正 或 都为负的时候 可以 依据 以上定理 进行变换。最优策略 只和 奖励间的 相对值 有关

例子：

绕路

贝尔曼最优方程的 解对应 最佳状态值 和 最优策略。

小结：

3.7 节

什么是最优策略?
如果一个策略对应的状态值大于或等于任何其他策略，则该策略是最优的。
应该注意的是，这个特定的最优性定义仅对表格强化学习算法有效。当值或策略由函数近似时，必须使用不同的度量来定义最优策略。

最优政策是随机的还是确定的 ?
最优策略可以是确定性的，也可以是随机的。一个很好的事实是，总是存在确定性贪婪最优策略。

如果我们希望最优策略在到达目标之前避免无意义的弯路，我们是否应该在每一步都增加一个负奖励，以使 agent 尽快到达目标?
首先，在每一步中引入一个额外的负奖励是奖励的仿射变换，它不会改变最优策略。其次，折扣率可以自动鼓励 agent 尽快达到目标。这是因为无意义的弯路会增加轨迹长度，减少 discounted return。

-——————
习题 笔记：

最优策略不一定唯一。

补充

证明 1： 压缩映射定理

压缩映射定理 不仅可以判断非线性方程的解是否存在，而且还提供了求解该方程的数值算法。 $x_{k+1}=f(x_k)$。不断迭代即可获得 解。

P8 Box 3.1

补充：

根据 柯西极限存在准则，证明 不动点 存在。

1、证明 当 { x k } k = 1 ∞ \{x_k\}_{k=1}^\infty {xk​}k=1∞​ 时，$x_k=f(x_{k-1})$ 收敛。

这个证明依赖于柯西序列。一个序列 $x_1,x_2,\cdots \in \mathbb{R}$， 如果对于任何小的 $\epsilon >0$，存在 $N$， 对于所有 $m,n>N$， 使得 $||x_m-x_n||<\epsilon$。

直观的解释是存在一个有限整数 $N$， 使得 $N$ 之后的所有元素彼此足够接近。

柯西序列之所以重要，是因为它保证了柯西序列收敛于某个有限值。
它的收敛性将用于证明 压缩映射定理。

注意，对于所有的 $m,n>N$，我们必须有 $||x_m-x_n||<\epsilon$。
如果我们仅仅有 $x_{n+1}-x_n\to 0$，就不足以断言这个序列是柯西序列。
例如，对于 $x_n=\sqrt{n}$，$x_{n+1}-x_n\to 0$ 成立，但显然，$x_n=\sqrt{n}$ 是发散的。

证明 { x k = f ( x k − 1 ) } k = 1 ∞ \{x_k=f(x_{k-1})\}_{k=1}^\infty {xk​=f(xk−1​)}k=1∞​ 是柯西序列， 因此是 收敛的。

——————————————

由于 $f$ 是 收缩映射， 则有

$||x_{k+1}-x_k||=||f(x_k)-f(x_{k-1})||\le \gamma ||x_k-x_{k-1}||$

类似地 ，有
$||x_k-x_{k-1}||\le \gamma ||x_{k-1}-x_{k-2}||$
$⋮$
$||x_2-x_1||\le \gamma ||x_1-x_0||$

则

$\begin{array}{rl}||x_{k+1}-x_k||& \le \gamma ||x_k-x_{k-1}||\\ & \le {\gamma }^2||x_{k-1}-x_{k-2}||\\ & ⋮\\ & \le {\gamma }^k||x_1-x_0||\end{array}$

由于 $\gamma <1$, 对 任意 $x_1,x_0$ ，当 $k\to \infty$， $||x_{k+1}-x_k||$ 以指数速度 收敛到 0。

正如 前文所述， 仅满足 $x_{n+1}-x_n\to 0$ ， 无法得到 收敛的结论。 如 发散 的 $x_n=\sqrt{n}$ 。

需要进一步考虑 $m>n$ 时，

$\begin{array}{rl}||x_m-x_n||& =||x_m-x_{m-1}+x_{m-1}-\cdots -x_{n+1}+x_{n+1}-x_n||\\ & \le ||x_m-x_{m-1}||+\cdots +||x_{n+1}-x_n||\\ & \le {\gamma }^{m-1}||x_1-x_0||+\cdots +{\gamma }^n||x_1-x_0||\\ & ={\gamma }^n({\gamma }^{m-1-n}+\cdots +1)||x_1-x_0||\\ & \le {\gamma }^n\cdot \sum _{i=1}^{\infty }{\gamma }^i\cdot ||x_1-x_0||\gamma 的幂次项扩展到无穷多项\\ & =\frac{{\gamma }^n}{1-\gamma }||x_1-x_0||\end{array}$

对于右侧， $\gamma <1$，为某个 小的值

对任意小的 $\epsilon$， 总能找到 $N$， 使得当 $m,n>N$ ，有 $||x_m-x_n||<\epsilon$，满足柯西极限存在准则， 数列 { x k } \{x_k\} {xk​} 收敛。

假设收敛到 $x^{\ast }$， $\underset{k\to \infty }{\lim }{x}_k=x^{\ast }$。

2、证明 $x^{\ast }=\underset{k\to \infty }{\lim }{x}_k$ 是一个不动点。

由于 $||f(x_k)-x_k||=||x_{k+1}-x_k||\le {\gamma }^k||x_1-x_0||$

已知 $||f(x_k)-x_k||$ 以指数速度 收敛于 0。则 $f(x^{\ast })=x^{\ast }$ 两边同时 取极限

$\underset{k\to \infty }{\lim }||f(x_k)-x_k||=0$

3、证明 不动点 唯一。

假设 存在另外的不动点 $x^{\prime }$， 满足 $f(x^{\prime })=x^{\prime }$

$||x^{\prime }-x^{\ast }||=||f(x^{\prime })-f(x^{\ast })||\le \gamma ||x^{\prime }-x^{\ast }||$

由于 $\gamma <1$, 当且仅当 $||x^{\prime }-x^{\ast }||=0$ 时不等式成立。因此， 只能是 $x^{\prime }=x^{\ast }$。

或者不等式两边同除 $||x^{\prime }-x^{\ast }||$， 得到 $\gamma \ge 1$，与题设 $\gamma <1$矛盾，因此不动点唯一。

4、证明 $x_k$ 以指数速度收敛于 $x^{\ast }$。

由之前的 $||x_m-x_n||\le \frac{{\gamma }^n}{1-\gamma }||x_1-x_0||$

由于 $m$ 可以是任意大。

$x^{\ast }-x_n=\underset{m\to \infty }{\lim }||x_m-x_n||\le \frac{{\gamma }^n}{1-\gamma }||x_1-x_0||$

由于 $\gamma <1$， 当 $n\to \infty$ 时，误差以指数速度 收敛于 0。

——————————
补充： 参考链接

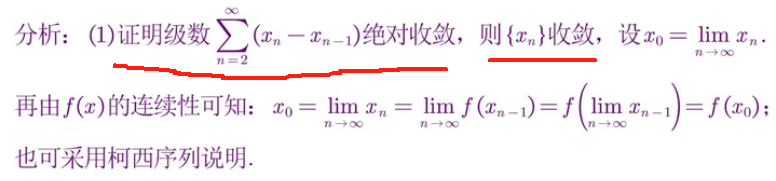
其它可参考链接：

链接 1：数分之梯丨压缩映射定理——同济大学陈滨
链接 2：柯西收敛准则有啥用？当然是证明压缩映射原理！

证明 2：证明 贝尔曼最优方程 的右侧 是 压缩映射的

考虑 两个 向量 ${\mathbf{v}}_1,{\mathbf{v}}_2\in {\mathbb{R}}^{|\mathcal{S}|}$

${\pi }_1^{\ast }\dot{=}\arg \underset{\pi }{\max }({\mathbf{r}}_{\pi }+\gamma {\mathbf{P}}_{\pi }{\mathbf{v}}_1)$

${\pi }_2^{\ast }\dot{=}\arg \underset{\pi }{\max }({\mathbf{r}}_{\pi }+\gamma {\mathbf{P}}_{\pi }{\mathbf{v}}_2)$

$f({\mathbf{v}}_1)=\underset{\pi }{\max }({\mathbf{r}}_{\pi }+\gamma {\mathbf{P}}_{\pi }{\mathbf{v}}_1)={\mathbf{r}}_{{\pi }_1^{\ast }}+\gamma {\mathbf{P}}_{{\pi }_1^{\ast }}{\mathbf{v}}_1\ge {\mathbf{r}}_{{\pi }_2^{\ast }}+\gamma {\mathbf{P}}_{{\pi }_2^{\ast }}{\mathbf{v}}_1$ 对于同一状态值 $v_1$ ，最佳策略 ${\pi }_1^{\ast }$ 相应的状态值 必然大于 其它策略的

$f({\mathbf{v}}_2)=\underset{\pi }{\max }({\mathbf{r}}_{\pi }+\gamma {\mathbf{P}}_{\pi }{\mathbf{v}}_2)={\mathbf{r}}_{{\pi }_2^{\ast }}+\gamma {\mathbf{P}}_{{\pi }_2^{\ast }}{\mathbf{v}}_2\ge {\mathbf{r}}_{{\pi }_1^{\ast }}+\gamma {\mathbf{P}}_{{\pi }_1^{\ast }}{\mathbf{v}}_2$

$\ge$ 是 元素级的。

$\begin{array}{rl}f({\mathbf{v}}_1)-f({\mathbf{v}}_2)& ={\mathbf{r}}_{{\pi }_1^{\ast }}+\gamma {\mathbf{P}}_{{\pi }_1^{\ast }}{\mathbf{v}}_1-({\mathbf{r}}_{{\pi }_2^{\ast }}+\gamma {\mathbf{P}}_{{\pi }_2^{\ast }}{\mathbf{v}}_2)\\ & \le {\mathbf{r}}_{{\pi }_1^{\ast }}+\gamma {\mathbf{P}}_{{\pi }_1^{\ast }}{\mathbf{v}}_1-({\mathbf{r}}_{{\pi }_1^{\ast }}+\gamma {\mathbf{P}}_{{\pi }_1^{\ast }}{\mathbf{v}}_2)\\ & =\gamma {\mathbf{P}}_{{\pi }_1^{\ast }}({\mathbf{v}}_1-{\mathbf{v}}_2)\end{array}$

$\begin{array}{rl}f({\mathbf{v}}_2)-f({\mathbf{v}}_1)& ={\mathbf{r}}_{{\pi }_2^{\ast }}+\gamma {\mathbf{P}}_{{\pi }_2^{\ast }}{\mathbf{v}}_2-({\mathbf{r}}_{{\pi }_1^{\ast }}+\gamma {\mathbf{P}}_{{\pi }_1^{\ast }}{\mathbf{v}}_1)\\ & \le {\mathbf{r}}_{{\pi }_2^{\ast }}+\gamma {\mathbf{P}}_{{\pi }_2^{\ast }}{\mathbf{v}}_2-({\mathbf{r}}_{{\pi }_2^{\ast }}+\gamma {\mathbf{P}}_{{\pi }_2^{\ast }}{\mathbf{v}}_1)\\ & =\gamma {\mathbf{P}}_{{\pi }_2^{\ast }}({\mathbf{v}}_2-{\mathbf{v}}_1)\end{array}$

$\gamma {\mathbf{P}}_{{\pi }_2^{\ast }}({\mathbf{v}}_1-{\mathbf{v}}_2)\le f({\mathbf{v}}_1)-f({\mathbf{v}}_2)\le \gamma {\mathbf{P}}_{{\pi }_1^{\ast }}({\mathbf{v}}_1-{\mathbf{v}}_2)$

令 z = ˙ max ⁡   { ∣ γ P π 2 ∗ ( v 1 − v 2 ) ∣ , ∣ γ P π 1 ∗ ( v 1 − v 2 ) ∣ } ∈ R ∣ S ∣ z\dot=\max~\{|\gamma\bm P_{\pi_2^*}(\bm v_1-\bm v_2)|, |\gamma\bm P_{\pi_1^*}(\bm v_1-\bm v_2)|\}\in\mathbb R^{|\cal S|} z=˙max {∣γPπ2∗​​(v1​−v2​)∣,∣γPπ1∗​​(v1​−v2​)∣}∈R∣S∣

$z\ge 0$

$-z\le \gamma {\mathbf{P}}_{{\pi }_2^{\ast }}({\mathbf{v}}_1-{\mathbf{v}}_2)\le f({\mathbf{v}}_1)-f({\mathbf{v}}_2)\le \gamma {\mathbf{P}}_{{\pi }_1^{\ast }}({\mathbf{v}}_1-{\mathbf{v}}_2)\le z$

$|f({\mathbf{v}}_1)-f({\mathbf{v}}_2)|\le z$

最大模 $||f({\mathbf{v}}_1)-f({\mathbf{v}}_2)|{|}_{\infty }\le ||z|{|}_{\infty }$

$p_i^T$， $q_i^T$ 分别为 ${\mathbf{P}}_{{\pi }_1^{\ast }}$ 和 ${\mathbf{P}}_{{\pi }_2^{\ast }}$ 的 第 $i$ 行。

z i = max ⁡   { γ ∣ p i T ( v 1 − v 2 ) ∣ , γ ∣ q i T ( v 1 − v 2 ) ∣ } z_i=\max~\{\gamma |p_i^T(\bm v_1-\bm v_2)|, \gamma|q_i^T(\bm v_1-\bm v_2)|\} zi​=max {γ∣piT​(v1​−v2​)∣,γ∣qiT​(v1​−v2​)∣}

$p_i$ 是一个包含所有非负元素的向量并且所有元素的和等于 1。

$|p_i^T({\mathbf{v}}_1-{\mathbf{v}}_2)|\le p_i^T|{\mathbf{v}}_1-{\mathbf{v}}_2|\le ||{\mathbf{v}}_1-{\mathbf{v}}_2|{|}_{\infty }$

类似地 ， $|q_i^T({\mathbf{v}}_1-{\mathbf{v}}_2)|\le ||{\mathbf{v}}_1-{\mathbf{v}}_2|{|}_{\infty }$

$z_i\le \gamma ||{\mathbf{v}}_1-{\mathbf{v}}_2|{|}_{\infty }$

$||z|{|}_{\infty }=\underset{i}{\max }|z_i|\le \gamma ||{\mathbf{v}}_1-{\mathbf{v}}_2|{|}_{\infty }$

即 $||f({\mathbf{v}}_1)-f({\mathbf{v}}_2)|{|}_{\infty }\le \gamma ||{\mathbf{v}}_1-{\mathbf{v}}_2|{|}_{\infty }$

证毕。

证明 3： 贝尔曼最优方程的解对应 最大状态值 和 最优策略

P58

对于 任意 策略 $\pi$, 满足 贝尔曼方程为 $v_{\pi }=r_{\pi }+\gamma P_{\pi }{v}_{\pi }$

由于 最优策略 $v^{\ast }=\underset{\pi }{\max }(r_{\pi }+\gamma P_{\pi }{v}^{\ast })=r_{{\pi }^{\ast }}+\gamma P_{{\pi }^{\ast }}{v}^{\ast }\ge r_{\pi }+\gamma P_{\pi }{v}^{\ast }$

$v^{\ast }-v_{\pi }\ge r_{{\pi }^{\ast }}+\gamma P_{{\pi }^{\ast }}{v}^{\ast }-(r_{\pi }+\gamma P_{\pi }{v}_{\pi })=\gamma P_{\pi }(v^{\ast }-v_{\pi })$

重复应用上述不等式：

$v^{\ast }-v_{\pi }\ge \gamma P_{\pi }(v^{\ast }-v_{\pi })\ge {\gamma }^2{P}_{\pi }^2(v^{\ast }-v_{\pi })\ge \cdots \ge {\gamma }^n{P}_{\pi }^n(v^{\ast }-v_{\pi })$

$v^{\ast }-v_{\pi }\le \underset{n\to \infty }{\lim }{\gamma }^n{P}_{\pi }^n(v^{\ast }-v_{\pi })=0$

由于 $\gamma <1$ 且 $P_{\pi }^n$ 是 元素均小于或等于 1 的非负矩阵 $P_{\pi }^{n}1=1$

因此 $v^{\ast }\ge v_{\pi }$ 对于任意 $\pi$ 均成立。

证明 4： 对所有 reward 统一进行 仿射变换， 最优策略 不变

最优策略不变性

最优策略 ${\mathbf{v}}^{\ast }=\underset{\pi }{\max }({\mathbf{r}}_{\pi }+\gamma {\mathbf{P}}_{\pi }{\mathbf{v}}^{\ast })$

对 其中的 每个奖励值 $r$ 都进行 仿射变换 $\alpha r+\beta$

则相应的 最优 状态值 ${\mathbf{v}}^{\prime }=\alpha {\mathbf{v}}^{\ast }+\frac{\beta }{1-\gamma }\left[\begin{array}{c}1\\ 1\\ ...\\ 1\\ 1\end{array}\right]$

其中 折扣率 $\gamma \in (0,1)$
由 ${\mathbf{v}}^{\prime }$ 得到的最优策略 对于奖励值的仿射变换是不变的。

————————————————————————

P62 -

证明：

对 任意 策略 $\pi$， 令 $r_{\pi }=[\cdots ,r_{\pi }(s),\cdots {]}^T$

$r_{\pi }(s)=\sum _{a\in \mathcal{A}}\pi (a|s)\sum _{r\in \mathcal{R}}p(r|s,a)r,s\in \mathcal{S}$

如果 $r\to \alpha r+\beta$， 则 $r_{\pi }(s)\to \alpha r_{\pi }(s)+\beta$

$r_{\pi }\to \alpha r_{\pi }+\beta 1$， 其中 $1=[1,\cdots ,1{]}^T$

此时， 贝尔曼最优公式 变成：

${\mathbf{v}}^{\prime }=\underset{\pi }{\max }(\alpha {\mathbf{r}}_{\pi }+\beta 1+\gamma {\mathbf{P}}_{\pi }{\mathbf{v}}^{\prime })(3.9)$

设 ${\mathbf{v}}^{\prime }=\alpha {\mathbf{v}}^{\ast }+c1$ 是 上述 式 (3.9) 的解

将 ${\mathbf{v}}^{\prime }=\alpha {\mathbf{v}}^{\ast }+c1$ 代入 (3.9)

$\alpha {\mathbf{v}}^{\ast }+c1=\underset{\pi }{\max }(\alpha {\mathbf{r}}_{\pi }+\beta 1+\gamma {\mathbf{P}}_{\pi }(\alpha {\mathbf{v}}^{\ast }+c1))=\underset{\pi }{\max }(\alpha {\mathbf{r}}_{\pi }+\beta 1+\gamma \alpha {\mathbf{P}}_{\pi }{\mathbf{v}}^{\ast }+\gamma c1)$

注意 ${\mathbf{P}}_{\pi }1=1$

$\alpha {\mathbf{v}}^{\ast }=\underset{\alpha {\mathbf{v}}^{\ast }}{\underbrace{\underset{\pi }{\max }(\alpha {\mathbf{r}}_{\pi }+\gamma \alpha {\mathbf{P}}_{\pi }{\mathbf{v}}^{\ast })}}+\beta 1++\gamma c1-c1$

即 $\beta 1++\gamma c1-c1=0$

$c=\frac{\beta }{1-\gamma }$

说明 ${\mathbf{v}}^{\prime }=\alpha {\mathbf{v}}^{\ast }+c1$ 是 式 (3.9) 的解，其中 $c=\frac{\beta }{1-\gamma }$。

又因为 式 (3.9) 也是 贝尔曼最优公式， $v^{\prime }$ 就是唯一解。

由于 $v^{\prime }$ 是 $v^{\ast }$ 的 仿射变换，状态值 之间的 相对关系 保持不变。
因此， 根据 $v^{\prime }$ 得到的贪心最优策略 和 $v^{\ast }$ 的一样。