归并排序
归并排序(merge sort)是利用“归并”操作的一种排序方法。从有序表的讨论中得知,将两个有序表“归并”为一个有序表,无论是顺序表还是链表,归并操作都可以在线性时间复杂度内实现。归并排序的基本操作是将两个位置相邻的有序记录子序列R[i…m]R[m+1…n]归并为一个有序记录序列 R[i…n],如下图算法所示:

实现归并排序的基本思想是: 在待排序的原始记录序列 R[s…t]中取一个中间位置(s+t)/2,先分别对子序列 R[s…(s+t)/2]和 R[(s+t)/2+1…t]进行归并排序,然后调用上述算法便可实现整个序列 R[s…t]成为记录的有序序列。因此,归并排序的算法也可以是一个递归调用的算法,算法如下所示:


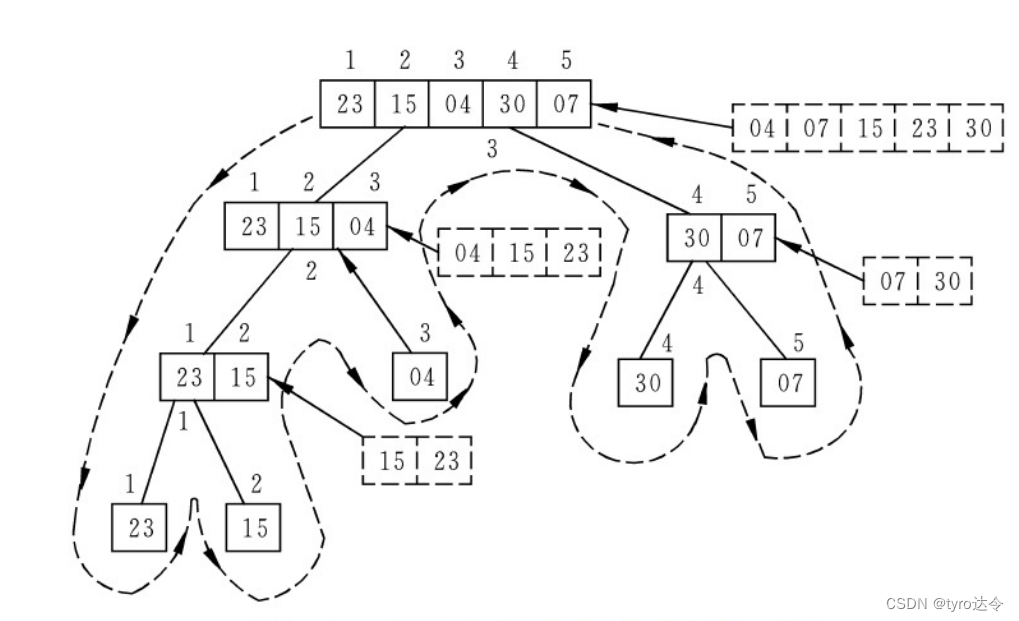
利用算法 3.11 对关键字序列 (23,15,04,30,07) 进行归并排序的过程如下图所示归并排序的时间复杂度为O(nlogn),空间复杂度为 O(n)。
归并排序是稳定的排序方法。
堆排序
堆排序(heap sort)是对选择排序的一种改进方法。在此首先需引进“堆”的概念。
堆的定义:堆是满足下列性质的数列(r1,r2,···,rn};

若上述数列是堆,则r1必是数列中的最小值或最大值,则分别称上述满足式所示关系的序列为小顶堆或大顶堆。
堆排序即是利用堆的特性对记录序列进行排序的一种排序方法。具体作法是:先按记录的关键字建一个“大顶堆”,因此选得一个关键字为最大的记录,然后与序列中最后一个记录交换,之后继续对序列中前 n-1 记录进行“筛选”,重新将它调整为一个“大顶堆”,再将堆顶记录和第 n-1 个记录交换。这样,有序性逐渐从右部向左扩大,如此反复直至排序结束。下图所示为堆排序的一个例子。
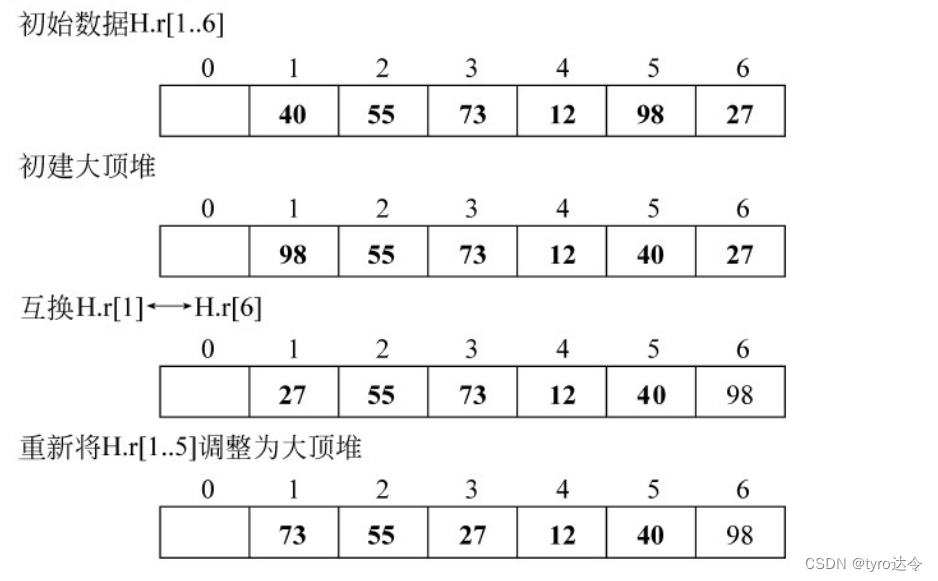

进一步讨论堆排序的算法需要有关完全二叉树的知识,堆排序的时间复杂度为 O(nlogn),空间复杂度为 O(1)。