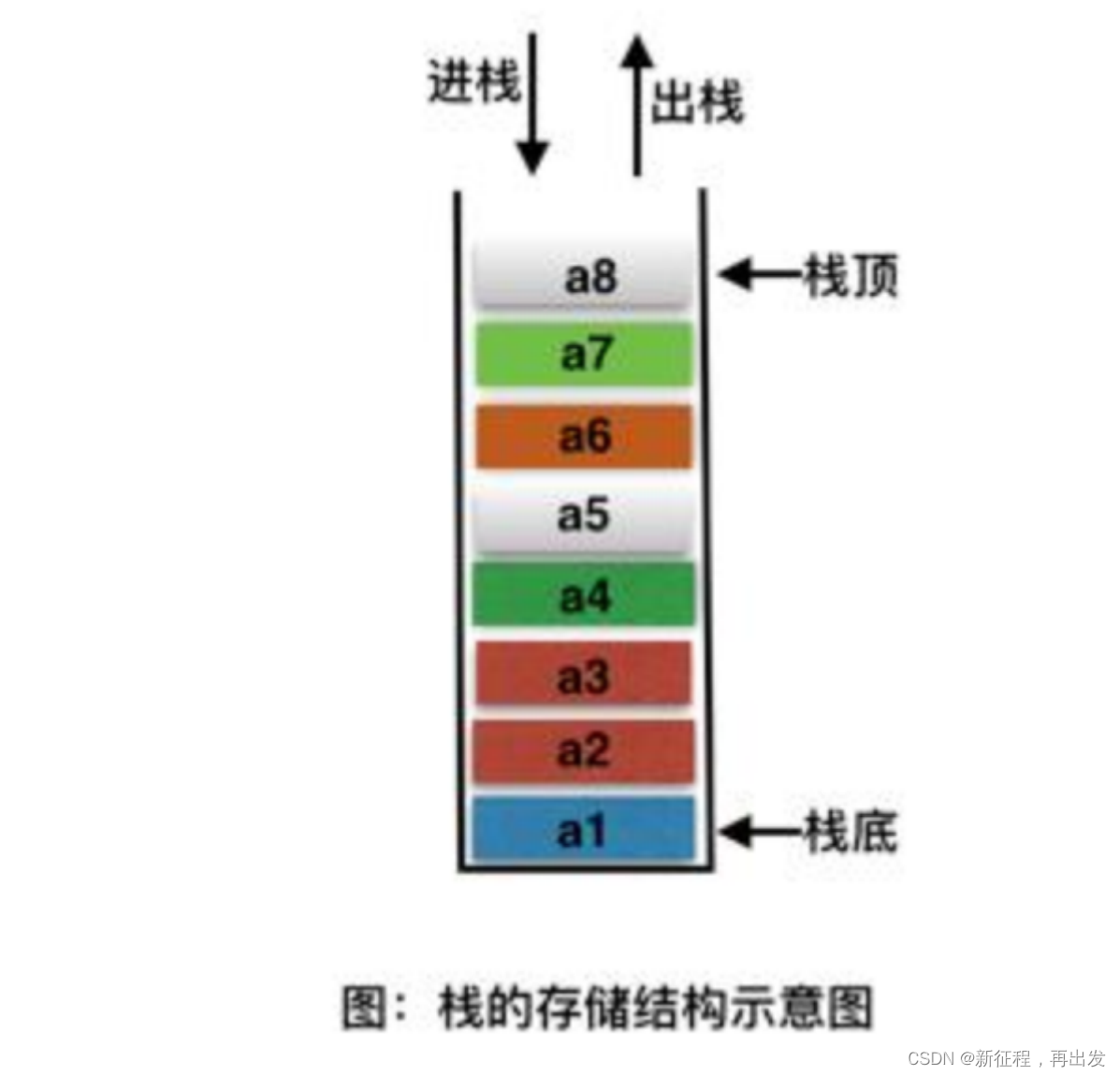
栈(stack)
栈( stack)是限制插入和删除只能在一个位置上进行的表,该位置是表的末端,叫做栈顶(top)。它是后进先出(LIFO)的。对栈的基本操作只有 push(进栈)和 pop(出栈)两种,前者相当于插入,后者相当于删除最后的元素。
队列(queue)
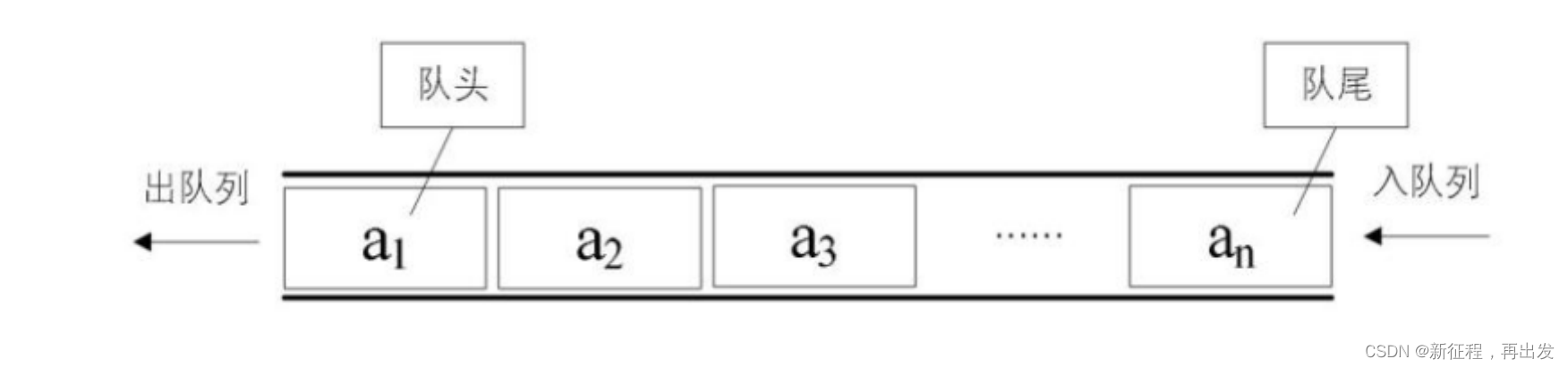
队列是一种特殊的线性表,特殊之处在于它只允许在表的前端(front)进行删除操作,而在表的后端(rear)进行插入操作,和栈一样,队列是一种操作受限制的线性表。进行插入操作的端称为队尾,进行删除操作的端称为队头。
链表(Link)
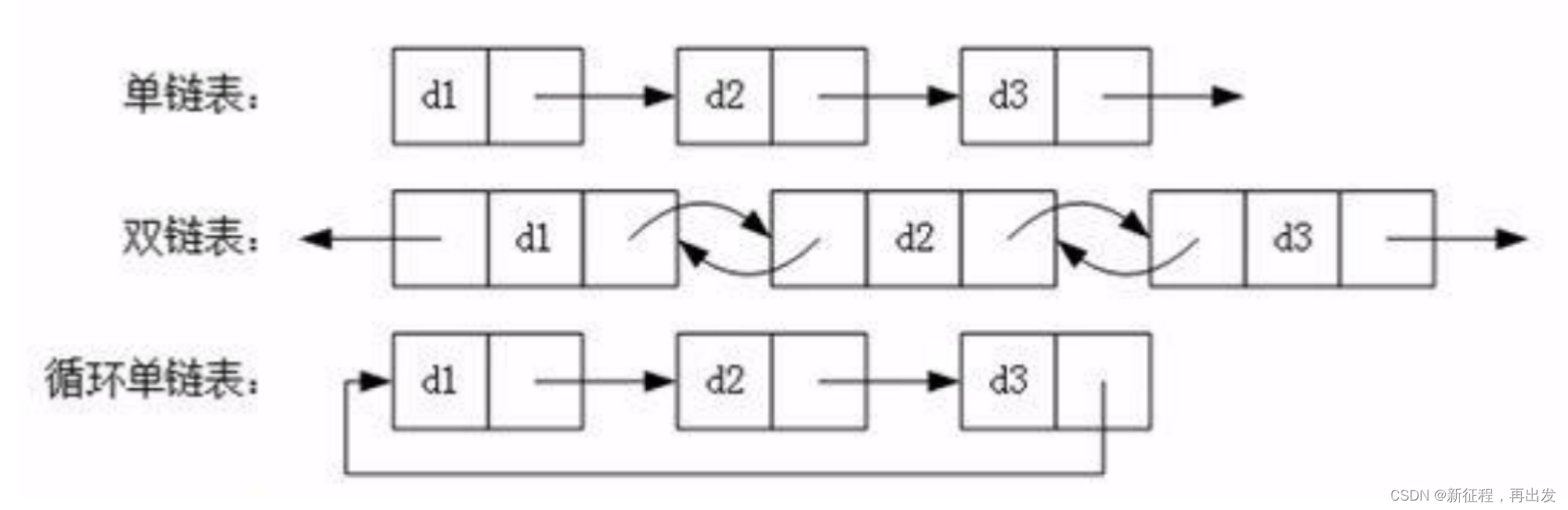
链表是一种数据结构,和数组同级。比如, Java 中我们使用的 ArrayList,其实现原理是数组。而LinkedList 的实现原理就是链表了。链表在进行循环遍历时效率不高,但是插入和删除时优势明显。
散列表(Hash Table)
散列表(Hash table,也叫哈希表)是一种查找算法,与链表、树等算法不同的是,散列表算法在查找时不需要进行一系列和关键字(关键字是数据元素中某个数据项的值,用以标识一个数据元素)的比较操作。
散列表算法希望能尽量做到不经过任何比较,通过一次存取就能得到所查找的数据元素,因而必须要在数据元素的存储位置和它的关键字(可用 key 表示)之间建立一个确定的对应关系,使每个关键字和散列表中一个唯一的存储位置相对应。因此在查找时,只要根据这个对应关系找到给定关键字在散列表中的位置即可。这种对应关系被称为散列函数(可用 h(key)表示)。
用的构造散列函数的方法有:
- 直接定址法: 取关键字或关键字的某个线性函数值为散列地址。即: h(key) = key 或 h(key) = a * key + b, 其中 a 和 b 为常数。
- 数字分析法
- 平方取值法: 取关键字平方后的中间几位为散列地址。
- 折叠法: 将关键字分割成位数相同的几部分,然后取这几部分的叠加和作为散列地址。
- 除留余数法: 取关键字被某个不大于散列表表长 m 的数 p 除后所得的余数为散列地址,即: h(key) = key MOD p p ≤ m
- 随机数法: 选择一个随机函数,取关键字的随机函数值为它的散列地址,即: h(key) = random(key)。
排序二叉树
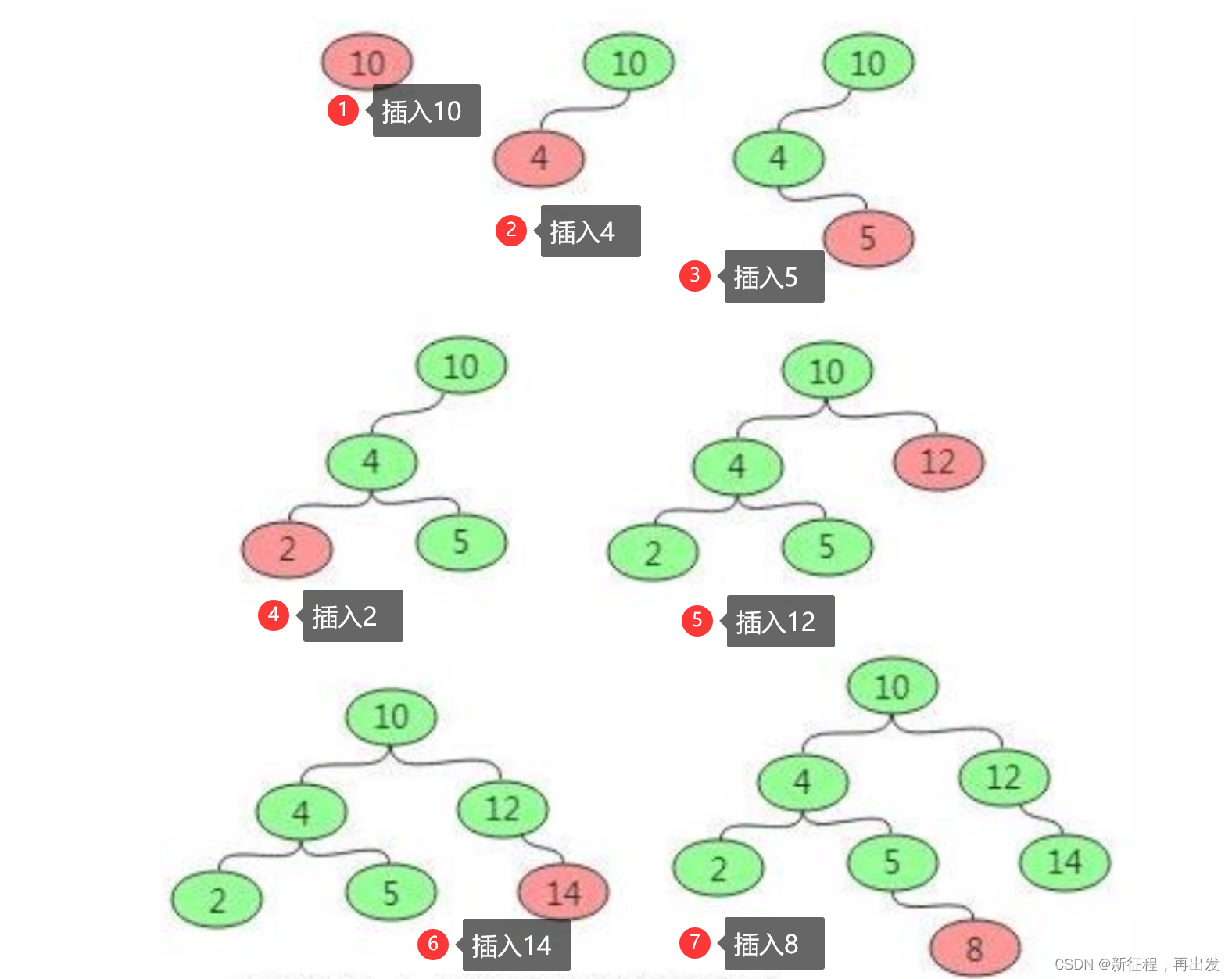
首先如果普通二叉树每个节点满足:左子树所有节点值小于它的根节点值,且右子树所有节点值大于它的根节点值,则这样的二叉树就是排序二叉树。
插入操作
首先要从根节点开始往下找到自己要插入的位置(即新节点的父节点);具体流程是:新节点与当前节点比较,如果相同则表示已经存在且不能再重复插入;如果小于当前节点,则到左子树中寻找,如果左子树为空则当前节点为要找的父节点,新节点插入到当前节点的左子树即可;如果大于当前节点,则到右子树中寻找,如果右子树为空则当前节点为要找的父节点,新节点插入到当前节点的右子树即可。
删除操作
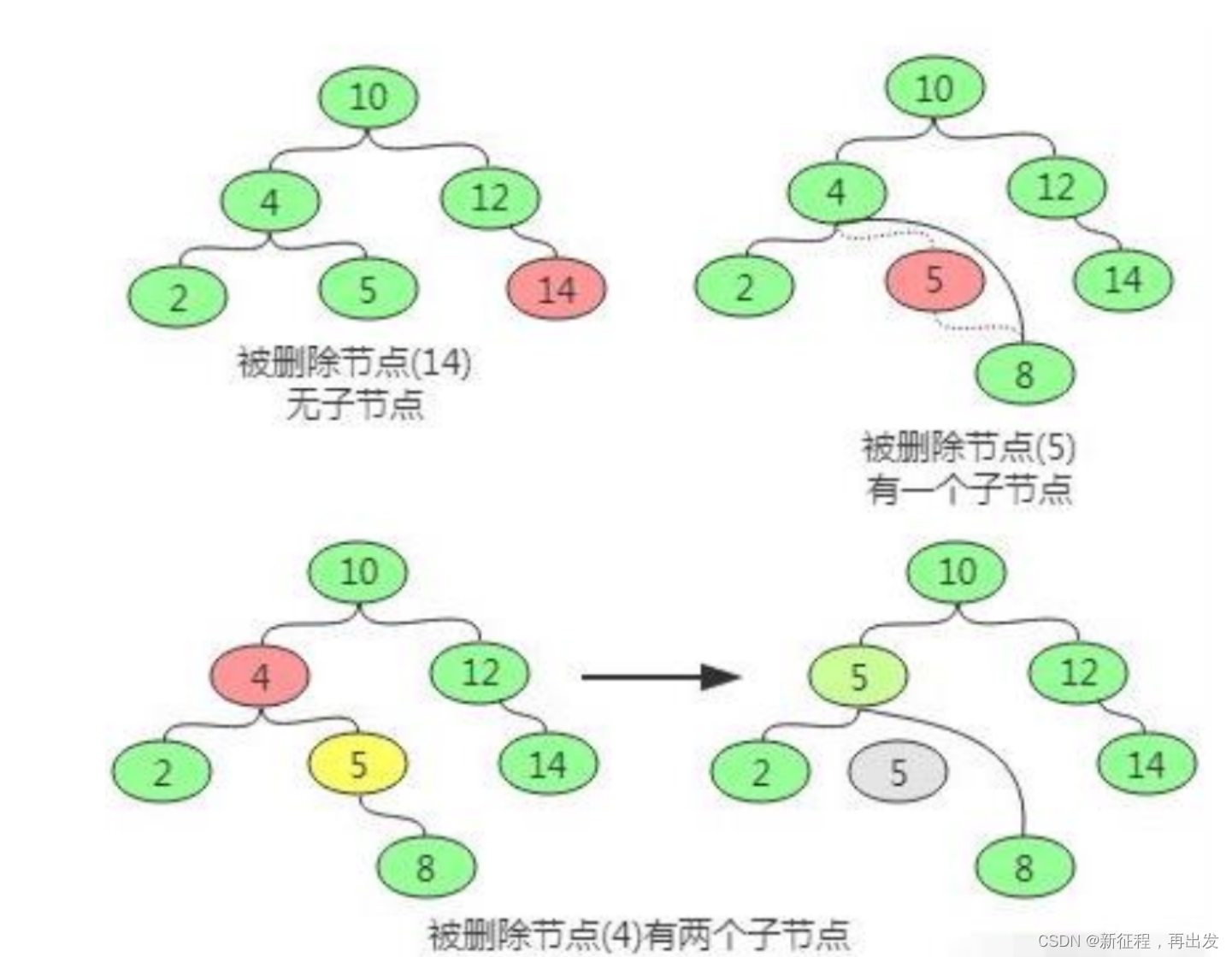
删除操作主要分为三种情况, 即要删除的节点无子节点,要删除的节点只有一个子节点,要删除的节点有两个子节点。
- 对于要删除的节点无子节点可以直接删除,即让其父节点将该子节点置空即可。
- 对于要删除的节点只有一个子节点,则替换要删除的节点为其子节点。
- 对于要删除的节点有两个子节点, 则首先找该节点的替换节点(即右子树中最小的节点),接着替换要删除的节点为替换节点,然后删除替换节点。
查询操作
查找操作的主要流程为:
先和根节点比较,如果相同就返回, 如果小于根节点则到左子树中归查找,如果大于根节点则到右子树中递归查找。
因此在排序二叉树中可以很容易获取最大(最右最深子节点)和最小(最左最深子节点)值。
前缀树
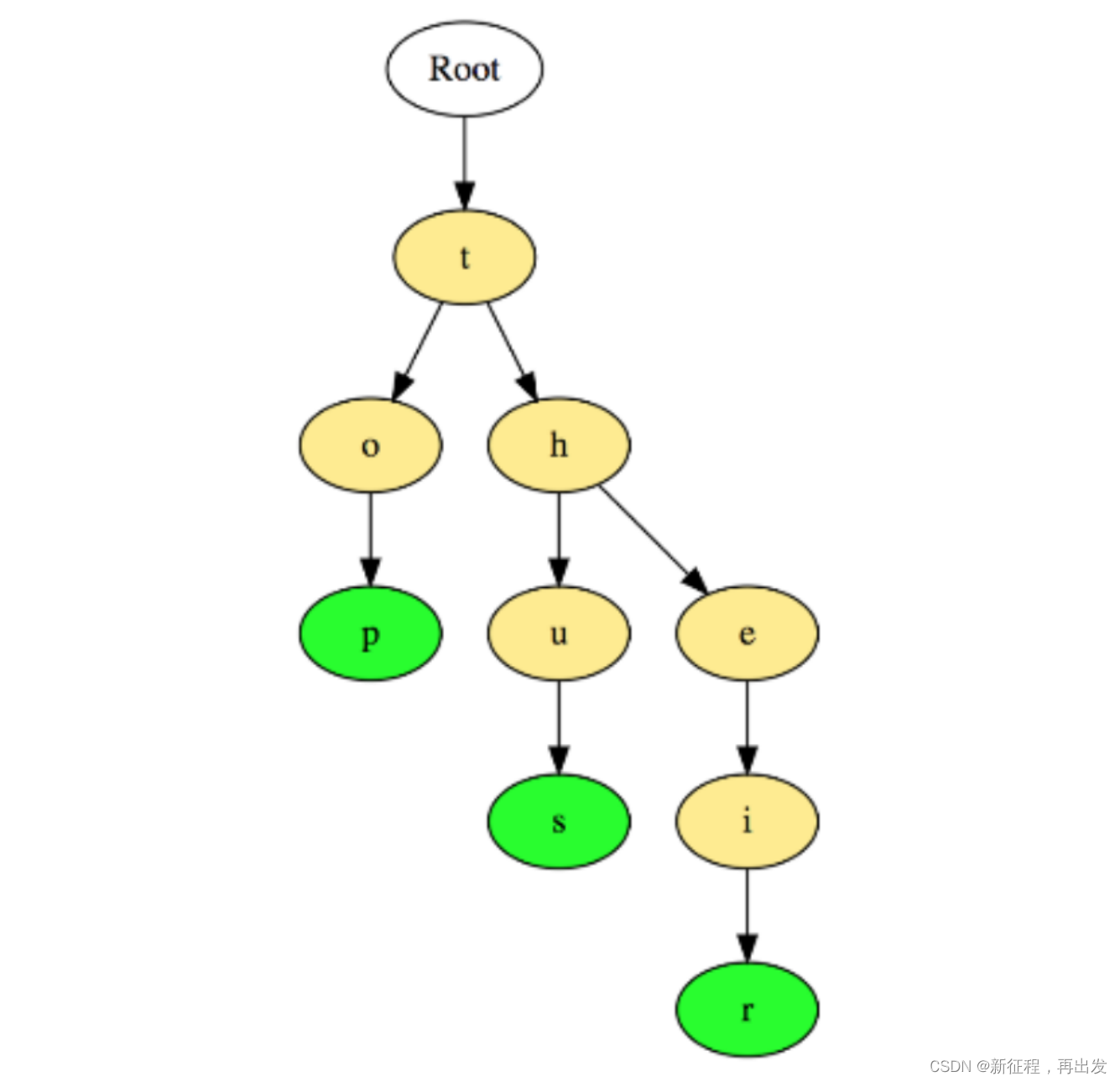
前缀树(Prefix Trees 或者 Trie)与树类似,用于处理字符串相关的问题时非常高效。它可以实现快速检索,常用于字典中的单词查询,搜索引擎的自动补全甚至 IP 路由。
下图展示了“top”, “thus”和“their”三个单词在前缀树中如何存储的:
红黑树
红黑树的特性
- 一个节点不是红色的就是黑色的。
- 根节点是黑色。
- 如果一个节点为红色,那么它的子节点一定为黑色。
- 叶子节点为黑色。
- 一个节点到它的子孙节点的所有路径包含相同数量的黑色节点。
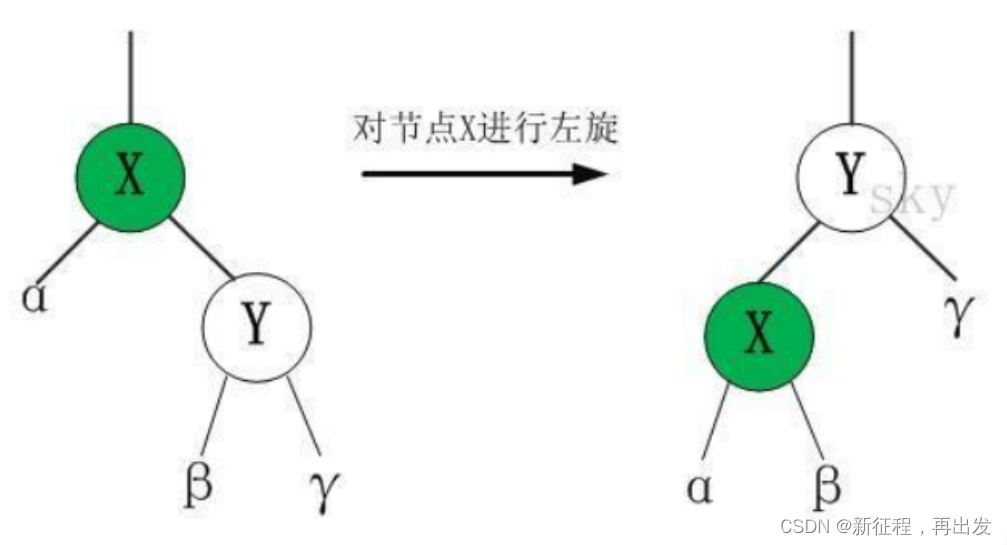
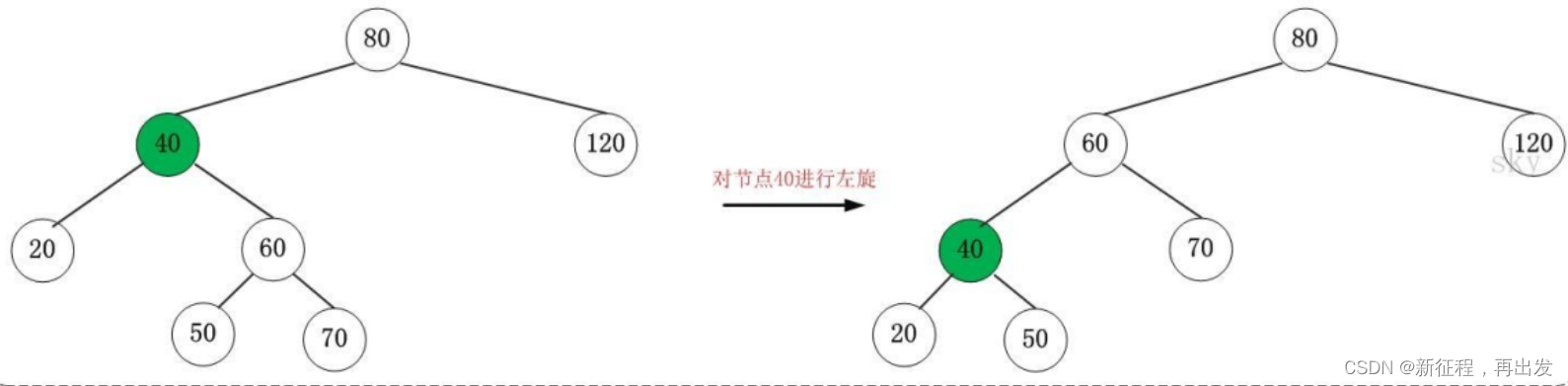
左旋
对 x 进行左旋,意味着,将“x 的右孩子”设为“x 的父亲节点”;即,将 x 变成了一个左节点(x成了为 z 的左孩子)!。 因此,左旋中的“左”,意味着“被旋转的节点将变成一个左节点”。
例子:
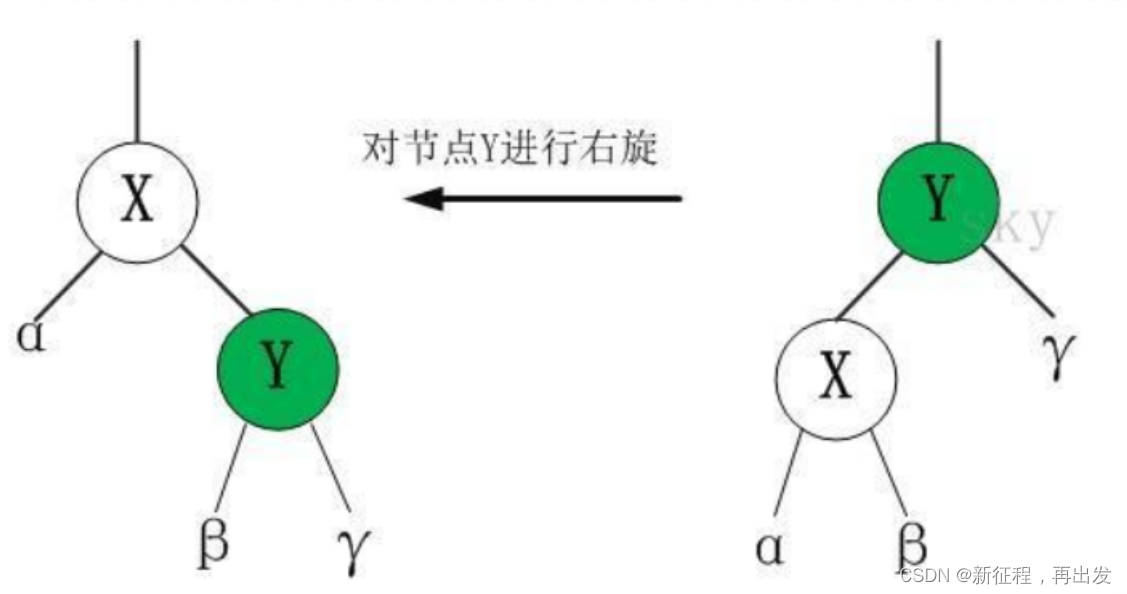
右旋
对 x 进行右旋,意味着,将“x 的左孩子”设为“x 的父亲节点”;即,将 x 变成了一个右节点(x成了为 y 的右孩子)! 因此,右旋中的“右”,意味着“被旋转的节点将变成一个右节点”。
添加
- 第一步: 将红黑树当作一颗二叉查找树,将节点插入。
- 第二步:将插入的节点着色为"红色"。
根据被插入节点的父节点的情况,可以将"当节点 z 被着色为红色节点,并插入二叉树"划分为三种情况来处理。- ① 情况说明:被插入的节点是根节点。
处理方法:直接把此节点涂为黑色。 - ② 情况说明:被插入的节点的父节点是黑色。
处理方法:什么也不需要做。节点被插入后,仍然是红黑树。 - ③ 情况说明:被插入的节点的父节点是红色。这种情况下,被插入节点是一定存在非空祖父节点的;进一步的讲,被插入节点也一定存在叔叔节点(即使叔叔节点为空,我们也视之为存在,空节点本身就是黑色节点)。理解这点之后,我们依据"叔叔节点的情况",将这种情况进一步划分为 3种情况(Case)
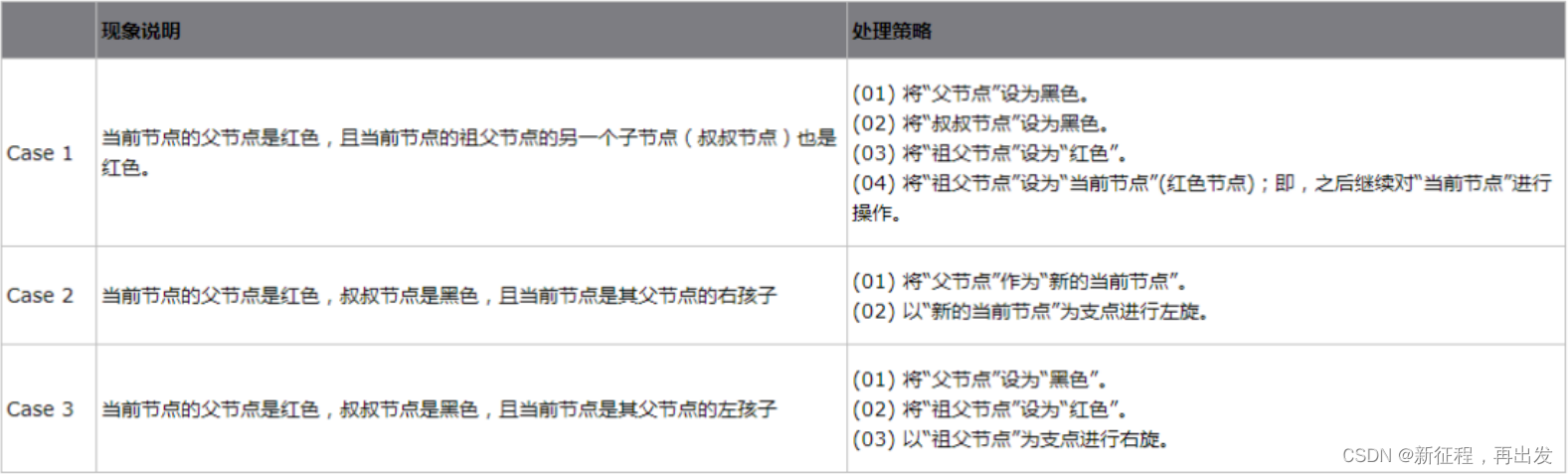
- ① 情况说明:被插入的节点是根节点。
- 第三步: 通过一系列的旋转或着色等操作,使之重新成为一颗红黑树。
删除
- 第一步:将红黑树当作一颗二叉查找树, 将节点删除。
这和"删除常规二叉查找树中删除节点的方法是一样的"。分 3 种情况:- ① 被删除节点没有儿子,即为叶节点。那么,直接将该节点删除就 OK 了。
- ② 被删除节点只有一个儿子。那么,直接删除该节点,并用该节点的唯一子节点顶替它的位置。
- ③ 被删除节点有两个儿子。那么,先找出它的后继节点;然后把“它的后继节点的内容”复制给“该节点的内容”;之后,删除“它的后继节点”。
- 第二步:通过"旋转和重新着色"等一系列来修正该树,使之重新成为一棵红黑树。
因为"第一步"中删除节点之后,可能会违背红黑树的特性。所以需要通过"旋转和重新着色"来修正该树,使之重新成为一棵红黑树。
选择重着色 3 种情况。- ① 情况说明: x 是“红+黑”节点。
处理方法:直接把 x 设为黑色,结束。此时红黑树性质全部恢复。 - ② 情况说明: x 是“黑+黑”节点,且 x 是根。
处理方法:什么都不做,结束。此时红黑树性质全部恢复。 - ③ 情况说明: x 是“黑+黑”节点,且 x 不是根。
处理方法:这种情况又可以划分为 4 种子情况。这 4 种子情况如下表所示:

- ① 情况说明: x 是“红+黑”节点。
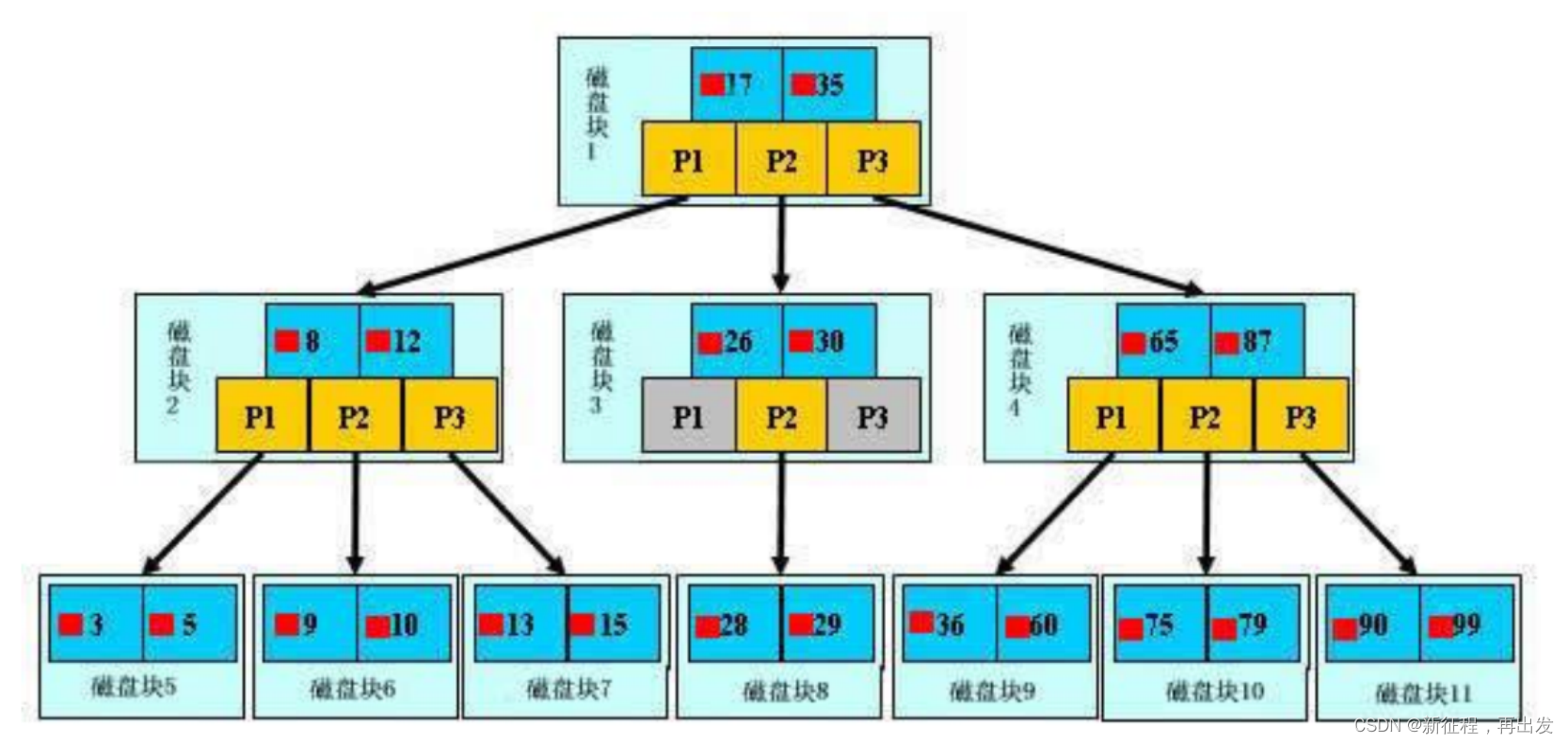
B-Tree
B-tree 又叫平衡多路查找树。一棵 m 阶的 B-tree (m 叉树)的特性如下(其中 ceil(x)是一个取上限的函数):
- 树中每个结点至多有 m 个孩子;
- 除根结点和叶子结点外,其它每个结点至少有有 ceil(m / 2)个孩子;
- 若根结点不是叶子结点,则至少有 2 个孩子(特殊情况:没有孩子的根结点,即根结点为叶子结点,整棵树只有一个根节点);
- 所有叶子结点都出现在同一层,叶子结点不包含任何关键字信息(可以看做是外部结点或查询失败的结点,实际上这些结点不存在,指向这些结点的指针都为 null); 5. 每个非终端结点中包含有 n 个关键字信息: (n, P0, K1, P1, K2, P2, …, Kn, Pn)。其中:
a) Ki (i=1…n)为关键字,且关键字按顺序排序 K(i-1)< Ki。
b) Pi 为指向子树根的接点,且指针 P(i-1)指向子树种所有结点的关键字均小于 Ki,但都大于 K(i-1)。
c) 关键字的个数 n 必须满足: ceil(m / 2)-1 <= n <= m-1。
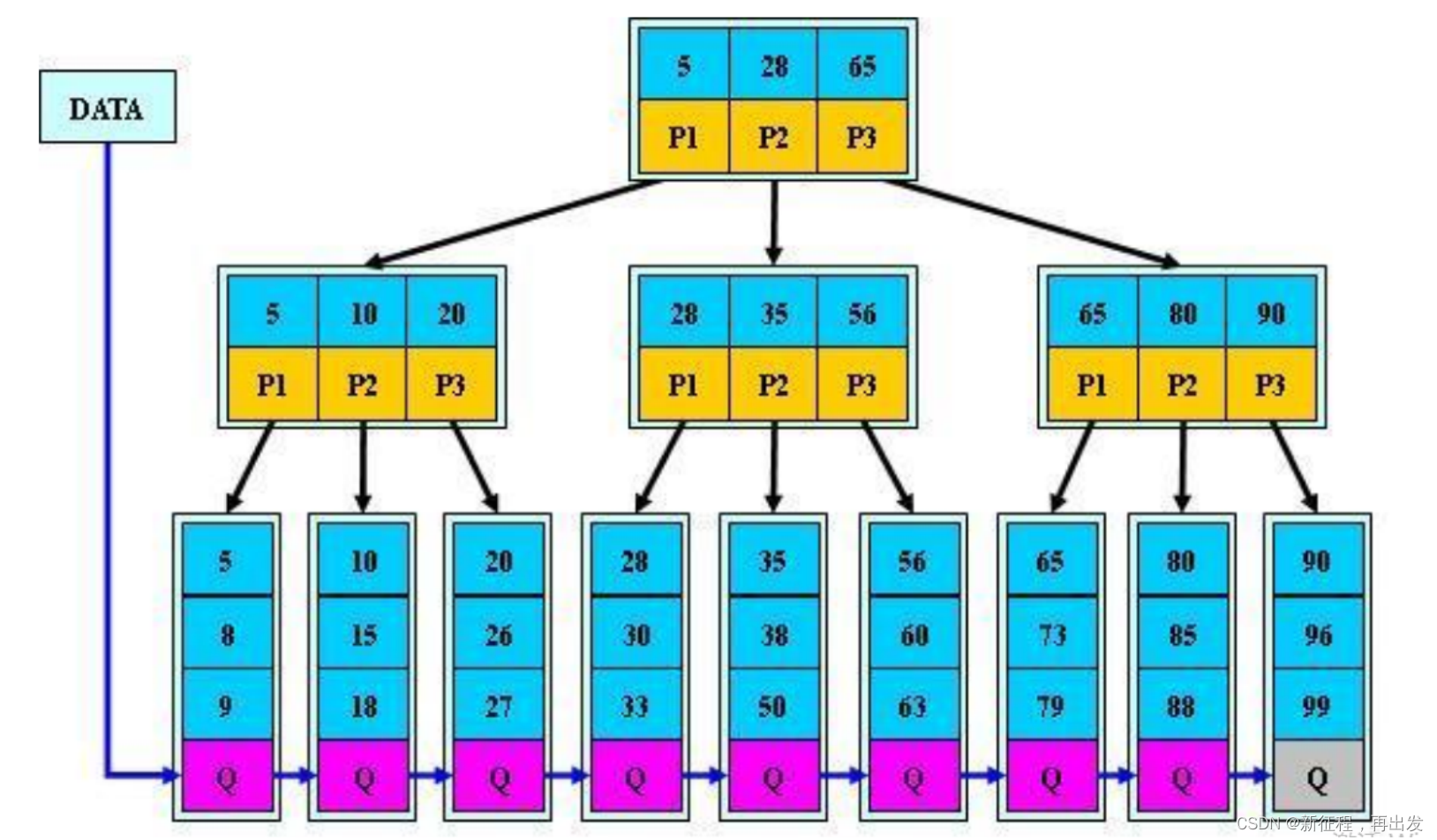
B+tree 和B-tree 的差异:
1.有 n 棵子树的结点中含有 n 个关键字; (B-tree 是 n 棵子树有 n-1 个关键字)
2.所有的叶子结点中包含了全部关键字的信息,及指向含有这些关键字记录的指针,且叶子结点本身依关键字的大小自小而大的顺序链接。 (B-tree 的叶子节点并没有包括全部需要查找的信息).
3.所有的非终端结点可以看成是索引部分,结点中仅含有其子树根结点中最大(或最小)关键字。(B-tree 的非终节点也包含需要查找的有效信息).
位图
位图的原理就是用一个 bit 来标识一个数字是否存在,采用一个 bit 来存储一个数据,所以这样可以大大的节省空间。 bitmap 是很常用的数据结构, 比如用于 Bloom Filter 中;用于无重复整数的排序等等。 bitmap 通常基于数组来实现,数组中每个元素可以看成是一系列二进制数,所有元素组成更大的二进制集合。
链接:https://www.cnblogs.com/polly333/p/4760275.html
结束!!!!!!
即使一动不动,时间也在替我们移动。而日子的消逝,就是带走我们希望保留的幻想。 ——罗曼·罗兰