Gang Scheduling Performance Benefits for Fine-Grain Synchronization

题目

• 什么是 gang secheduling ？ 组调度，要么一组全部执行，要么都不执行
• 什么是 fine-grain 同步 ？细粒度同步 CSDN 博客

摘要

• gang scheduling, where a set of threads are scheduled to execute simultaneously on a set of processors. gang scheduling 一组线程同时在一组处理器上执行的调度
• It allows the threads to interact efficiently by using busy waiting, without the risk of waiting for a thread that currently is not running 使用忙等来高效地互动。
• 否则使用 block 来达到同步地目的会造成上下文切换，造成很大的开销。
• have developed a model to evaluate the performance of different combi
  nations of synchronization mechanisms and scheduling policies 建立模型来评估同步机制和调度策略的组合
• gang schedule 在细粒度同步地要求下更高效

INTRODUCTION

• 随着“虚拟处理器”，多程序多处理器的发展， 程序执行过程中不可见，只能由系统软件管理 mapping 和 scheduling
• 并行应用的线程互动，体现在线程的同步上。
• explicit synchronization 显示同步 barrier 同步 互斥同步
• implicit synchronization 隐式同步，数据存在生产者和消费者关系等。
• In the case of fine-grain interactions it is shown that it is best for the threads to execute simultaneously on distinct processors，and to coordinate their activities with busy waiting.
  在细粒度的互动中，线程最好在不同的处理器上同时执行，通过忙等来进行协调
• 在粗粒度的同步中，如果执行时间的方差很大，最好是通过阻塞的方式进行同步。这样就可以将处理器让出来，将给其他线程执行。

Related work

这篇文章是第一个分析 gang scheduling 的性能，以及同步和调度之间相互作用的。

• This allows us to identify the situations in which gang scheduling
  should be used, namely when the application is based on fine-grain synchronization. 这也使我们能去确定，使用gang scheduling 的情况。

• It is also the first to report
  experiments based on a real implementation of gang scheduling on a multiprocessor. 他也是第一个真正基于多处理器上的组调度的实际实现的实验。

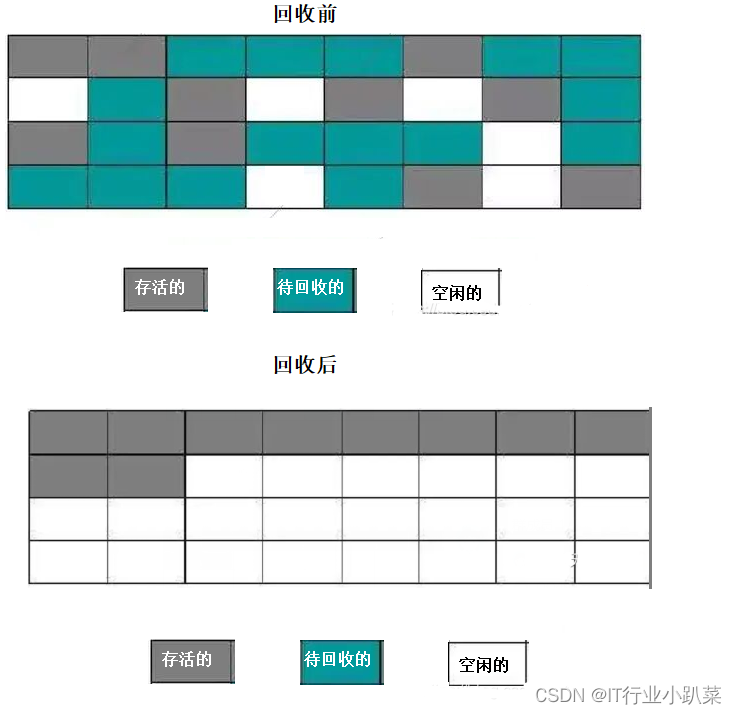
• Gang scheduling may cause an effect reminiscent of fragmentation, if the gang sizes do not fit the number of available processors. 如果组的大小和处理器数量不匹配，gang scheduling 将会产生 碎片效果

• In this paper we
  show that for fine-grain computations gang scheduling
  can more than double the processing capability. 在细粒度计算中，gang scheduling 可以将处理器的能力提高一倍以上。

• gang scheduling 指的就是将一组线程采用一对一的映射同时调度到一组处理器上。

2 Synchronization And Scheduling

• busy waiting ：忙等的性能非常依赖于系统的调度策略

• blocking

• Two-phase ：两阶段阻塞，第一阶段使用一段时间的忙等，然后使用阻塞。当和gang scheduling在细粒度的情况下使用，基本上只用到了第一阶段的 忙等。使用其他调度，基本上是blocking，并且还比blocking的开销更大。

• gang scheduling： 所用互动的线程同时运行，但是一组的线程数存在限制。

• uncoordinated scheduling：各个处理器上的线程单独调度。

gang scheduling 和 blocking 结合是没有意义的，因为blocking的线程就算切换上下文，让出了处理器，处理器还是不能切换给别的gang的线程。
所以有三种组合：

• busy waitng with gang scheduling
• busy waiting with uncoordinated scheduling
• blocking with uncoordinated scheduling

2.1 Model and Assumptions

• 线程执行迭代计算
• 每个迭代中执行 $t_p^{ij} $ 时间的计算，然后执行同步操作
• 在执行同步的时候，他也会xiao’hao’yi，由于每个线程都需要执行，直接将这一部分的开销计入 $t_p^{ij} $
• 每个线程，在执行一次迭代的时候，会有一个处理时间，和一个等待时间

平均等待时间
$$t_p=\frac{1}{nk}\sum _{i=1}^n\sum _{j=1}^k{t}_p^{ij}$$

$$t_p^{maxj}=ma{x}_{1\le i\le n}{t}_p^{ij}$$

迭代 j 的线程 i 的等待时间为

$$t_w^{ij}=t_p^{max,j}-t_p^{ij}$$

平均等待时间
$$t_w=\frac{1}{nk}\sum _{i=1}^n\sum _{j=1}^k{t}_w^{ij}$$

note:$t_p+t_w=(\frac{1}{k}){\sum }_{j=1}^k{t}_p^{maxj}$

由于同步的开销可能和处理器的数量相关，因此$t_p$ 的值还需要调整。

System Characterization

在多道程序多处理器的情况下，每个处理都映射了多个线程。并且，采用时分策略，为所有的线程提供相同的服务时间。
Assumptiong：

• the number of threads on each processor is denoted by l
• 我们只关注 a single gang of n threads ,mapped to n different processors,剩余的 n(l-1)个线程运行好坏不是我们关心的

对于blocking 策略，性能好坏，和其他gang 的线程行为有很大关系。因为blocking 策略有利他性：

1. 所有的线程的行为都相同，都执行迭代操作
2. 剩余的 l-1 组线程是独立调度的，纯计算的线程

调度时间片记为 ${\tau }_q$
上下文切换的开销记为 ${\tau }_{c}s$
blocking 的开销记为 $\alpha$ 倍的上下文开销， KaTeX parse error: Undefined control sequence: \aplpha at position 1: \̲a̲p̲l̲p̲h̲a̲ 一定是大于1的

在粗粒度的情况下：
$t_p$ 相对于 ${\tau }_q$可能会大的多，在执行同步步骤之前可能会执行许多个时间片

在细粒度的条件下：
$t_p$ 相对于 ${\tau }_q$可能小的多，假设${\tau }_q$的可能会执行 $10^4-10^5$ 个指令，每10-100个个指令执行一次交互。

$$k(t_p+t_w)\gg {\tau }_q$$
在细粒度情况下，k 要足够大

2.2 Performance Dervition

Busy Waiting with Gang Scheduling

执行k次迭代的时间为：

$$T=(k(t_p+t_w)+\frac{k(t_p+t_w)}{{\tau }_q}{\tau }_{cs})$$
乘 l 是因为，要考虑到每个processor 映射了 l个线程，并且采用了时分策略，需要为其他线程提供相同时长的服务。

平均每次迭代所需要的时间为：
$$t=(1+frac{\tau }_{cs}{\tau }_q)(t_q+t_w)l$$

因为 $t_p+t_w=(\frac{1}{k}){\sum }_{j=1}^k{t}_p^{maxj}$ ，所以执行速率取决于执行最慢的线程。

Busy Waiting with Uncoordinated Scheduling

使用忙等和非协调调度的行为表现和粒度是相关的。

粗粒度的情况下：
在粗粒度的情况下，Busy Waiting with Uncoordinated Scheduling与 gang scheduling 的行为几乎一样。
由于同一组的线程不必同时执行，会导致 $t_p+t_w$ 远远大于 ${\tau }_q$ ，每次迭代都会需要若干个调度。
计算 t 和之前的情况是一样的：
$$t=(1+frac{\tau }_{cs}{\tau }_q)(t_q+t_w)l$$

Question：

也是要等到所有线程同时调度时，才能完成同步操作的吧？ 所以 $t_w$ 的计算方式和之前不同？

在细粒度的情况下：
首先明确，在不加干预的情况下，也有一定概率，使得 n 个线程同时调度。当这种情况发生的时候，会完成很多轮的迭代。

当循环周期为 $\Lambda$时， n 段 长度为 $\lambda$ 的重叠为 $\frac{{\lambda }^n}{{\Lambda }^{n-1}}$

在细粒度的情况下 ：

• $\lambda {\tau }_q$
• $\Lambda =l({\tau }_q+{\tau }_{cs})$ 是一个调度周期
• 每个调度周期线程重叠时间为 $\frac{{\tau }_q^n}{l^{n-1}({\tau }_q+{\tau }_{cs}{)}^{n-1}}$
• 每个调度周期完成的迭代数为：$\frac{{\tau }_q^n}{l^{n-1}({\tau }_q+{\tau }_{cs}{)}^{n-1}(t_q+t_w)}$

执行 k 次迭代所需要的调度轮数 $m =\frac{kl^{n-1}(\tau_q + \tau_{cs})^{n-1}(t_q + t_w)}{\tau_q^n} $

总的执行时间为：

平均每一次迭代的时间为：

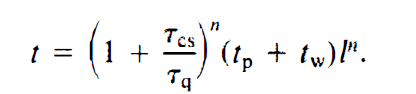
如果假设 ${\tau }_q\gg {\tau }_{cs}$,那么使用 uncoordinated 调度比 gang 调度慢 $l^{n-1}$倍

事实上，应满足每个调度周期至少完成一轮迭代。
$t=min(Eq.(8),({\tau }_q+{\tau }_{cs})l)$

Question: 为什么每个调度周期至少完成一轮迭代？他说这是个假设？没解释

Blocking Mechanism