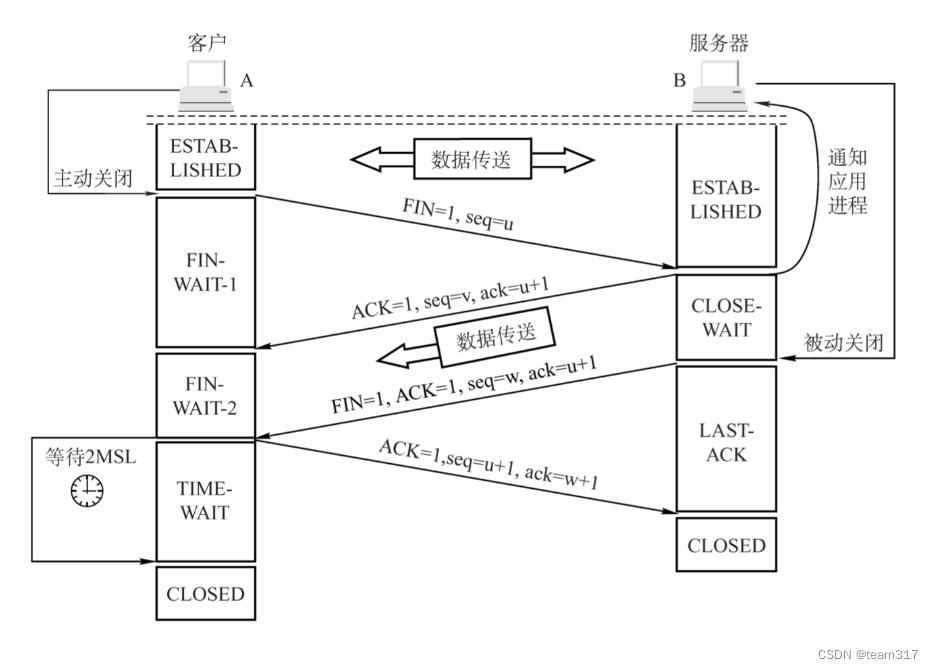
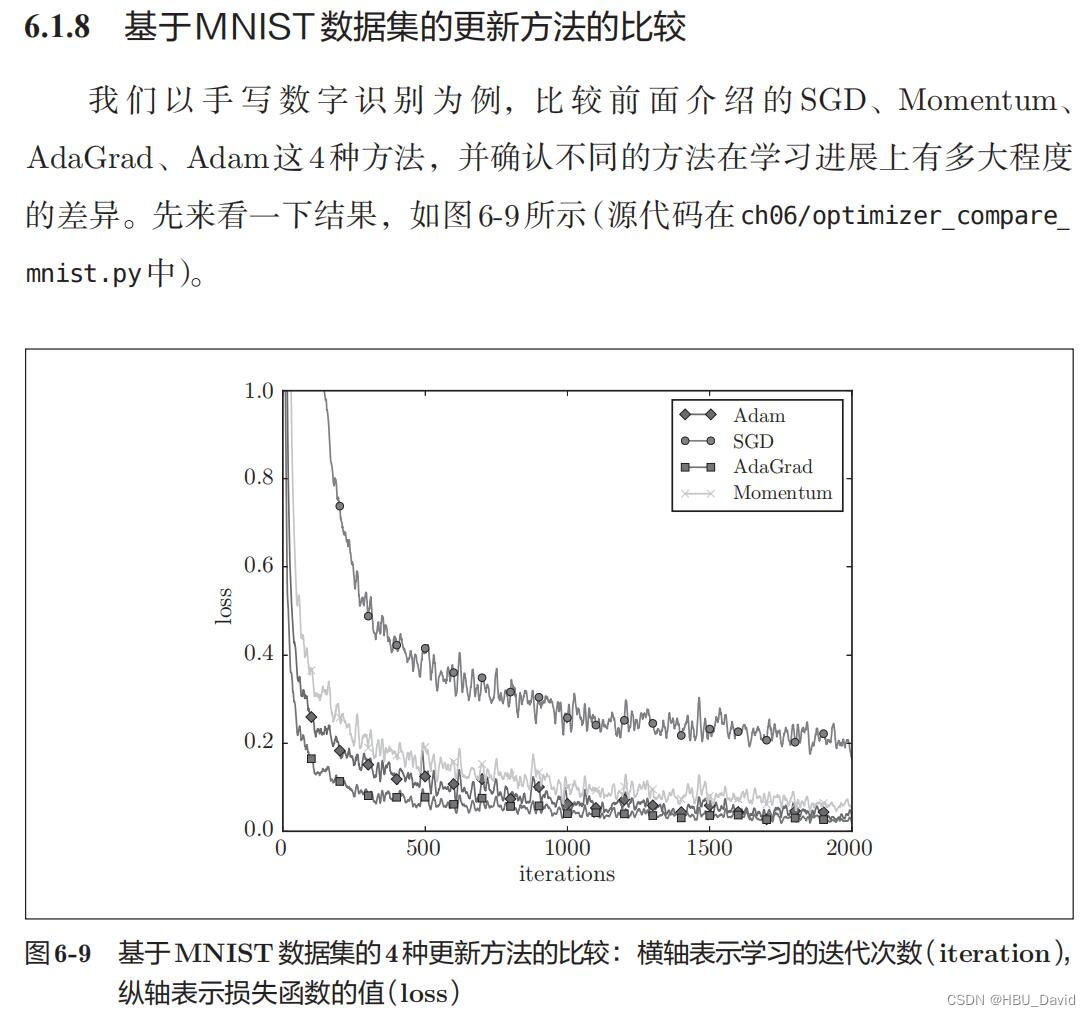
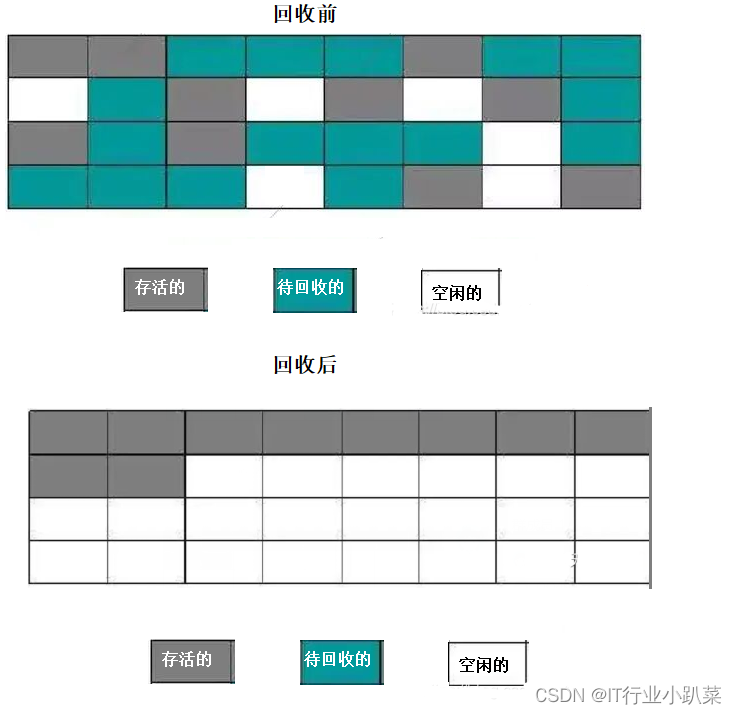
链接
- 点此跳转
思路
题目描述
有 n n n 个小朋友坐成一圈,每人有 a i a_i ai 颗糖果。
每人只能给左右两人传递糖果。每人每次传递一颗糖果的代价为 1 1 1 。
求使所有人获得均等糖果的最小代价。
分析
设 x i x_i xi 表示第 i i i 个朋友向第 i − 1 i-1 i−1 个小朋友给的糖果数量。如下图所示:
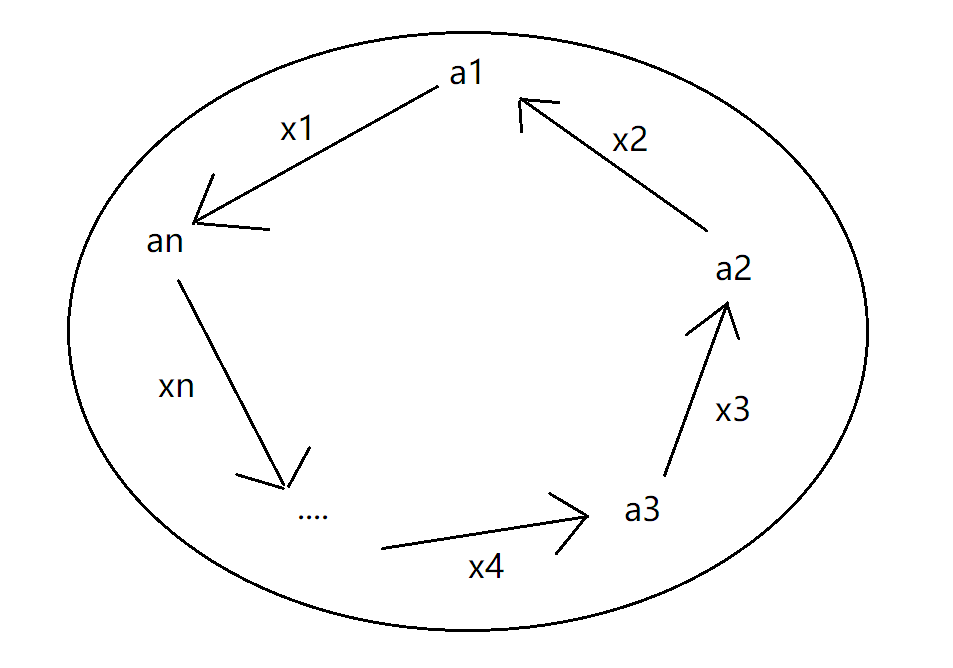
根据题目要求,我们的目标为下面的式子:
m
i
n
{
∣
x
1
∣
+
∣
x
2
∣
+
.
.
.
+
∣
x
n
∣
}
min\{|x_1| + |x_2| + ... + |x_n|\}
min{∣x1∣+∣x2∣+...+∣xn∣}
设平均数为
a
v
g
avg
avg 。可以列出来如下方程:
{
a
1
−
x
1
+
x
2
=
a
v
g
a
2
−
x
2
+
x
3
=
a
v
g
⋮
a
n
−
1
−
x
n
−
1
+
x
n
=
a
v
g
a
n
−
x
n
+
x
1
=
a
v
g
\left\{\begin{array}{c} a_{1}-x_{1}+x_{2}=a v g \\ a_{2}-x_{2}+x_{3}=a v g \\ \vdots \\ a_{n-1}-x_{n-1}+x_{n}=a v g\\ a_{n}-x_{n}+x_{1}=a v g \end{array}\right.
⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧a1−x1+x2=avga2−x2+x3=avg⋮an−1−xn−1+xn=avgan−xn+x1=avg
移项,将未知量放在左边:
{
x
1
−
x
2
=
a
1
−
a
v
g
x
2
−
x
3
=
a
2
−
a
v
g
⋮
x
n
−
1
−
x
n
=
a
n
−
1
−
a
v
g
x
n
−
x
1
=
a
n
−
a
v
g
\left\{ \begin{aligned} x_{1}-x_{2} &= a_{1}-avg\\ x_{2}-x_{3} &= a_{2}-avg \\ & \vdots \\ x_{n-1}-x_{n} &= a_{n-1}-avg \\ x_{n}-x_{1} &= a_{n}-avg \\ \end{aligned} \right.
⎩⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎧x1−x2x2−x3xn−1−xnxn−x1=a1−avg=a2−avg⋮=an−1−avg=an−avg
从倒数第二行一直到第一行累加到最后一行得到(最后一行不动),再移项得:
{
x
n
=
x
1
−
(
a
v
g
−
a
n
)
x
n
−
1
=
x
1
−
(
2
×
a
v
g
−
a
n
−
a
n
−
1
)
⋮
x
2
=
x
1
−
(
(
n
−
1
)
×
a
v
g
−
a
n
−
a
n
−
1
−
.
.
.
−
a
2
)
x
1
=
x
1
\left\{ \begin{aligned} x_{n} & =x_{1}-(avg-a_{n})\\ x_{n-1} & =x_{1}-(2\times avg-a_{n}-a_{n-1})\\ & \vdots \\ x_{2} & =x_{1}-((n-1)\times avg-a_{n}-a_{n-1}-...-a_{2})\\ x_{1} & = x_{1} \end{aligned} \right.
⎩⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎧xnxn−1x2x1=x1−(avg−an)=x1−(2×avg−an−an−1)⋮=x1−((n−1)×avg−an−an−1−...−a2)=x1
不妨设 x 1 x_1 x1 为自由变量,用 x 1 x_1 x1 表示其他变量。
观察 ∣ x n ∣ = ∣ x 1 − ( a v g − a n ) ∣ |x_n| = |x_1-(avg-a_n)| ∣xn∣=∣x1−(avg−an)∣ ,可知在数轴上表示 x 1 x_1 x1 到 a v g − a n avg-a_n avg−an 的距离,其余变量也同理。
问题就转变为给定数轴上一些点,找到一个点到所有点的距离和最小。
这个问题的结论为:
- 点的个数为奇数时,中间的点满足条件。
- 点的个数为偶数时,中间两个点都满足条件。
证明如下。
- 点的个数为奇数时
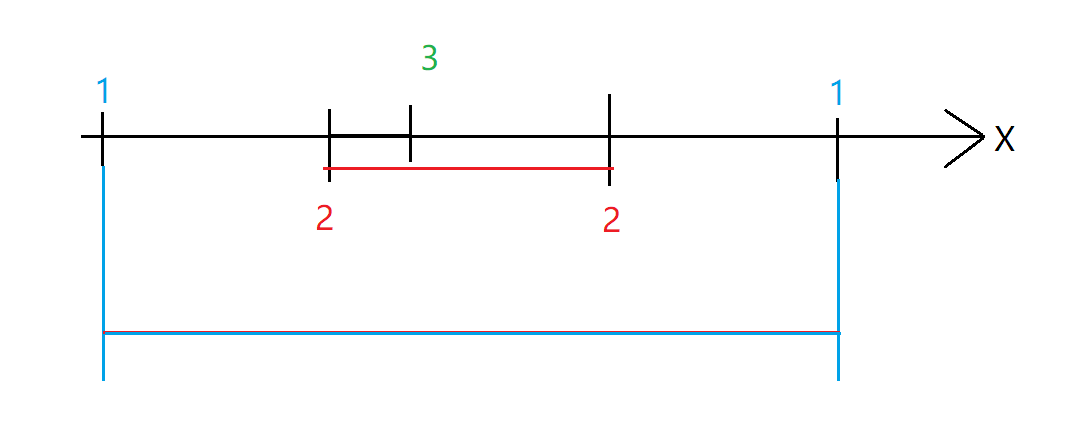
设最左边的点和最右边的点一组,依次这样两端为一组。
观察第 1 1 1 组,只有当点的取值在两点之间,到两点的距离之和最短。
- 因为若在两点之外,距离之和是两点距离 + 多出的距离。
- 所以只有在两点之间,到两点的距离之和为两点距离,也就是最短的。
同理,第 2 2 2 组,也是在两点之间的点,到两点的距离之和最短。
以此类推,可知 3 3 3 号点到所有点的距离之和最小,也就是中点。
- 点的个数为偶数时
证明类似点为奇数时。
总结
所以我们求出来所以数轴上的点 (设为 b b b ),取中点,计算距离。
b
b
b 可以递推得到:
b
i
=
b
i
+
1
+
a
v
g
−
a
i
b_{i} = b_{i + 1} + avg - a_{i}
bi=bi+1+avg−ai
AC代码
// #pragma GCC optimize(3)
#include <set>
#include <map>
#include <cmath>
#include <stack>
#include <queue>
#include <deque>
#include <cctype>
#include <string>
#include <cstdio>
#include <bitset>
#include <vector>
#include <cstdlib>
#include <cstring>
#include <sstream>
#include <iostream>
#include <algorithm>
// #include <unordered_set>
// #include <unordered_map>
#define endl '\n'
#define x first
#define y second
#define fi first
#define se second
#define PI acos(-1)
// #define PI 3.1415926
#define LL long long
#define INF 0x3f3f3f3f
#define lowbit(x) (-x&x)
#define PII pair<int, int>
#define ULL unsigned long long
#define PIL pair<int, long long>
#define all(x) x.begin(), x.end()
#define mem(a, b) memset(a, b, sizeof a)
#define rev(x) reverse(x.begin(), x.end())
#define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
using namespace std;
const int N = 1e6 + 10;
int n;
LL a[N], sum;
void solve() {
cin >> n;
for (int i = 1; i <= n; i ++ ) {
cin >> a[i];
sum += a[i];
}
sum /= n;
for (int i = n; i > 1; i -- ) {
a[i] = sum + a[i + 1] - a[i];
}
a[1] = 0;
sort(a + 1, a + 1 + n);
LL res = 0;
for (int i = 1; i <= n; i ++ ) res += abs(a[i] - a[(n + 1) / 2]);
cout << res << endl;
}
int main() {
IOS;
solve();
return 0;
}