---

前言

异构图注意力网络Heterogeneous Graph Attention Network ( HAN )学习笔记。

---

一、基础知识

1.异构图（Heterogeneous Graph）

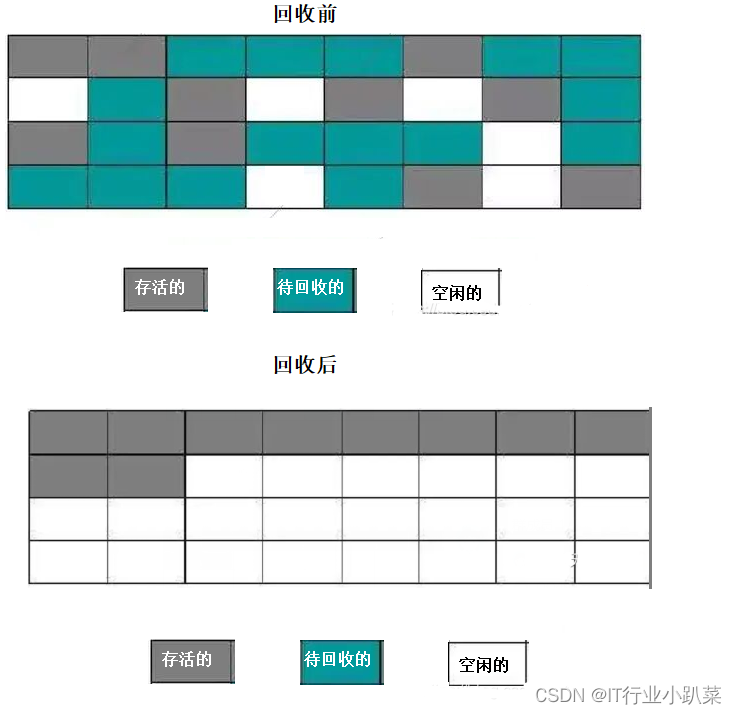
同构图是指结点类型相同、边类型也相同的图。异构图则是边和结点类型总和大于2的图，如下所示。

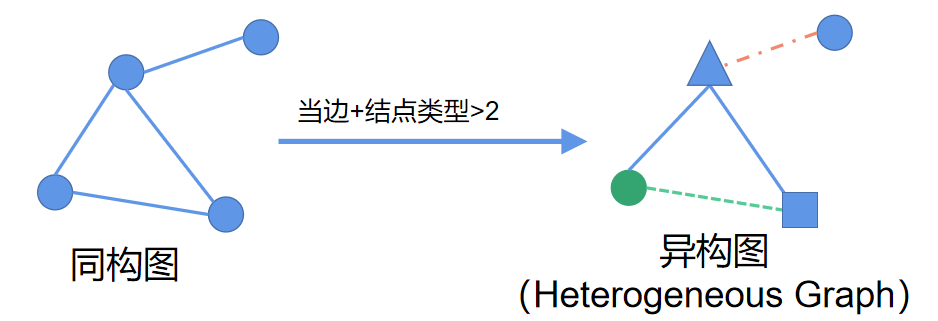
2.元路径

3.异构图注意力网络

中心思想：通过元路径生成不同元路径下的同构子图，在不同子图中进行消息传递聚合信息( Node-Level Attention )，最后将各元路径下子图聚合出的向量注意力加权聚合后进行后道传播( Sematic-Level Attention )。

为更清晰的解释原理，以下将逐步拆解。
（1）第一步

异构图如图片左边所示。根据M-A-M和M-D-M两种元路径，将有“介质”A或D连接的M之间视为通路（一阶邻居），可以拆解异构图为图片右边所示的子图。

二、异构图注意力网络

1.结点级别注意力（Node-level Attention）

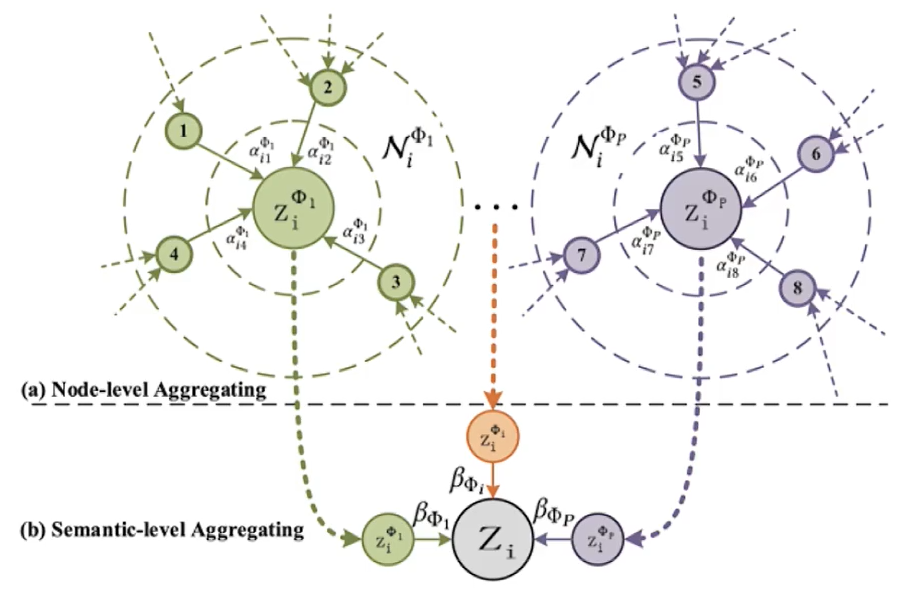
图取自论文原文

1. 节点注意力的计算。
   $${\mathbf{h}}_i^{\prime }={\mathbf{M}}_{{\varphi }_i}\cdot {\mathbf{h}}_i$$

• $i$为第i个主结点。
• $j$为第j个邻居结点。
• $M_{{\Phi }_i}$ 是模型需要训练的线性变化矩阵。 $M_{{\Phi }_i}$ 主要作用是提高拟合能力。
• ${\mathbf{h}}_i$为结点的特征向量。
  $${\alpha }_{ij}^{\Phi }={\mathrm{softmax}}_j\left(e_{ij}^{\Phi }\right)=\frac{\exp \left(\sigma \left({\mathbf{a}}_{\Phi }^{\mathrm{T}}\cdot \left[{\mathbf{h}}_i^{\prime }\Vert {\mathbf{h}}_j^{\prime }\right]\right)\right)}{{\sum }_{k\in {\mathcal{N}}_i^{\Phi }}\exp \left(\sigma \left({\mathbf{a}}_{\Phi }^{\mathrm{T}}\cdot \left[{\mathbf{h}}_i^{\prime }\Vert {\mathbf{h}}_k^{\prime }\right]\right)\right)}$$
• $N_i^{\Phi }$ 代表在元路径 $\Phi$ 下节点 $i$ 的邻居集。如图中左右两个$z_i^{\Phi }$周围的结点1、2、3…8
• $a_{ij}^{\Phi }$ 代表在元路径 $\Phi$ 下邻居节点 $j$ 传递消息至主节点 $i$ 的注意力。
• ${\alpha }_{\Phi }^T$ 是模型需要训练的线性变化矩阵， 更多的作用是调整形状。
• $||$为拼接符号。式子中是将两个节点的线性变换后的特征向量拼接起来。

2. 进行将注意力作为权重的加权求和计算(左边的公式), 或者多头注意力计算(右边的公式)。

$${\mathrm{z}}_i^{\Phi }=\sigma \left(\sum _{j\in {\mathcal{N}}_i^{\Phi }}{\alpha }_{ij}^{\Phi }\cdot {\mathbf{h}}_j^{\prime }\right){\mathrm{z}}_i^{\Phi }={\Vert }_{k=1}^K\sigma \left(\sum _{j\in {\mathcal{N}}_i^{\Phi }}{\alpha }_{ij}^{\Phi }\cdot {\mathbf{h}}_j^{\prime }\right)$$

• $z_i^{\Phi }$ 代表在元路径 $\Phi$ 下进行一轮消息传递后代表节点 $i$ 的特征向量。
• $\sigma$为激活函数。

2.语义级别注意力（Semantic-level Attention）

3. 语义级别注意力的计算。
   $$w_{{\Phi }_p}=\frac{1}{|\mathcal{V}|}\sum _{i\in \mathcal{V}}{\mathbf{q}}^{\mathrm{T}}\cdot \tanh \left(\mathbf{W}\cdot {\mathbf{z}}_i^{{\Phi }_p}+\mathbf{b}\right)$$

• $V$ 代表所有节点的数量。 $q,W,b$ 是此处模型需要训练的参数。
• 公式的意义代表对元路径 ${\Phi }^p$ 下生成的子图中所有的节点都进行 过消息传递得到每个节点的向量表示 $z_i^{{\Phi }_p}$ 后。进行线性变化再将 形状调整至一维标量后取个平均值。
• 对上述的结果进行Sotfmax归一化作为语义级别的注意力。
  $${\beta }_{{\Phi }_p}=\frac{\exp \left(w_{{\Phi }_p}\right)}{{\sum }_{p=1}^P\exp \left(w_{{\Phi }_p}\right)}$$

4. 最终注意力的加权求和。
   $$\mathbf{Z}=\sum _{p=1}^P{\beta }_{{\Phi }_p}\cdot {\mathbf{Z}}_{{\Phi }_p}$$

• 公式中的 $Z_{{\Phi }_P}$ 代表在元路径 $p$ 下生成的子图 ${\Phi }_p$ 的所有节点集合 $Z_{{\Phi }_P}={\left\{z_1^{{\Phi }_p},z_2^{{\Phi }_p}\dots z_n^{{\Phi }_p}\right\}}_{\circ }$
• $Z$ 即代表最终经过HAN网络层传递一轮后的节点特征向量集合 Z = { z 1 , z 2 … z n } Z=\left\{z_1, z_2 \ldots z_n\right\} Z={z1​,z2​…zn​} 。

---

总结