先说好，第八章不学。

学习目标

• 熟练掌握三次Bezier曲线
• 熟练掌握双三次Bezier曲面
• 熟练掌握B样条曲线
• 熟练掌握双三次B样条曲面

曲线与曲面的表示形式

---

插值与逼近

其实就是数学上的定义。

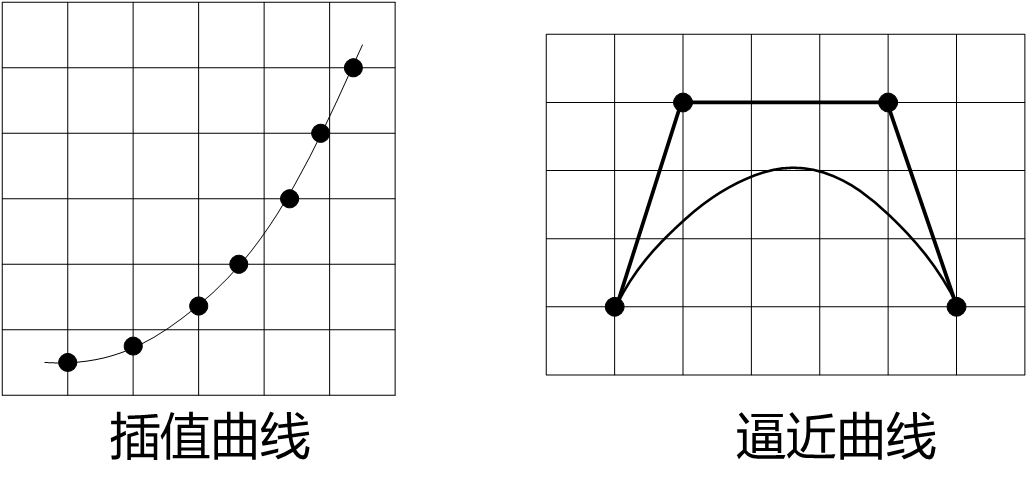
插值（Interpolation）：当用一组数据点来指定曲线的形状时，曲线精确地通过给定的数据点且形成光滑的曲线，称为曲线的插值。

逼近(Approximation)：当用一组控制点来指定曲线的形状时，曲线被每个控制点所吸引，但实际上并不经过这些控制点，称为曲线的逼近 。

插值与逼近统称为拟合（Fitting）。

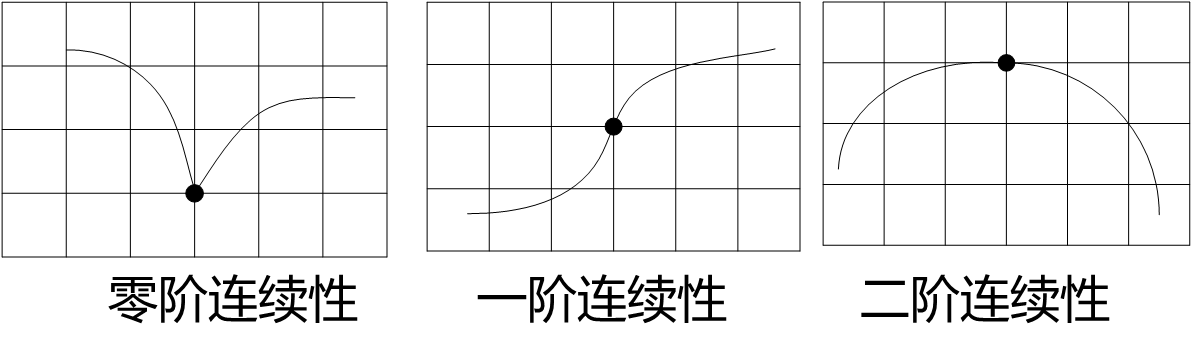
为了保证在连接点处光滑过渡，需要满足连续性条件。

Bezier曲线

定义

看最后的式子就行，。
在实际应用中，最常用的是三次Bezier曲线，其次是二次Bezier曲线，高次Bezier曲线一般很少使用。

void CTestView::DrawBezier()//绘制Bezier曲线
{
	CDC *pDC=GetDC();
	CPen NewPen,*pOldPen;
	NewPen.CreatePen(PS_SOLID,1,RGB(0,0,255));//曲线颜色
	pOldPen=pDC->SelectObject(&NewPen);	
	pDC->MoveTo(P[0]);
	for(double t=0.0;t<=1.0;t+=0.01)
	{		
		double x=0,y=0;
		for(int i=0;i<=n;i++)
		{
			x+=P[i].x*C(n,i)*pow(t,i)*pow(1-t,n-i);
			y+=P[i].y*C(n,i)*pow(t,i)*pow(1-t,n-i);
		}
		pDC->LineTo(Round(x),Round(y));
	}
	pDC->SelectObject(pOldPen);
	NewPen.DeleteObject();
	ReleaseDC(pDC);
}

double CTestView::C(const int &n, const int &i)//Bernstein第一项
{
	return double(Fac(n))/(Fac(i)*Fac(n-i));
}

long CTestView::Fac(int n)//阶乘函数
{
	int f;
	if(0==n||1==n)
		f=1;
	else
		f=n*Fac(n-1);
	return f;
}

//Power幂，Factorial阶乘

一次Bezier曲线

控制点P到底是坐标的形式还是其他表示形式目前还不知道。

---

二次Bezier曲线⭐⭐⭐

即使要拟合的是折线，Bezier曲线也是弯的。

---

三次Bezier曲线⭐⭐⭐

自由曲线：属于曲线的一种,形态变化自然,有较强的随意性,线的走向比较自由,没有明显的规律,变化比较丰富。

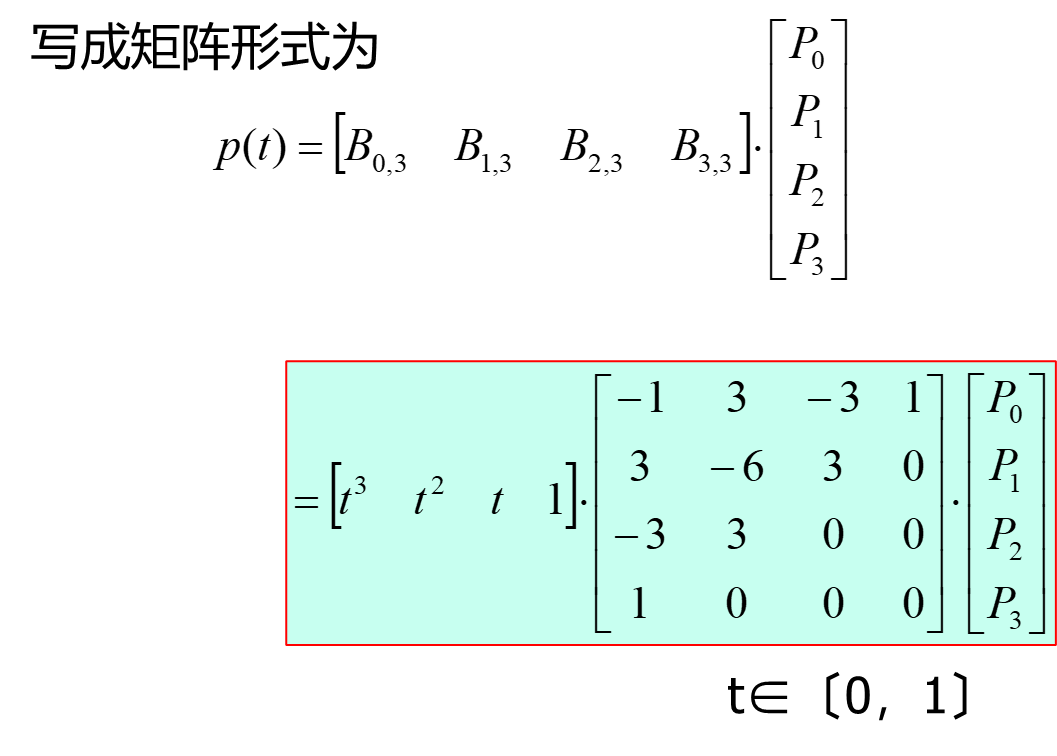
三次Bezier曲线的Bernstein基函数：

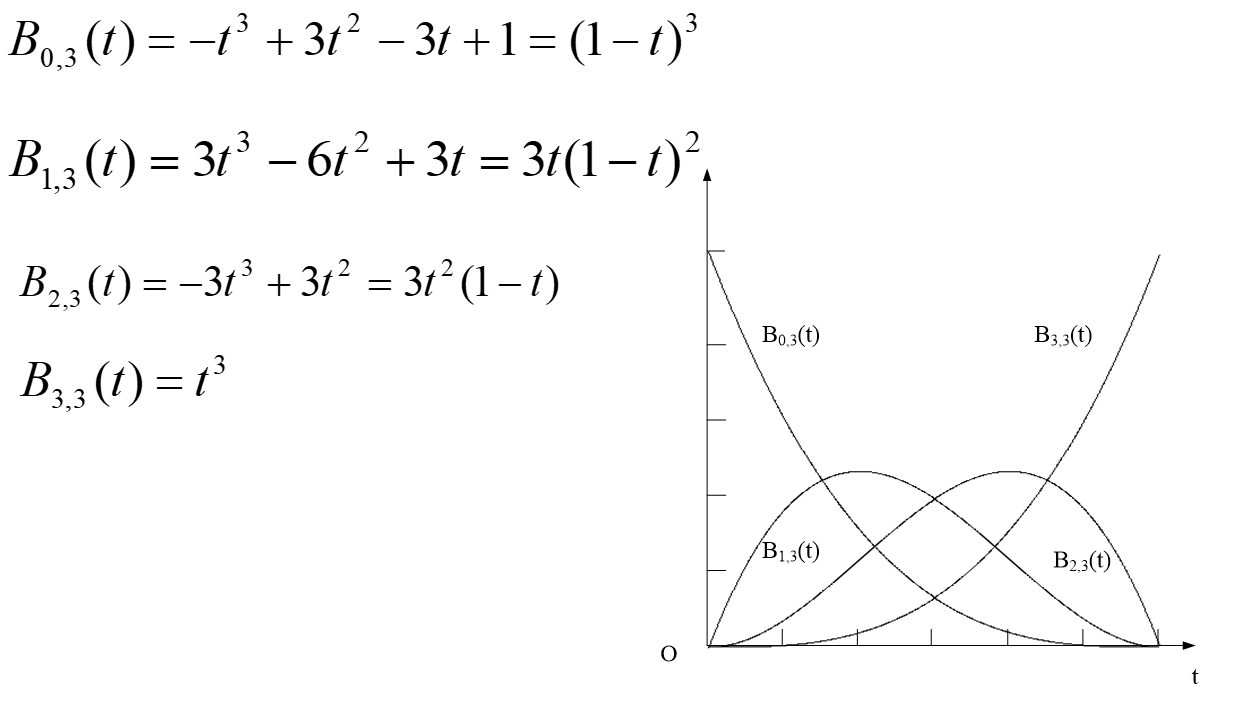
在区间〔0,1〕范围内，每个基函数均不为零，
说明不能使用控制多边形对曲线的形状进行局部调整，如果要改变某一控制点位置，整条曲线都将受到影响。

Bernstein基函数的性质

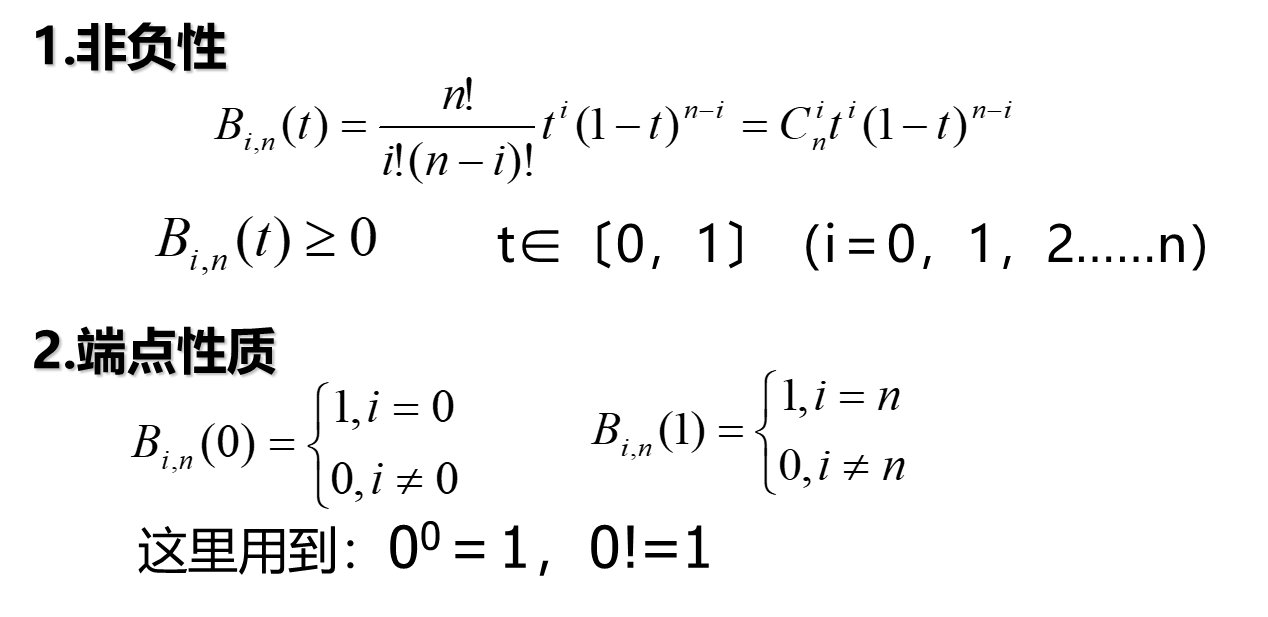
端点这里更像是起始点。

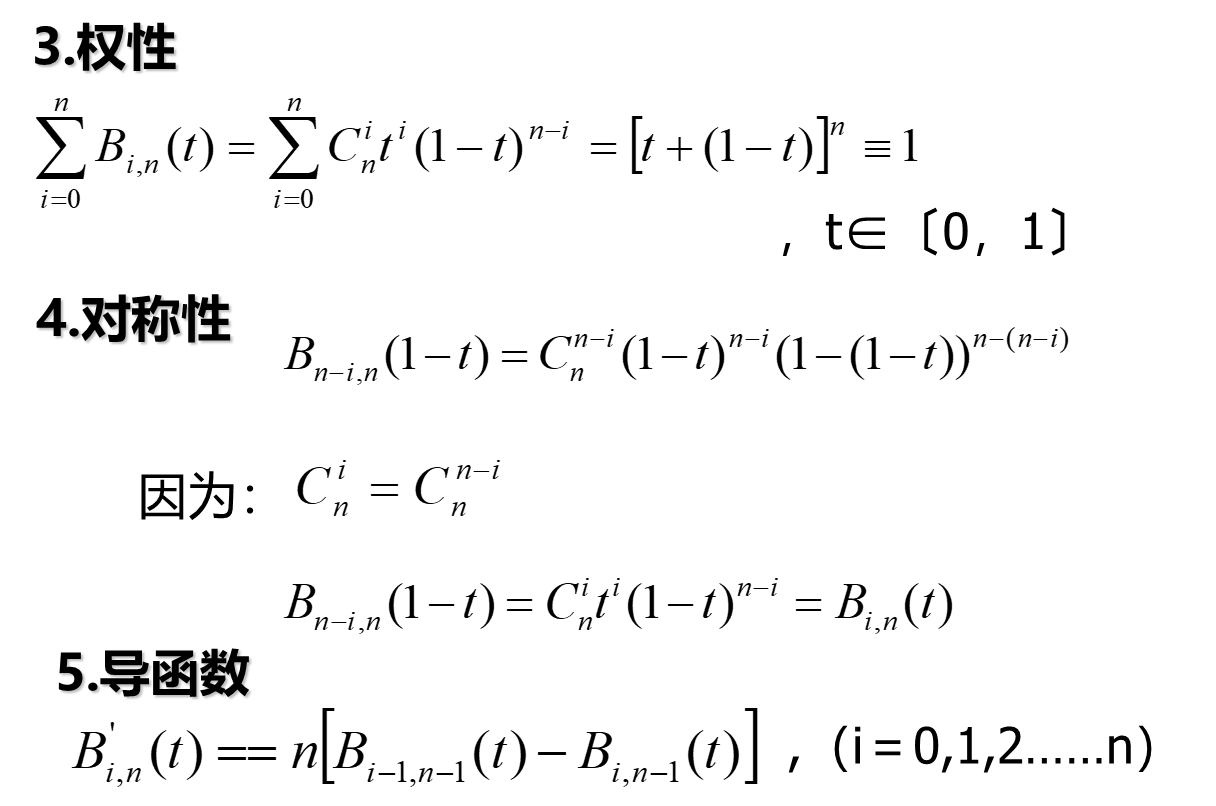
导函数推导过程：

Bezier曲线的性质

Bernstein基函数的性质决定了Bezier曲线的性质

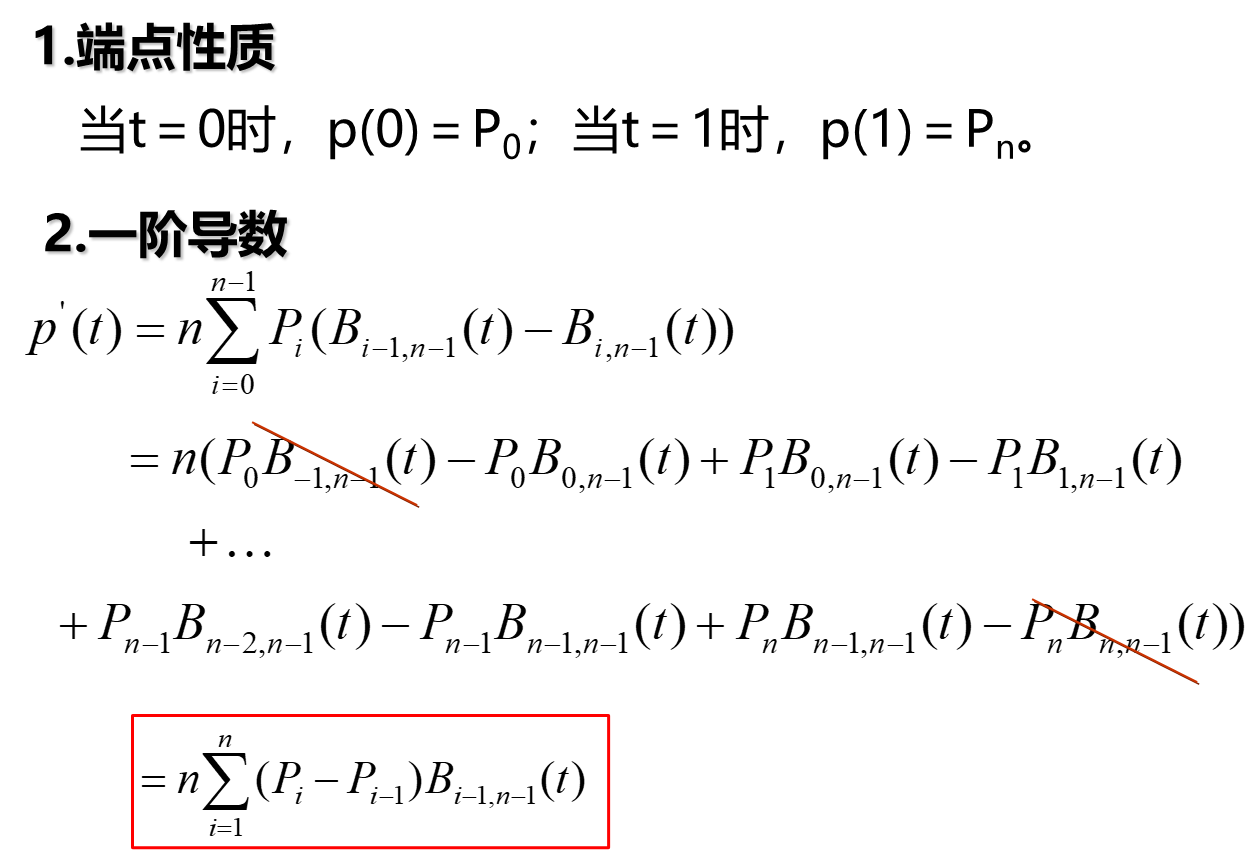
p的式子参考曲线的定义部分。
推导过程：

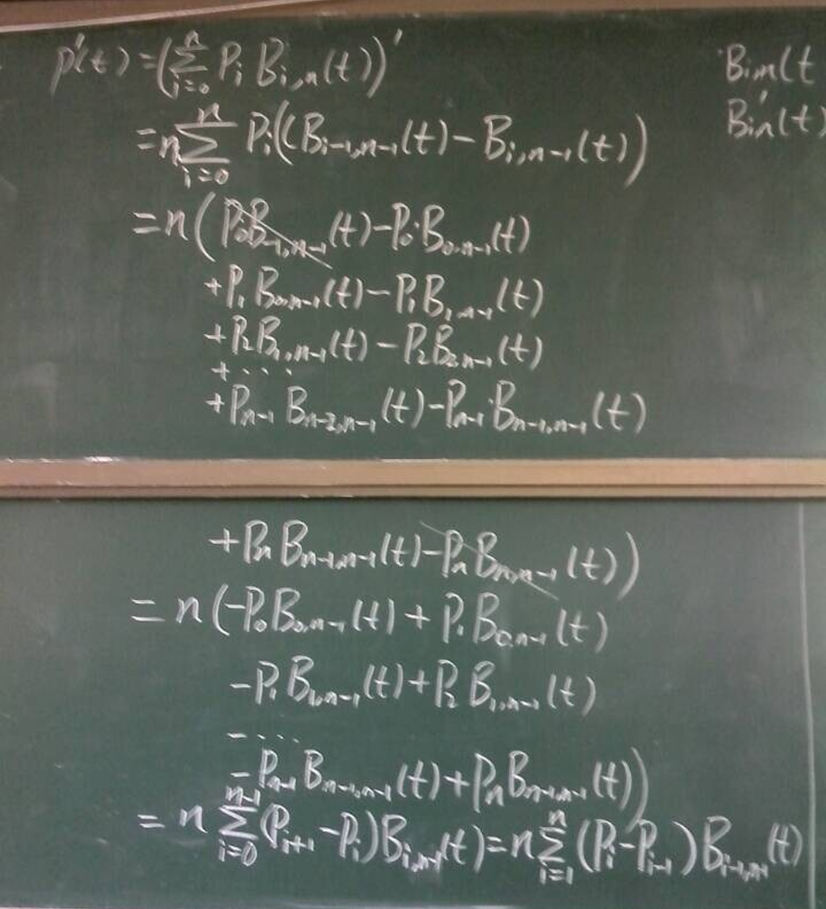
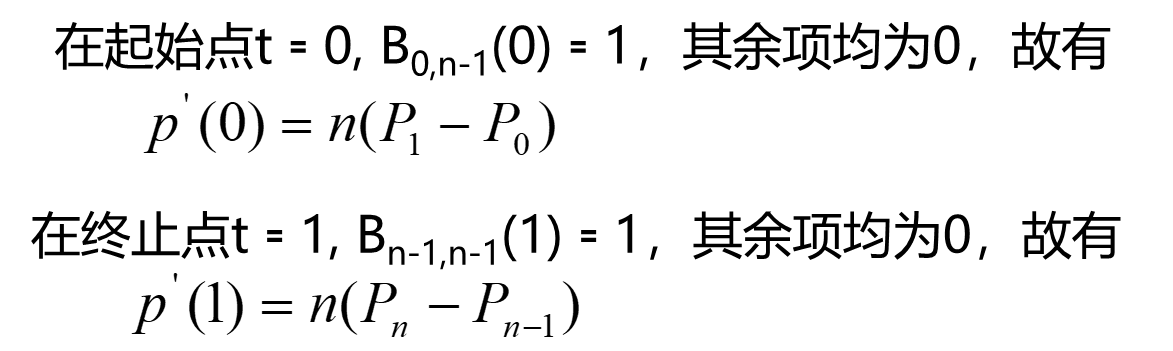
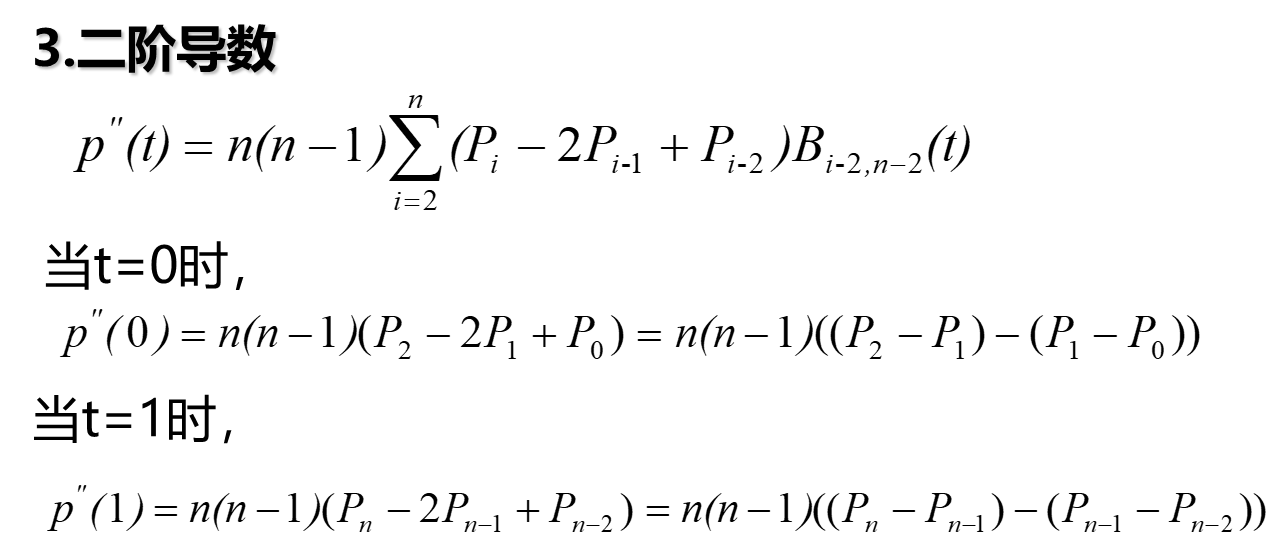
起始点和终止点的二阶导数分别取决于最开始的3个控制点和最后的3个控制点。

这个性质说明Bezier曲线在控制多边形的起点和终点上具有相同的性质

？？？曲线控制多边形？这里不对吧？

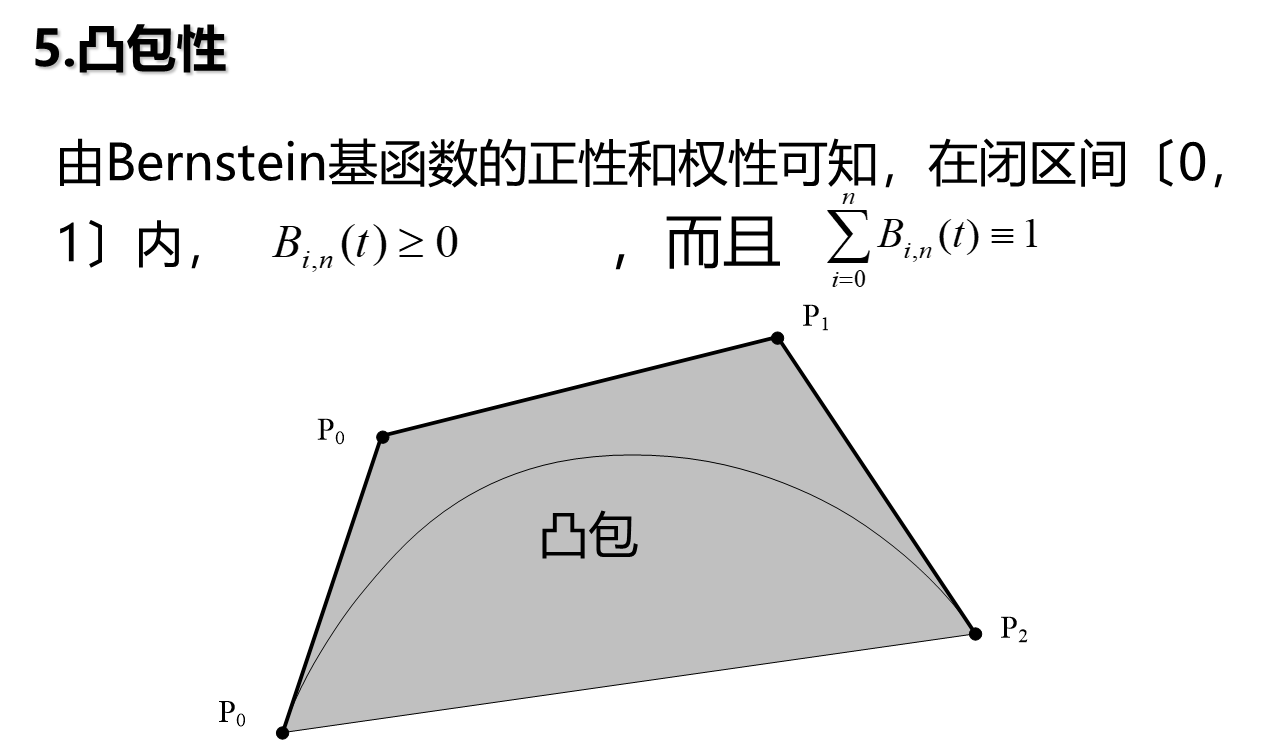
这说明Bezier曲线位于控制多边形构成的凸包之内，而且永远不会超出凸包的范围。

de Casteljau算法

Bezier曲线上的点，可以使用Bezier曲线方程直接计算，但使用de Casteljau递推算法则要简单的多。

几何作图法

r为递推次数，也是P的上标。

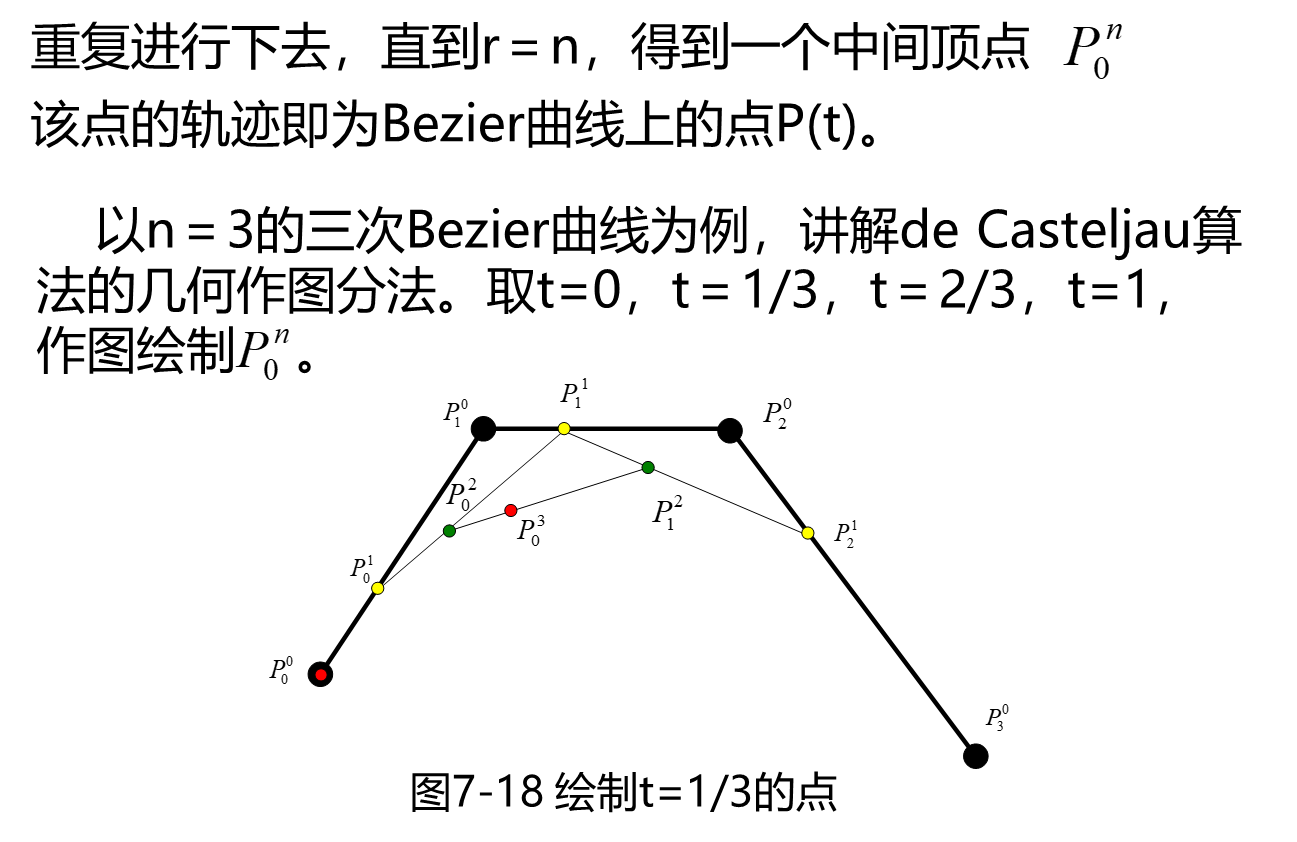
n是控制点P的个数减一。

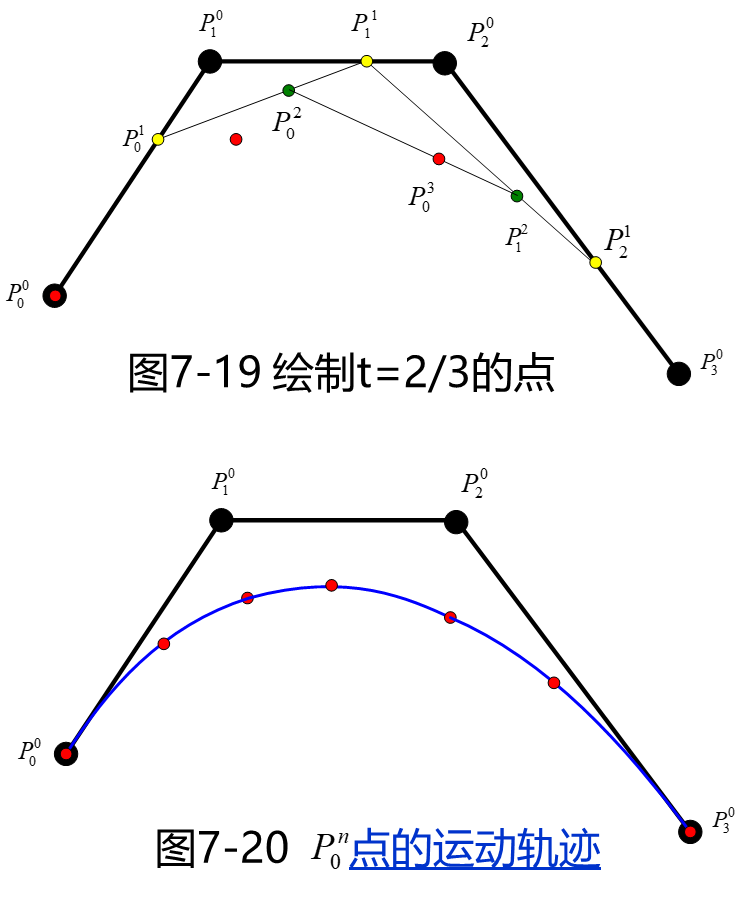
BUT！

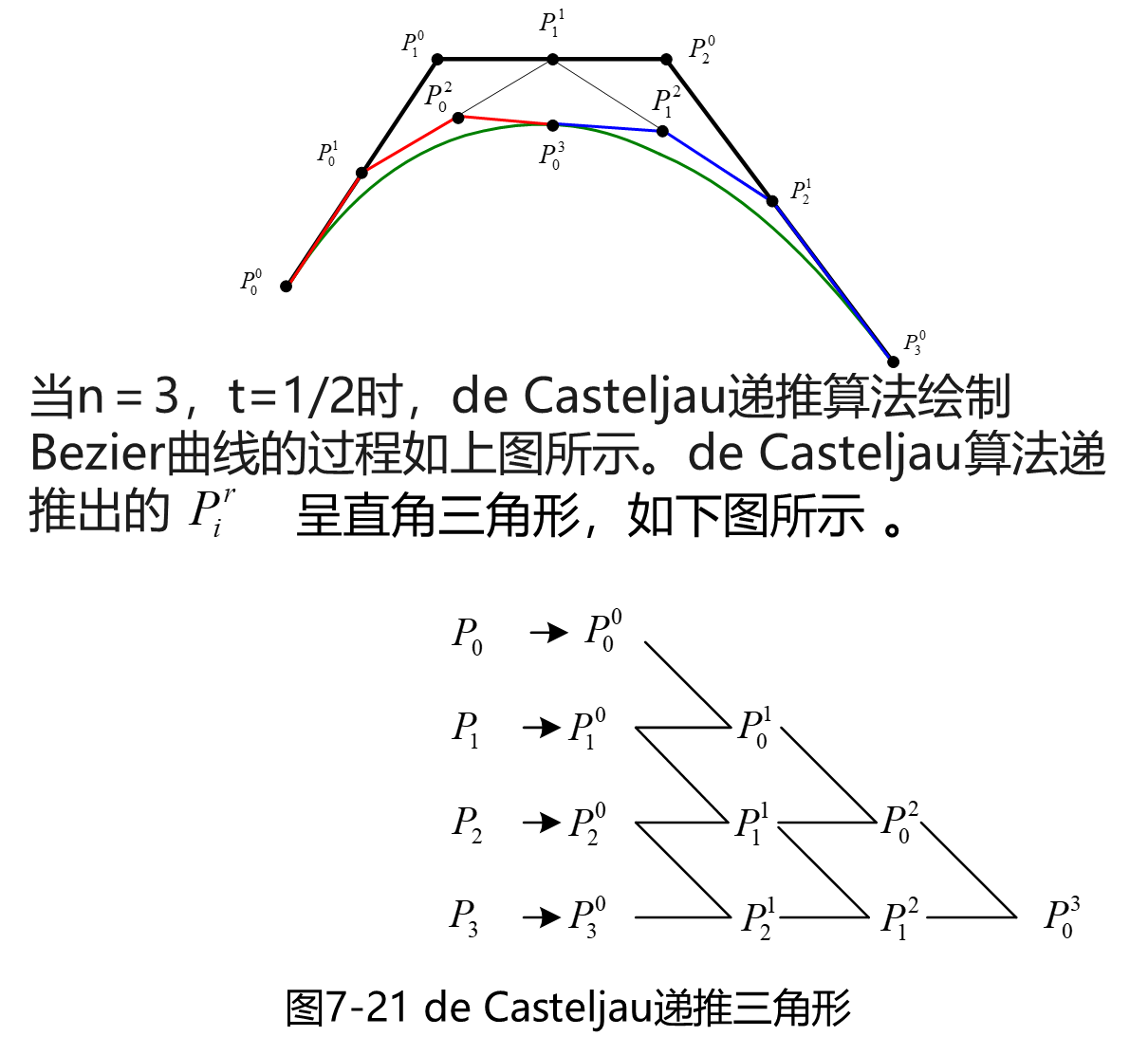
绘制Bezier曲线函数代码

void CTestView::DrawBezier()
{
	CDC* pDC=GetDC();
	pDC->MoveTo(P[0]);
	for(int k=0;k<=n;k++)
	{
		pt[k].x=P[k].x;
		pt[k].y=P[k].y;
	}
             for(double t=0.0;t<=1.0;t+=0.01)
	{
		deCasteljau(t,pt);
	    pDC->LineTo(Round(pp[0][n].x),Round(pp[0][n].y));
	
	}
	ReleaseDC(pDC);
}

de Casteljau函数代码

void CTestView::deCasteljau(double t,CP2 *p)
{
	for(int k=0;k<=n;k++)
	{
		pp[k][0]=p[k];
	}
	for(int r=1;r<=n;r++)//de Casteljau递推公式
	{
		for(int i=0;i<=n-r;i++)
		{ 
			pp[i][r].x=(1-t)*pp[i][r-1].x+t*pp[i+1][r-1].x;
			pp[i][r].y=(1-t)*pp[i][r-1].y+t*pp[i+1][r-1].y;
		} 
             } 
}

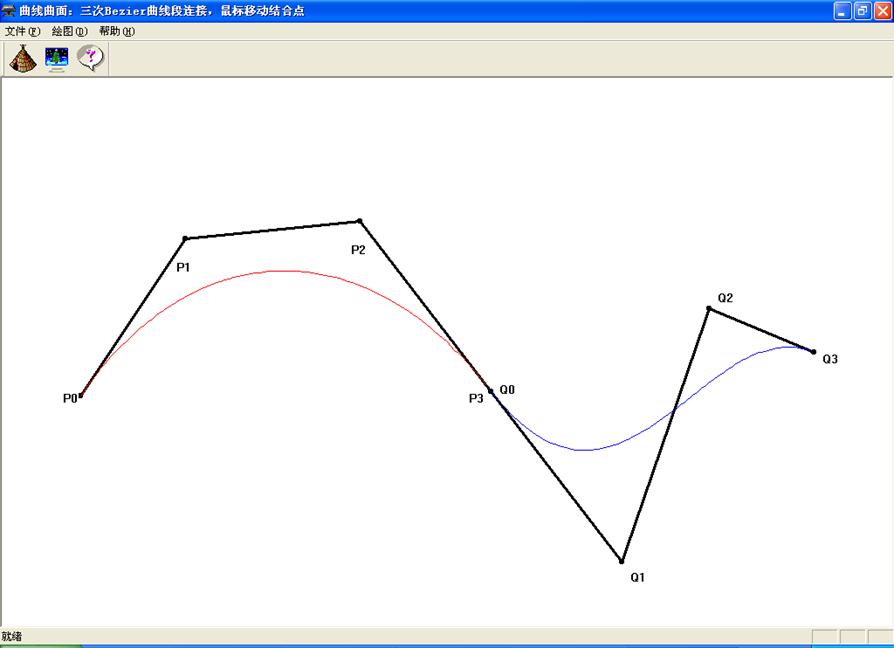
Bezier曲线的拼接

一条Bezier曲线往往难以描述复杂的曲面形状。这是由于增加控制多边形的顶点数，会引起Bezier曲线次数的提高，而高次Bezier曲线会带来计算上的困难。

工程中经常使用的是二次或三次Bezier曲线的拼接，要求在结合处满足一定的连续性条件。

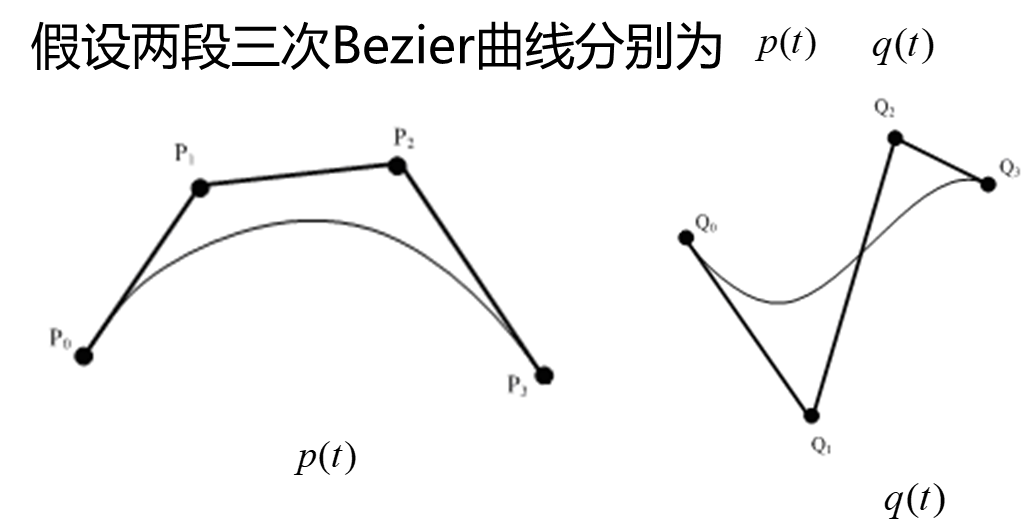
拼接后：

---

---

Bezier曲面

Bezier曲面的定义

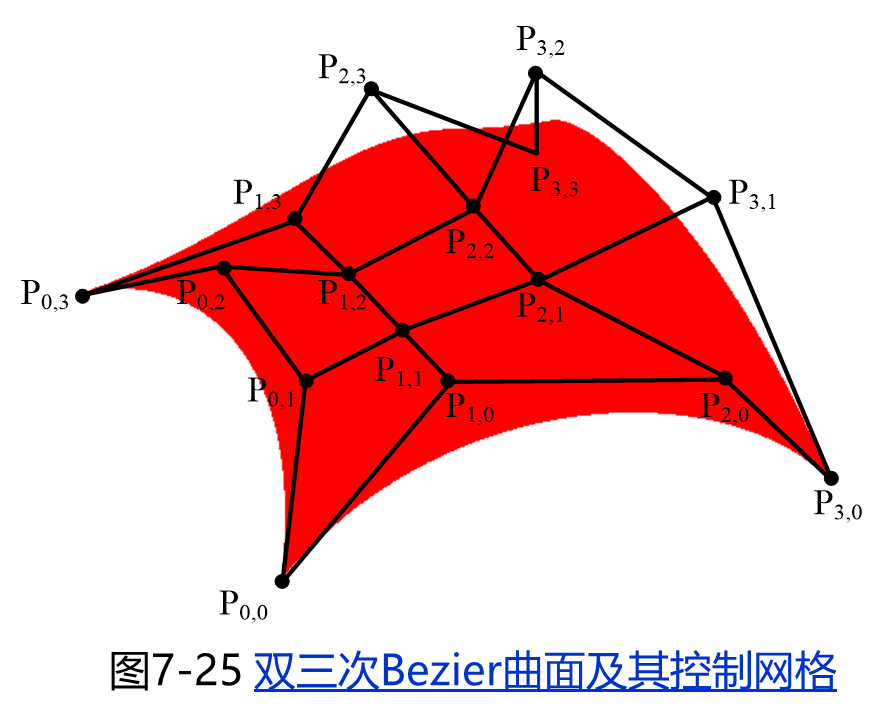
双三次Bezier曲面的定义

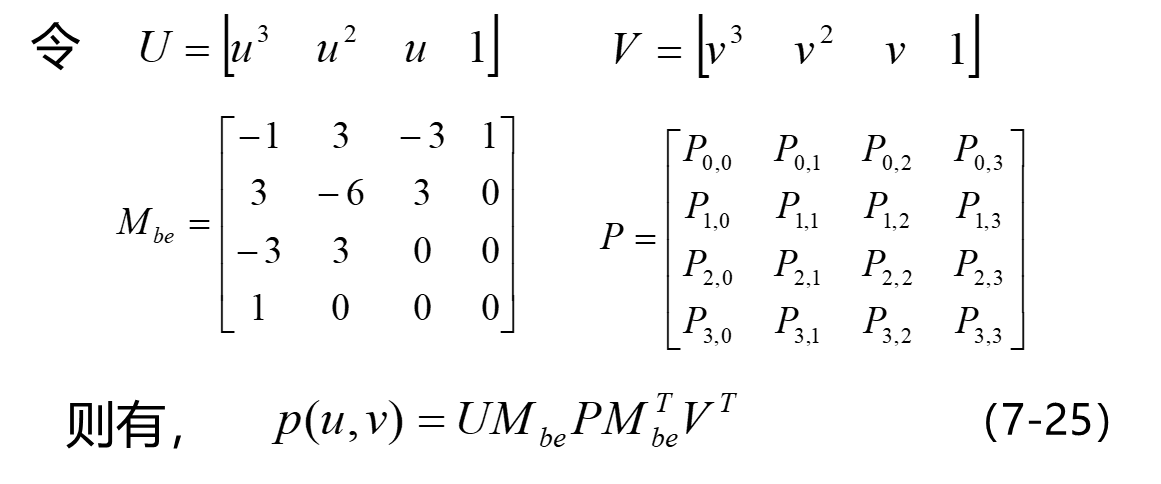
生成曲面时可以通过先固定u, 变化v得到一簇Bezier曲线；
然后固定v，变化u得到另一簇Bezier曲线，两簇曲线交织生成Bezier曲面。

双三次Bezier曲面的拼接

与Bezier拼接类似，两张双三次Bezier曲面片也可以拼接在一起。其Beizer曲面片表述如下:

**
**

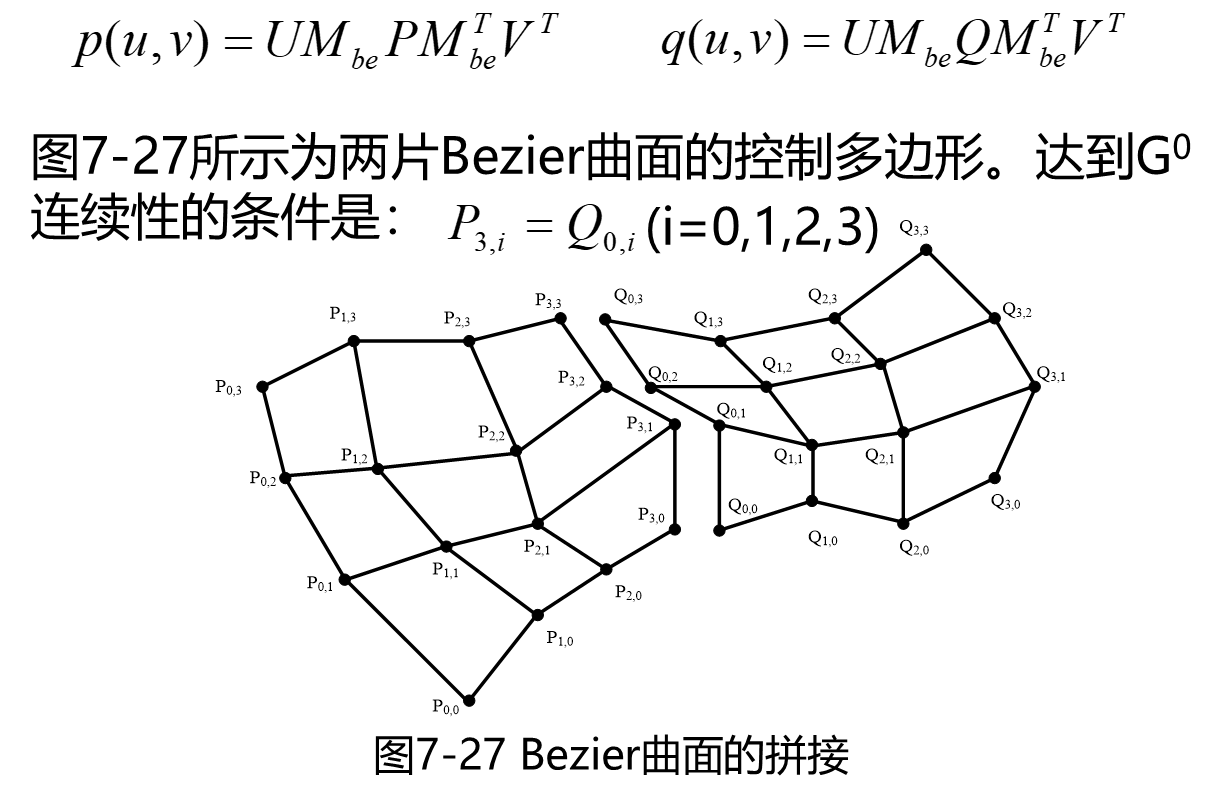
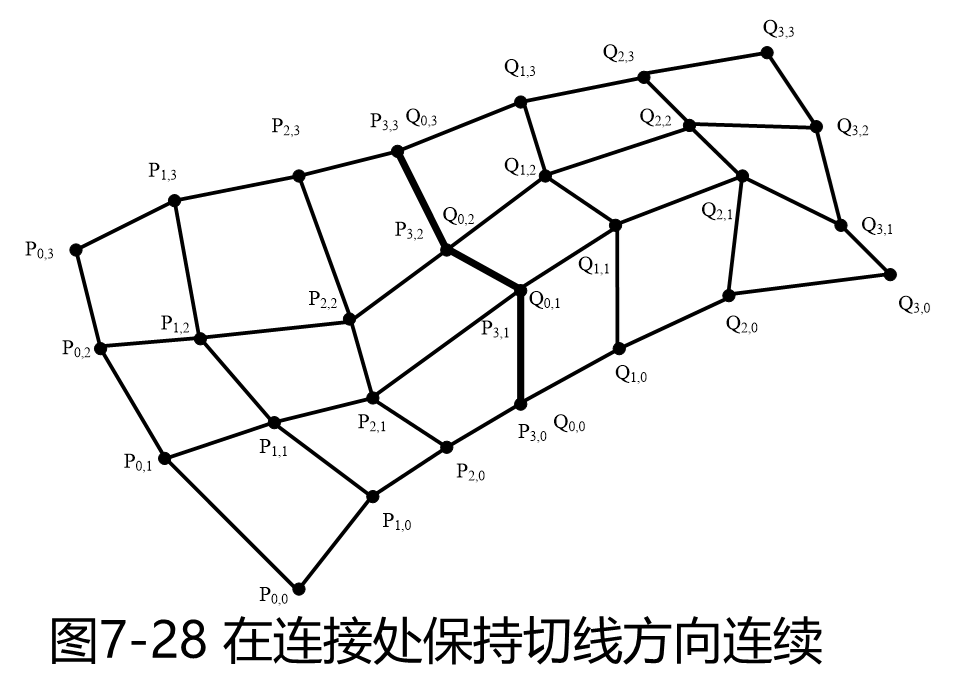
一般情况下，在连接处保持一阶导数连续较为困难，要求两个控制多边形中位于交点处的两条边必须共线，但设计中很难做到这一点。图7-28所示为满足G1连续性的条件的两片Bezier曲面的控制多边形。

B样条曲线

Bezier曲线虽然有许多优点，但也存在不足之处：

• 其一、确定了控制多边形的顶点个数为n+1个，也就确定了曲线的次数为n次；
• 其二、控制多边形与曲线的逼近程度较差，次数越高，逼进程度越差；
• 其三、曲线不能局部修改，调整某一控制点将影响到整条曲线，原因是Bernstein基函数在整个区间[0，1]内有支撑，所以曲线在区间内任何一点的值都将受到全部顶点的影响，调整任何控制点的位置，将会引起整条曲线的改变；
• 其四、Bezier曲线的拼接比较复杂。

为了解决上述问题，Gordon和Riesenfeld于1972年用B样条基函数代替了Bernstein基函数，构造了B样条曲线。

先有B样条基函数再有B样条曲线。

B样条曲线的定义

二次B样条曲线

二次B样条曲线的n＝2，k＝0，1，2。二次B样条曲线是二次多项式 。

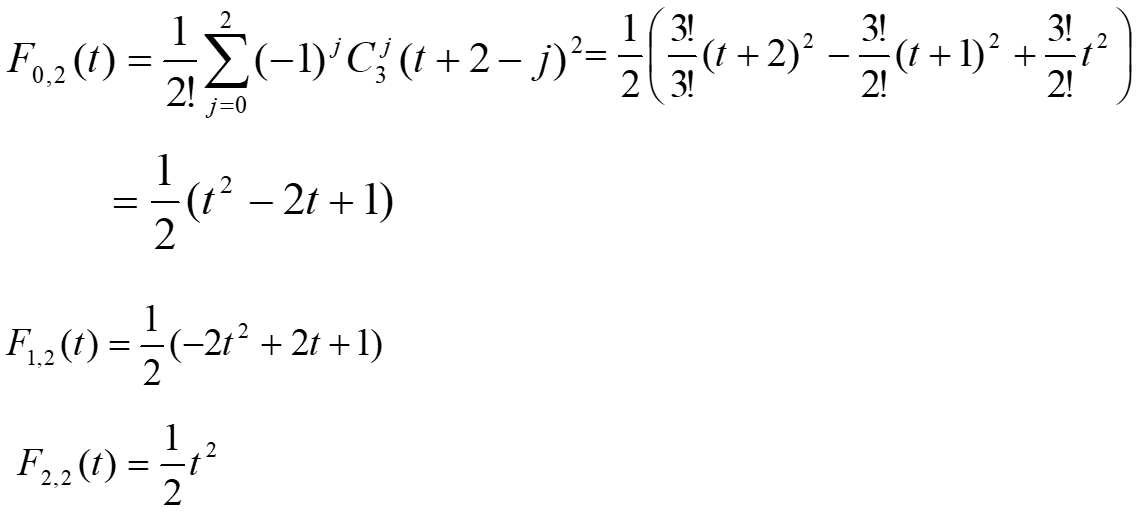
几何性质

其实这些都是矩阵表示，之不过在推演的时候用的算式。

三次B样条曲线

几何性质

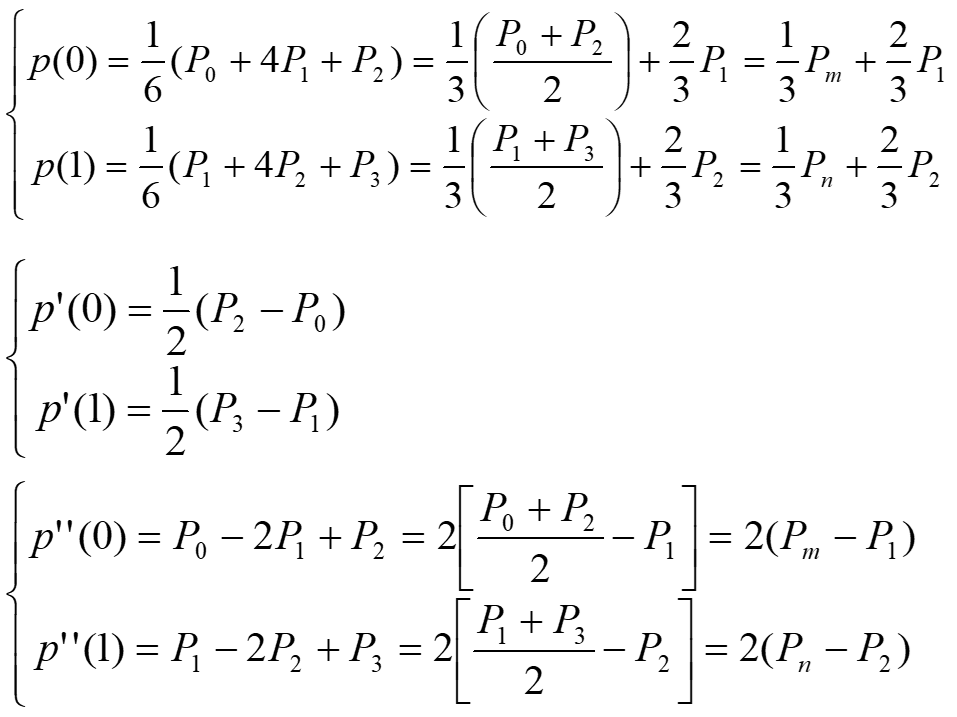
B样条曲线的性质

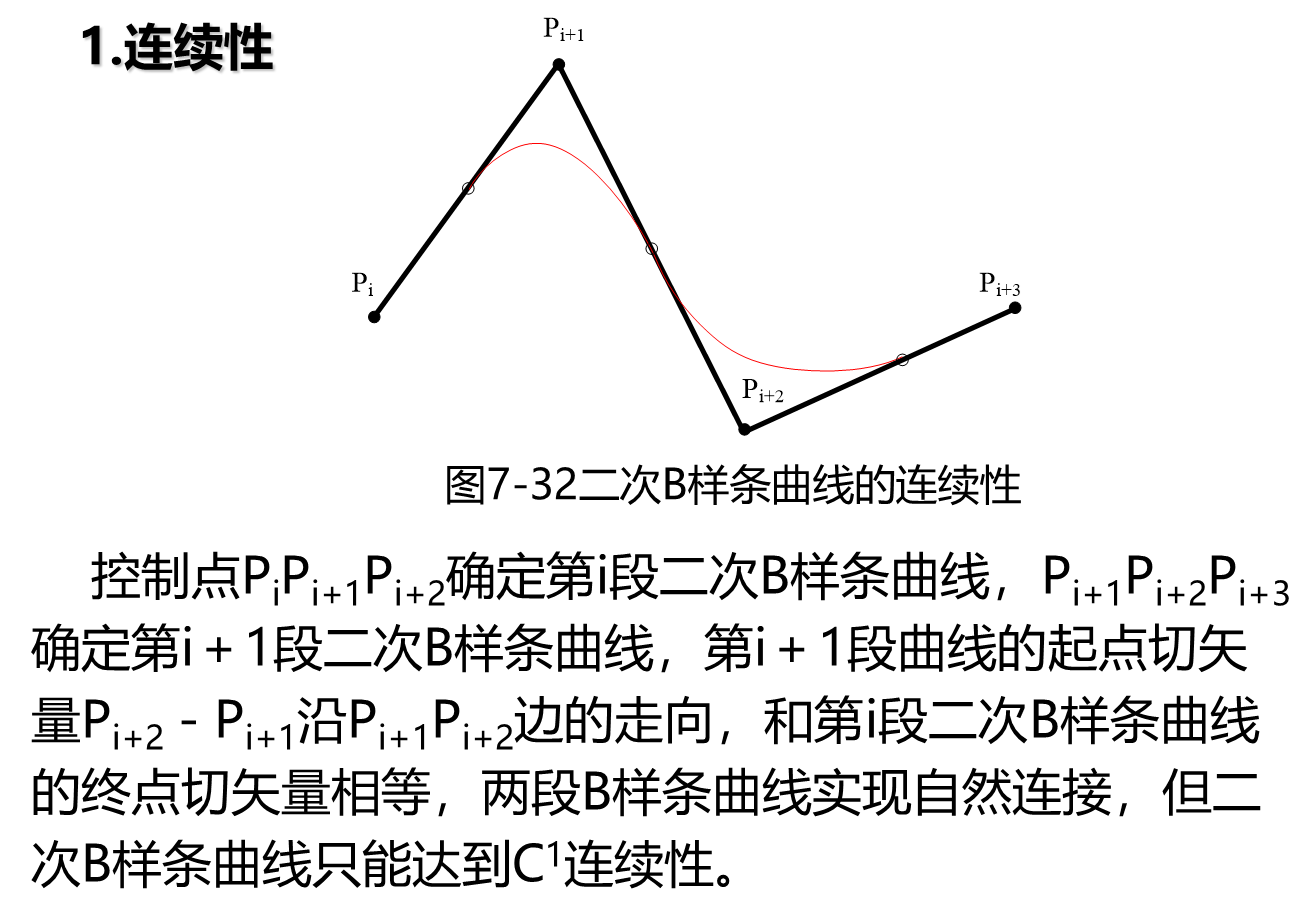
最后一句话是细节。

局部性质

在B样条曲线中，n次每段B样条曲线受n+1个控制点影响，改变一个控制点的位置，最多影响n+1个曲线段，其它部分曲线形状保持不变。

构造特殊的三次B样条曲线的技巧

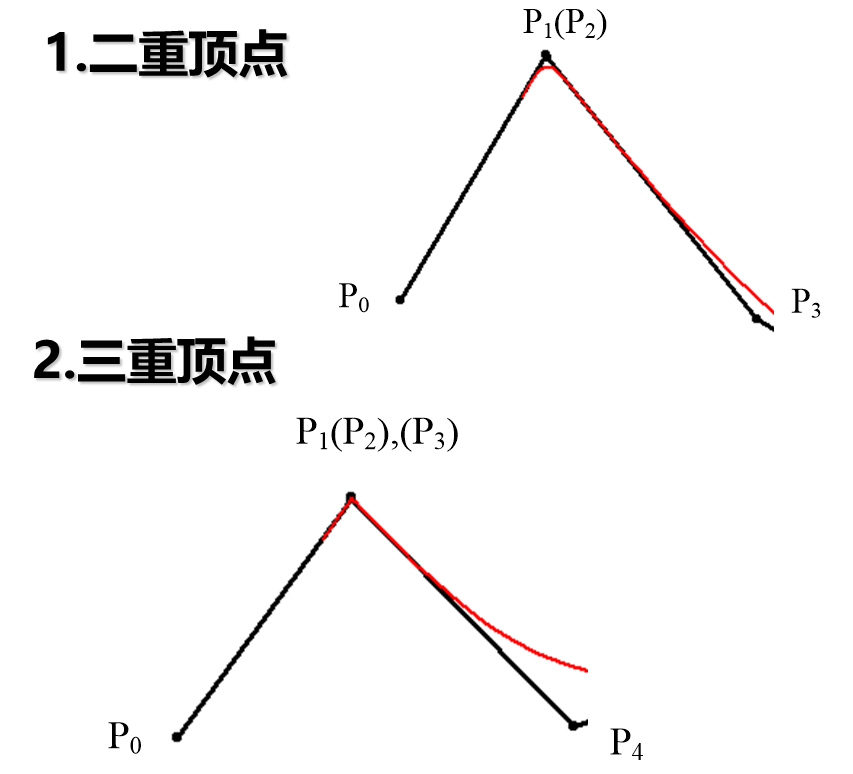
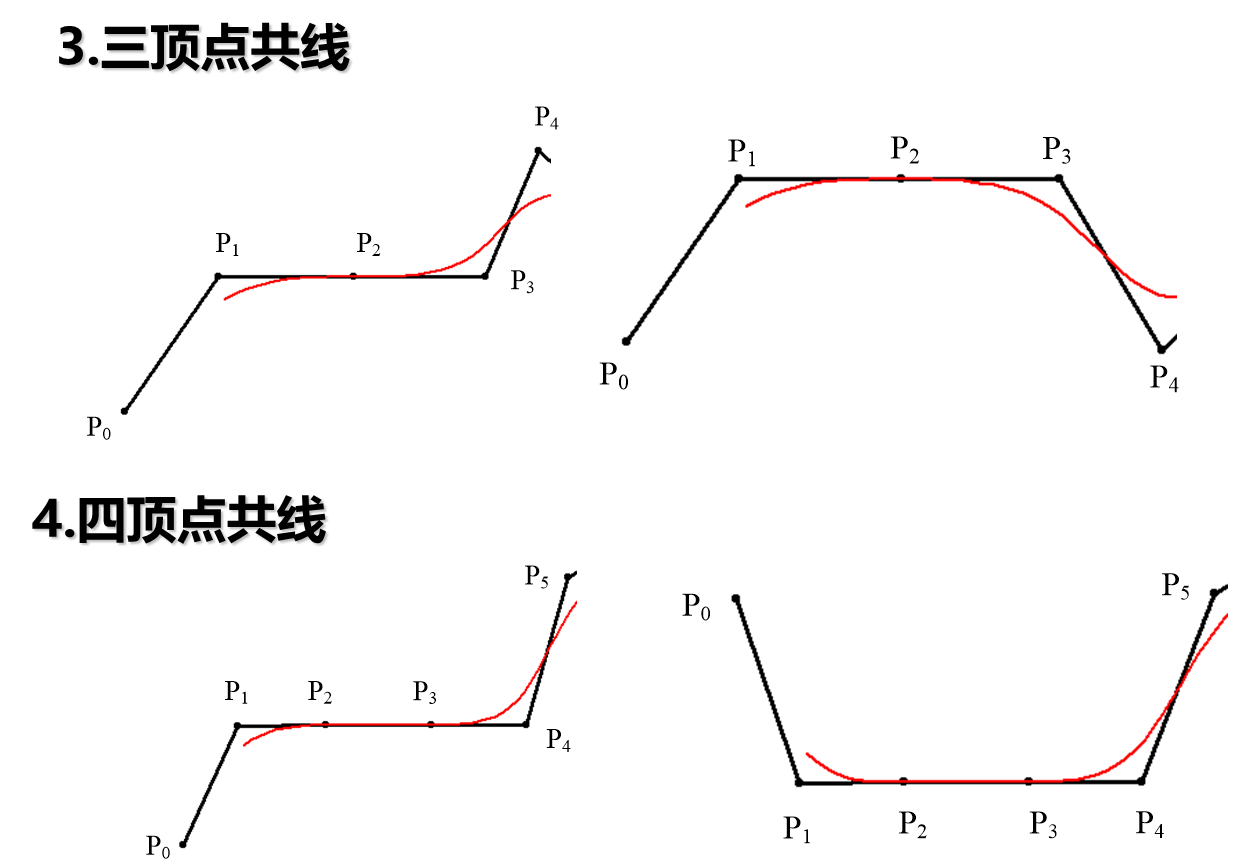
B样条曲面

定义

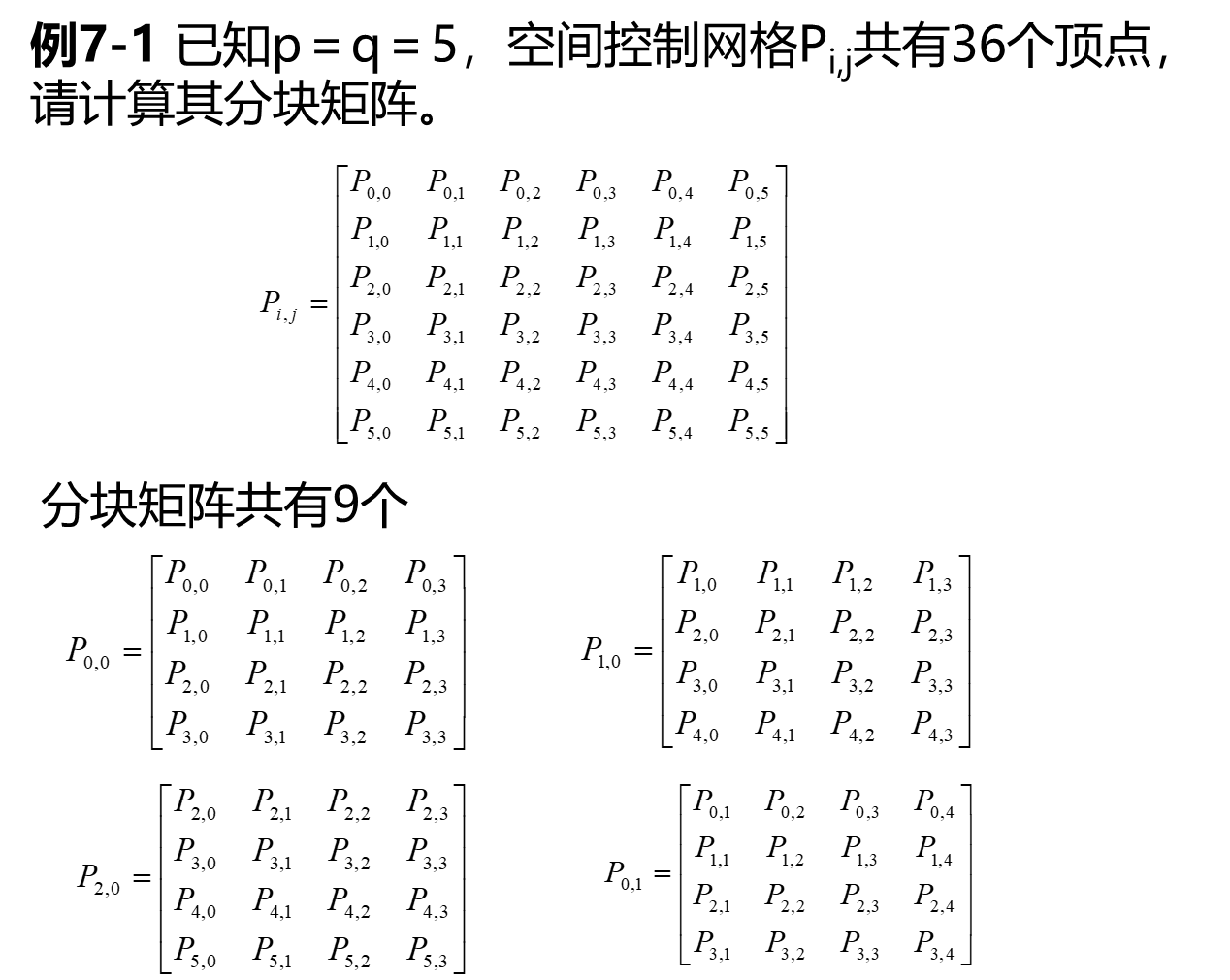
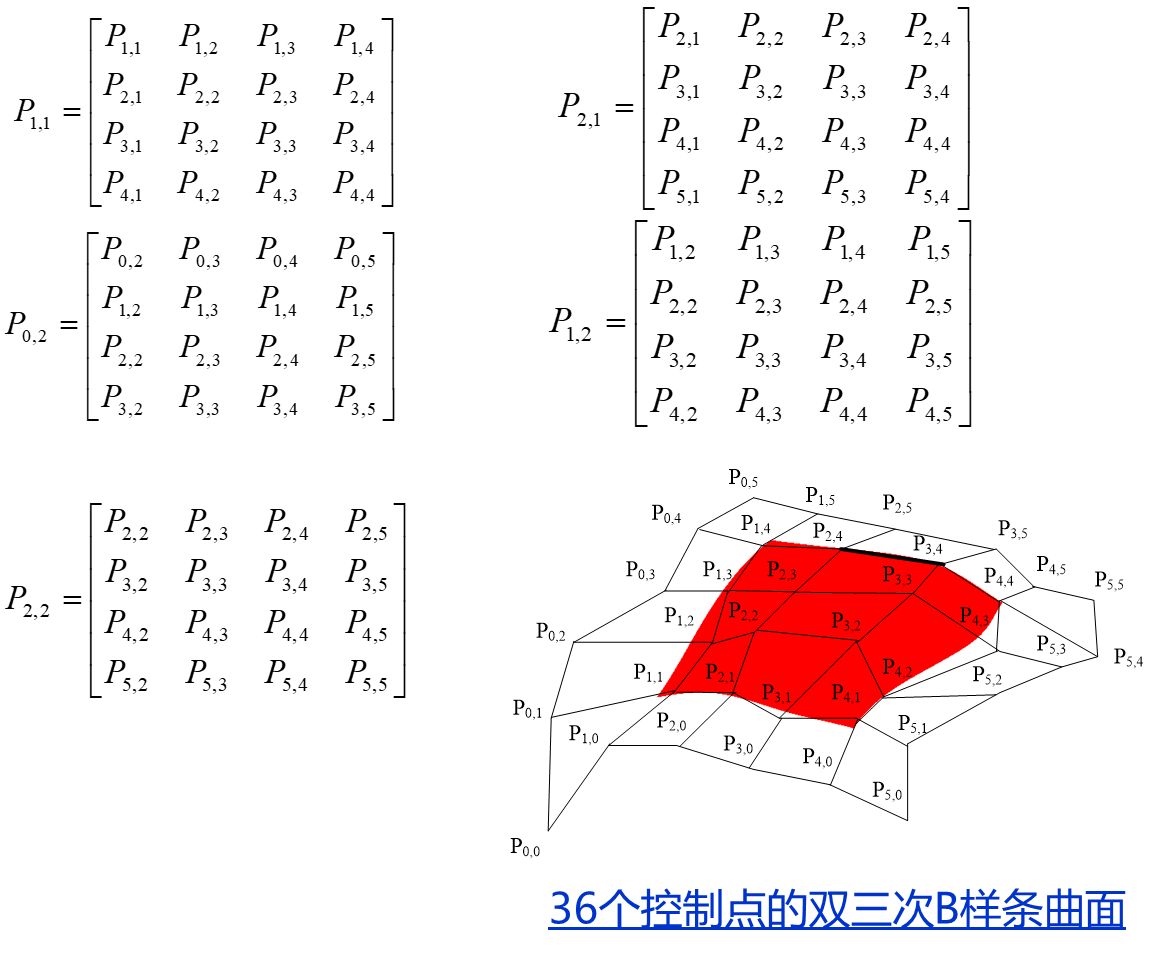
双三次B样条曲面的定义

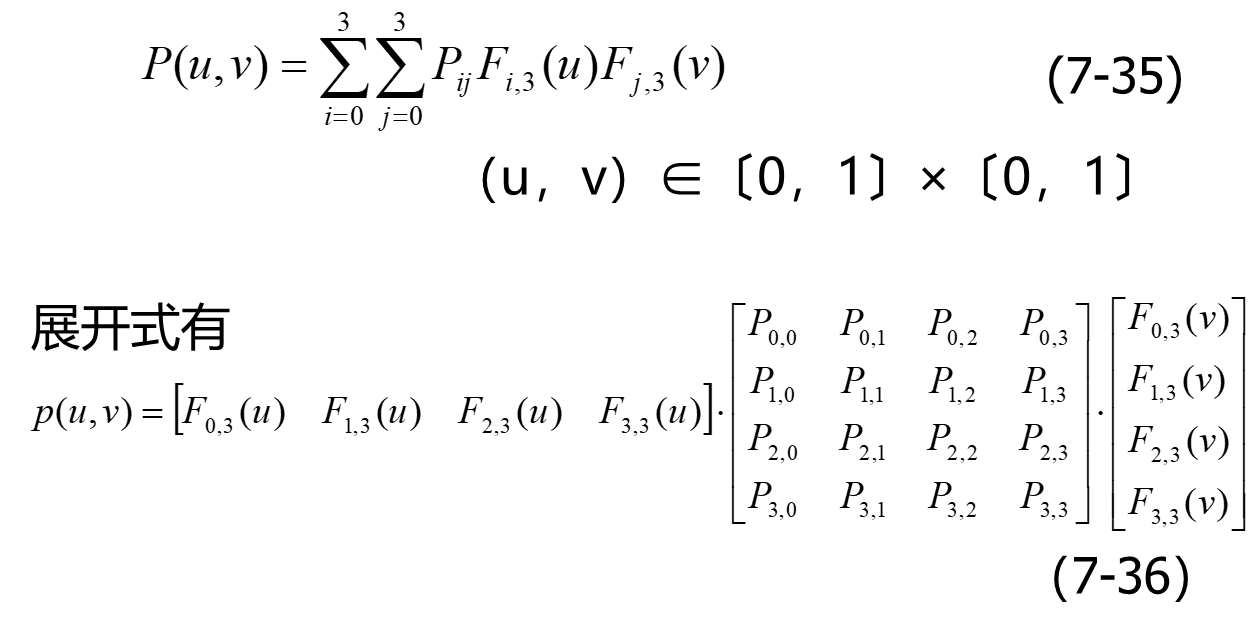
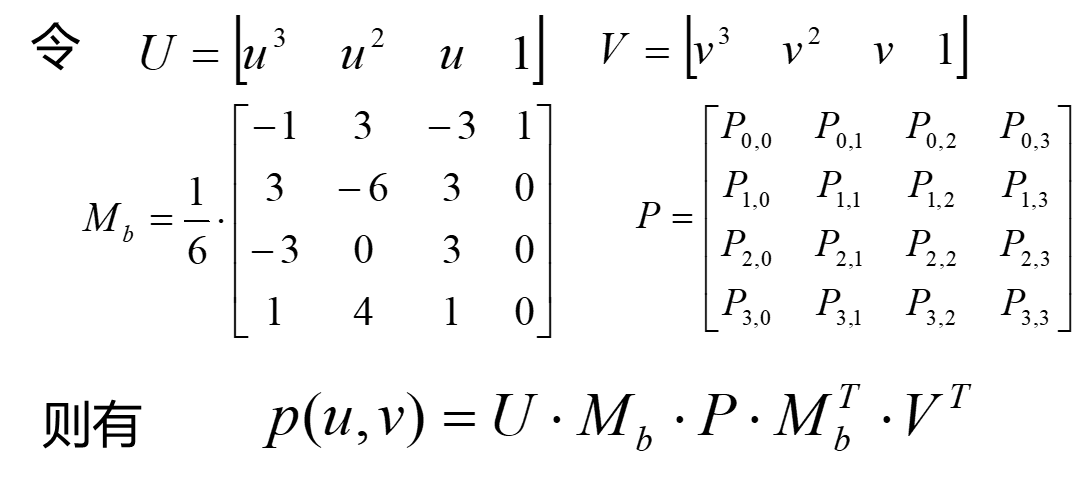
双三次B样条曲面是由三次B样条曲线交织而成。曲面生成时可以先固定u, 变化v得到一簇三次B样条曲线；然后固定v，变化u得到另一簇三次B样条曲线。与三次B样条曲线相似，双三次B样条曲面一般情况下不通过控制网格的任何顶点。

双三次B样条曲面的连续性

B样条曲线和Bezier曲线的最主要差别在于基函数不同。

Bernstein基函数是一个整体函数，而B样条基函数一个分段函数，所以B样条曲线可以进行局部控制点调整。

Bezier曲线曲面的阶次与控制多边形的顶点数有关，B样条曲线曲面的阶次可以自由决定。这样如果控制多边形顶点数超过4个时，两段三次Bezier曲线或两张双三次Bezier曲面片之间连接时就存在拼接的问题，而B样条曲线曲面可以自由地扩展到多个控制点，始终保持阶次不变，而且扩展后的分段曲线或分段曲面实现了自然连接。