参考内容

• 参考视频：不愧是王树森教授！6小时让我搞定了【深度强化学习完整版】我不信还有人学不明白！

• 强化学习基础

动作价值函数（Action-value Function）

• 这部分是对价值函数的回顾，在 强化学习基础 中进行了详细的讲解，看不懂这篇文章的先去简单翻一下
  

• $U_t$ 代表的是 discounted return，是从当前时刻 $t$ 到游戏结束得到的 reward 的折算总和，我们的目标是在游戏结束的时候，希望 $U_t$ 能够越大越好

• 而 $U_t$ 中的每个 $R_i$ 都取决于其所处的环境状态 $S_i$ 和采取的行为 $A_i$，因此 $U_t$ 直接与 $R_t,R_{t+1},...$ 相关，也就是直接与 $A_t,A_{t+1},...$ 以及 $S_t,S_{t+1},...$ 相关

• 强化学习过程中有两个部分会引入随机性：

  1. 是 agent 采取 action 的时候是根据 策略函数（分布） $\pi$ 进行随机抽样得到的
  2. 是 环境产生 state 的时候是根据 状态转移函数（分布） $p(s^{\prime },s,a)$ 随机抽样得到的

• 因为在每个 action 和 state 的产生过程中都会引入随机性，就导致了每个 $R_i$ 都是随机变量，而这也进而导致了 $U_t$ 是个随机变量

• $U_t$ 的值可以反映出从 $t$ 直到未来游戏结束的 reward 总和

• 而由于 $s_t,a_t$ 是在 $t$ 时刻可以观察到的，因此对于 $t$ 时刻往后的 $a_i$ 和 $s_i$ 我们通过 期望 的计算来消除随机性：$$Q_{\pi }(s_t,a_t)=\mathbb{E}[U_t|S_t=s_t,A_t=a_t]$$

• 因此 $Q_{\pi }(s_t,a_t)$ 只与 $\pi ,s_t,a_t$ 这三个部分有关：

  • $\pi$ 是当前 agent 采用的 策略，也可以看做是个概率分布
  • $s_t$ 是在 $t$ 时刻的环境状态
  • $a_t$ 是在 $t$ 时刻，agent 面对环境 $s_t$ 从策略 中随机抽样获得的 action

• 当然， $Q_{\pi }(s_t,a_t)$ 的值越大，代表在当前环境状态 $s_t$ 下，按照当前使用的 $\pi$ 策略 采样得到的 action $a_t$ 越正确。但 策略 有很多种，未必当前这种就是最好的，因此如果在所有可选的 策略 中得到一个使 $Q_{\pi }(s_t,a_t)$ 最大的值，即 $$Q^{\ast }(s_t,a_t)=\underset{\pi }{\max }{Q}_{\pi }(s_t,a_t)$$

• $Q^{\ast }(s_t,a_t)$ 终于摆脱了策略 $\pi$ 的影响，能够代表在当前环境状态 $s_t$ 的情况下，无论你采用何种 策略，采取 $a_t$ 在未来得到的最大的 action 收益的总和就是 $Q^{\ast }(s_t,a_t)$

• 然而 $a_t$ 可能取值的范围是 agent 的所有动作集合，例如马里奥游戏中的 up, right, left 这三种 action 构成了马里奥所有的动作。那么当在 $t$ 时刻马里奥面对环境 $s_t$ 时按照 $\pi$ 进行抽样得到了 $a_t\to up$，马里奥应该向上跳，此刻我们可以用 $Q^{\ast }$ 来评估出 向上跳 这个动作能够在未来获得的最大 return。

• 我们这里完全可以不采取 随机抽样 的方式得到 $a_t$ ，而是遍历所有的 $a_t$ 从而获得在当前 $t$ 时刻对于所有 $a_{t1},...a_{tn}$ 中能够获得最大 $Q^{\ast }$ 分数的 $a_t$ 作为当前 $t$ 时刻的 action，比如 $t$ 时刻：

  • up 行为的 $Q^{\ast }(s_t,up)=5000$
  • right 行为的 $Q^{\ast }(s_t,right)=3000$
  • left 行为的 $Q^{\ast }(s_t,left)=1000$

• 那么毫无疑问，我们应该让 agent 选择 up 作为 $t$ 时刻的 action

深度强化学习（DQN）

学习目标（Goal）

• 在游戏结束时获得的总收益 total reward 越大越好
• 在上个部分我们已经说明了如何用 $Q^{\ast }$ 描述 agent 在$t$ 时刻面对环境 $s_t$ 时采取agent 所有可能的action从而选取最大的 $Q^{\ast }$ 值，这个过程我们描述成：$$a^{\ast }=\underset{a}{\mathrm{argmax}}{Q}^{\ast }(s_t,a)$$
• $a^{\ast }$ 是在 $t$ 时刻面对 $s_t$ 能够选取的最好的 action
• 下面对几点进行重点的说明：

  • $Q^{\ast }$ 虽然能够帮我们在 $t$ 时刻确定最好的行为 $a^{\ast }$，但得出这个结论并不代表着这个 $a^{\ast }$ 完全就是最好选择，而是 期望，证明 $a^{\ast }$ 这种行为从概率的角度来看是最好的选择，但未来啥样谁也不能精确描述

  • 基于 动作价值函数 的强化学习求解思路就是帮我们用神经网络模拟一个强大的 $Q^{\ast }$ 函数，从而在每个时刻 $i$ 帮我们决定采取最好的 $a^{\ast }$ 作为 action

  • 如果我们想象现实的情况，这似乎不可能，因为 $Q^{\ast }$ 函数好像一个先知，它是怎么知道某个 action 在未来的 期望 的？这就好像是一个人告诉你说：“小伙子，你可以选下面三只股票，虽然我不能告诉你他们的具体交易细节，但是我可以告诉你的是，在游戏结束的时候，$a_1$ 股票会翻 $10$ 倍，$a_2$ 翻 $3$ 倍，而 $a_3$ 亏钱”

  • 但其实这在一些特定的环境（游戏环境）中是有可能的。比如你把自己看做一个 $Q^{\ast }$ 当你玩一个特定的游戏 $100000$ 局的时候，你其实就变成了先知，因为对于过去大量的数据，你已经知道因果了，而且你玩的局数越多，对于因果的对应关系和发展规律就捕捉的越全面，所以此时如果你指导一个 agent，他觉得你未卜先知，其实只是你通过大量的数据推算了大致的情况。而且你给他提供的建议也并不完全是真正的 期望，而是你根据你自己的已知情况推出的近似真实 期望 的结果。

  • 更通俗讲：

    • 你看似是先知，其实是看了大量的数据，你可以通过大量的数据无限逼近真实的先知，但你永远是个假的先知
    • 你可以根据看过的数据来推算 agent 在当前状态下采取所有行为的 期望（并非真实的 期望，而是你基于过去数据而计算的 期望）
    • agent 根据你提供的 期望 作为参考，选择一个当前时刻最好的行为

  • 深度神经网络就是在扮演这个 伪装的先知 的角色。通过大量的数据训练，神经网络似乎在某个时刻 $t$ 能够帮 agent 判断每个动作在未来的 期望收益，如果神经网络足够好，那么 期望 的结果就足够准确，agent 就能够足够好。

如何获得尽可能好的 $Q^{\ast }(s_t,a)\to$ 用神经网络通过学习获得

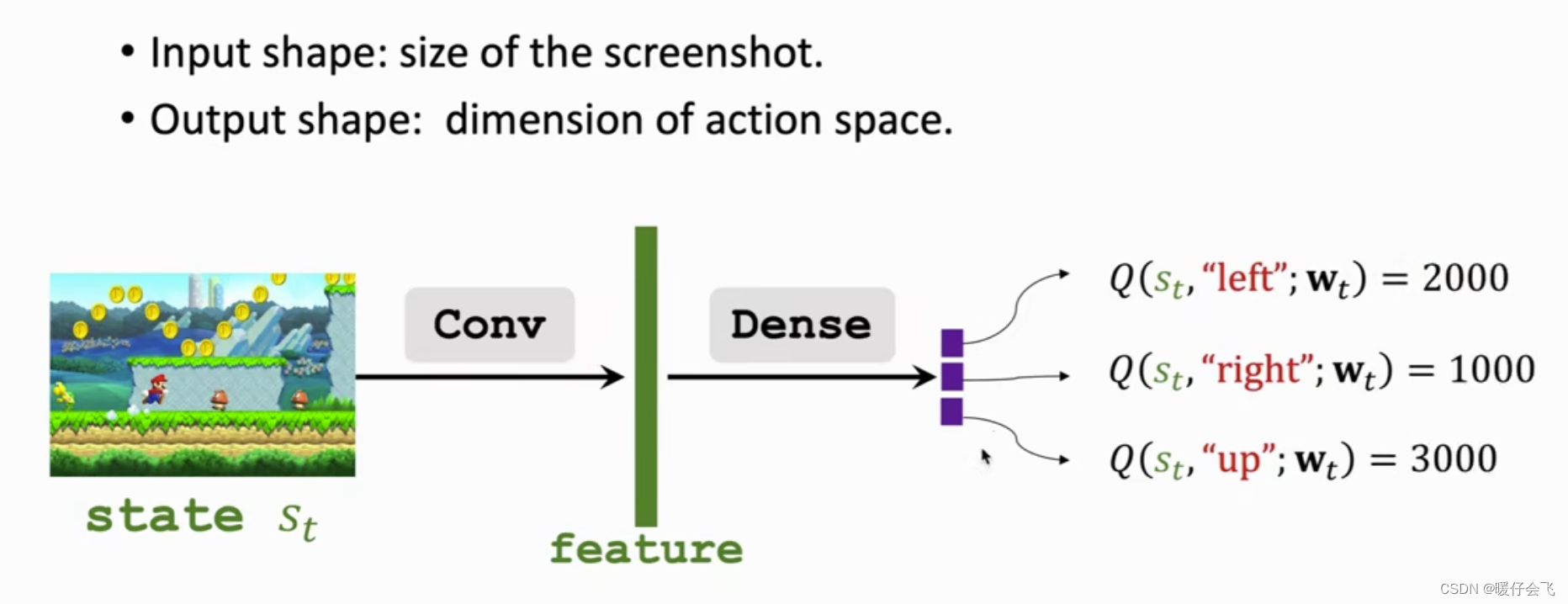
• 用 $Q(s_t,a;w)$ 表示神经网络，我们的目标是近似真实情况的 $Q^{\ast }(s_t,a)$
  

• 我们构造一个神经网络，将 state 作为输入，输出是神经网络对于每个 action 的打分，在这个例子中：

  • left 得分为 2000
  • right 得分为 1000
  • up 得分为 3000

• 那么我们认为马里奥应该采取 up 作为 action

• 重复这个过程，流程图如下：
  

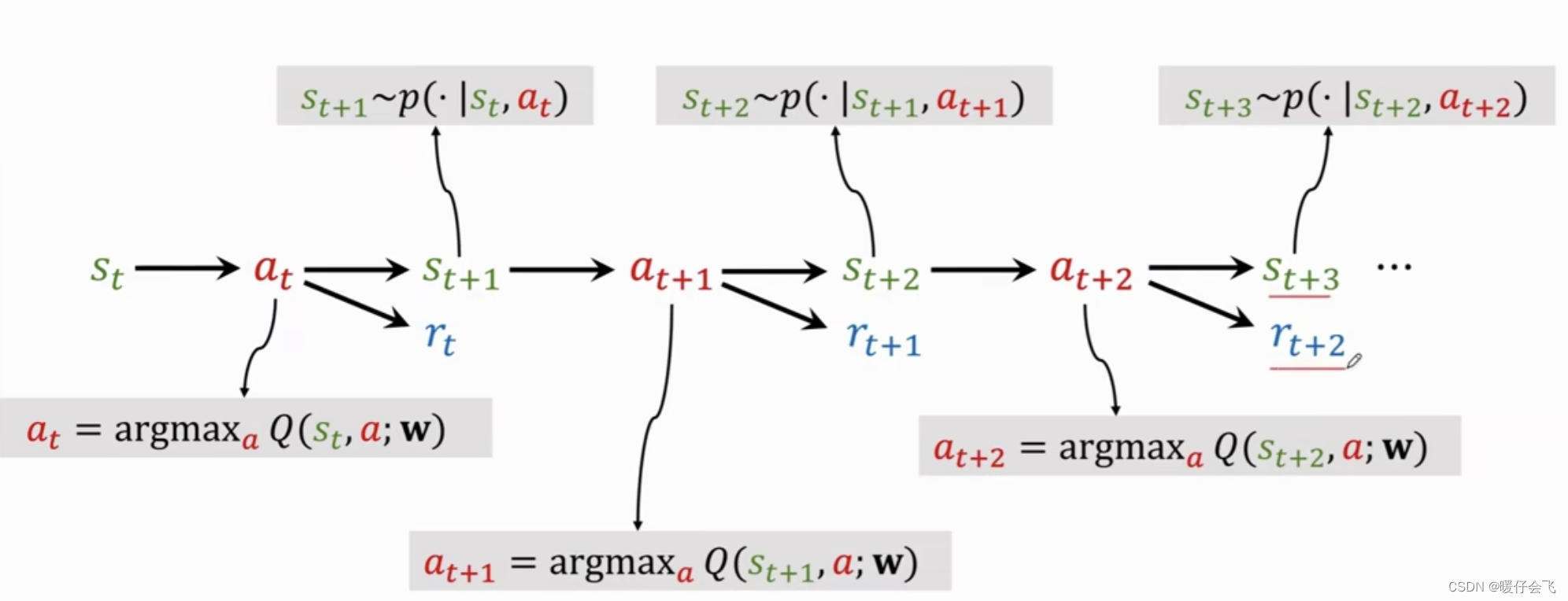
  • $t$ 时刻根据神经网路的结果选择出 $a_t$ 然后环境状态更新为 $s_{t+1}$ 的同时给出 $a_t$ 的奖励 $r_t$
  • 神经网络根据 $r_t,r_{t+1},...$ 进行训练，得到更好的对动作的评估结果一直到游戏结束

时间差分算法（Temporal Difference, TD）算法

• 我们要训练一个好的神经网络来模拟 $Q^{\ast }(s_t,a)$ 要用 TD 算法来完成训练
• 文章下面的思路是：
  • 讲述 TD 算法的核心思想
  • 将 TD 算法的核心思想应用到强化学习的神经网络训练中，从而获得更好的 $Q^{\ast }(s_t,a)$ 函数近似

TD 算法的核心思想

• NYC, Atlanta, DC 都是地名
• 现在有一个时间评估器 $Q(w)$， 它的参数是 $w$，开始它很不准确，但现在我们想训练 $Q(w)$ 使得它能够给出某地到另一地的路程花费时间精确值。所以训练目标是得到一个更好的 $Q(w)$
• 为了训练 $Q(w)$ 我们需要在现实世界中通过多次开车的实际测量值来修正 $Q(w)$ 做出的预测结果，这样 $Q(w)$ 的预测才会越来越准确

---

• 用一组实际的数值来更详细地描述这个过程：
  
  • 我要驱车从 NYC 去 Atlanta 假设现在 $Q(w)$ 没有进行任何的训练，那么它给出了一个近似瞎猜的评估结果 $q=1000$，即，$Q(w)$ 认为 NYC 去 Atlanta 要花费 $1000min$
  • 但是当我真正开车从 NYC 去 Atlanta 发现真实的距离 $y=860km$
  • 所以我们定义损失函数 $L=\frac{1}{2}(q-y{)}^2$ （你可以按照自己的喜好定义损失，这里就用最简单的平方差损失），根据损失函数，我们可以得到这趟旅程 $Q(w)$ 的损失值的具体数值是 $140^2$
  • 然后采用神经网络优化常用的梯度下降算法来更新 $Q(w)$ 中的权重参数 $w$，这样当我下一次用 $Q(w)$ 的时候，它就能够给出比现在更好的结果了。
  • 当我重复这个过程非常多的次数，$Q(w)$ 就会被训练的越来越好
  • 但现在同样面对一个问题：我只要想更新 $Q(w)$ 就必须完成一整趟旅程，这代价也太大了。有没有一种方式能够利用部分的信息来更新参数，从而不浪费任何一点机会呢？
  • 这就是 TD 算法的核心思想了

---

• 从 NYC 开车去 Atlanta 时车抛锚在了 DC，然后修了三天车从 DC 折返回 NYC
• 假设 $Q(w)$ 只能给出从 NYC 到 Atlanta 的预测值 $q_{na}$ 以及从 DC 到 Atalanta 的预测值 $q_{da}$ 那么这时候 TD 算法 是如下更新参数的：
  

  • 首先开车开到 DC 的时候一看路程，发现走了 $300min$ 这是真实的观测值

  • 现在模型给出从 DC 到 Atlanta 要花费的预估时间 是 $600min$，所以结合 真实的 $300min$ 和第二次预测的值 $600min$ 我们将从 NYC 到 Atlanta 的整体预估结果更新成 $900min$，这个 $900min$ 就是 TD-target 虽然这个值也是个估测值，但是比开始的 $1000min$ 更加可靠

  • 当你越接近 Atlanta 通过 TD-target 的方式获得的值就估计的越准

  • 现在我们的形式化以上的过程：

    • $q=1000$，但是 $y_{td}=900$
    • 因此这时候如果依然采用 均方误差 计算 $L$，那么损失值是 $L=(q-y_{td}{)}^2=100^2$，可以看到通过这种方式我们并不需要真正到达目的地，通过 部分真实值 + 部分预估值 的方式也能够不断地更新 $Q(w)$ 的参数

TD 算法在 DQN 中的应用

• 使用 TD 算法的条件是：$$T_{NYC\to ATL}\approx T_{NYC\to DC}+T_{DC\to ATL}$$
  • 其中 $T_{NYC\to ATL},T_{DC\to ATL}$ 是通过同一个模型 $Q(w)$ 估计值，而 $T_{NYC\to DC}$ 是真实的能够确定的值
    
• 在 DQN 中，我们知道在 $t$ 时刻的奖励 $r_t$ 是环境在 $t+1$ 时刻给出的，因此我们确切地可以知道 $r_t$ 的值，因此我们构建公式：$$Q(s_t,a_t;w)\approx r_t+\gamma Q(s_{t+1},a_{t+1};w)$$
  • $Q(s_t,a_t;w)$ 表示从 $t$ 时刻往后直到游戏结束时的 return 的期望值，这个值越大代表当前的 $a_t$ 越合理
  • $Q(s_{t+1},a_{t+1};w)$ 代表从 $t+1$ 时刻往后直到游戏结束时的 return 的期望值，这个值越大代表 $t+1$ 时刻采取的 $a_{t+1}$ 越好
  • 那么这个公式是怎么得到的呢？

$Q(s_t,a_t;w)\approx r_t+\gamma Q(s_{t+1},a_{t+1};w)$ 公式来源

• 之前我们推导过：$$U_t=R_t+\gamma R_{t+1}+{\gamma }^2{R}_{t+2}+....$$
• 简单地加个括号：$$U_t=R_t+\gamma (R_{t+1}+\gamma R_{t+2}+....)=R_t+\gamma (U_{t+1})$$，即：$$U_t=R_t+\gamma U_{t+1}$$
• 又因为我们知道 $$Q_{\pi }(s_t,a_t)=\mathbb{E}[U_t|s_t,a_t]\Rightarrow \underset{\pi }{\max }{Q}_{\pi }(s_t,a_t)=Q^{\ast }(s_t,a_t)$$，而我们通过神经网络模拟的是 $$\begin{gathered} a_t=\underset{a}{\mathrm{argmax}}{Q}^{\ast }(s_t,a); \\ Q(s_t,a_t;w)=Q^{\ast }(s_t,a_t) \end{gathered}$$，神经网络的输出结果可以看成是对 $U_t$ 期望 的一个估计值（因为我们只能近似 $U_t$ 的期望而不可能得到真实的 $U_t$ 的期望）
• 所以我们可以如下表示：$$Q(s_t,a_t;w)\approx \mathbb{E}[U_t]$$，同样的：$$Q(s_{t+1},a_{t+1};w)\approx \mathbb{E}[U_{t+1}]$$
• 所以我们可以进一步得到：$$Q(s_t,a_t;w)\approx \mathbb{E}[r_t+\gamma Q(S_{t+1},A_{t+1};w)]$$

利用 TD 算法更新神经网络模型

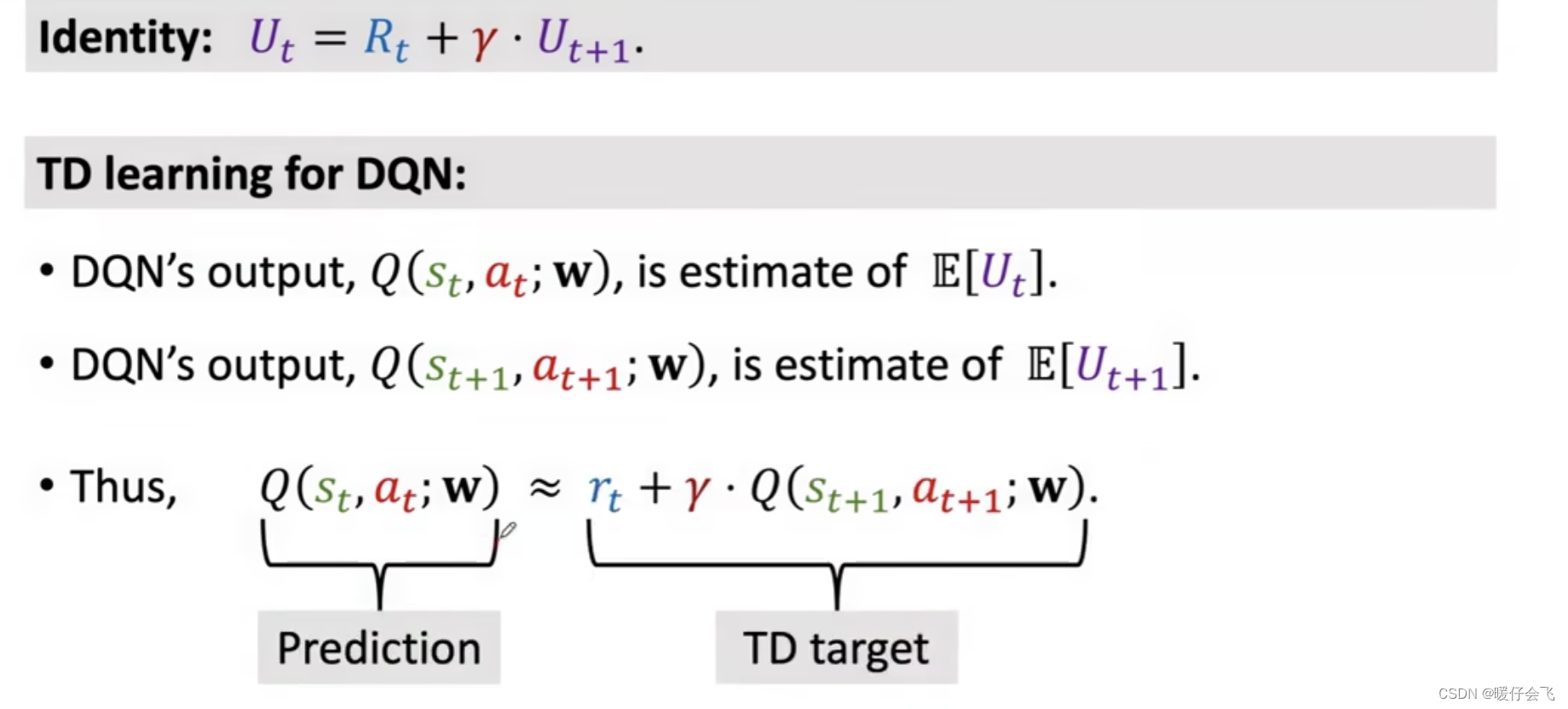
• 根据以上结果我们知道，在 $t$ 时刻：
  • 通过神经网络得到 $q=Q(s_t,a_t;w_t)$
  • 同时 TD target 的结果： $$\begin{gathered} y_{td}=r_t+Q(s_{t+1},a_{t+1};w_t), \\ {a}_{t+1}=\underset{a}{\mathrm{argmax}}Q(s_{t+1},a;w_t) \end{gathered}$$
  • 所以利用 $q$ 和 $y_{td}$ 可以求算 $L=\frac{1}{2}[q-y_{td}{]}^2$
  • 并采用梯度下降来更新神经网络
    

Value-Based 强化学习总结

• 最优价值函数定义：$$Q^{\ast }(s_t,a_t)=\underset{\pi }{\max }\mathbb{E}[U_t|S_t=s_t,A_t=a_t]$$， 其中

  • $a_t$ 最初是从 $\pi$ 中随机采样出来的
  • $s_t$ 是从状态转移函数 $p(s^{\prime },s,a)$ 中随机采样出来的
  • 当确定了 $a_t,s_t$ 之后就可以挑选出当前情况下最大的 $Q$ 值 $Q^{\ast }(s_t,a_t)$
  • 得到了 $Q^{\ast }(s_t,a_t)$ 这个函数之后，我们就可以对所有的 $a_t$ 进行打分（虽然之前的 $a_t$ 是随机采样出来的，但现在不同了，我们已经得到了 $Q^{\ast }$函数，我们要遍历 $t$ 时刻所有的行为从而获得最优的 $a_t$）

• 基于价值的强化学习最终目标就是学习一个神经网络来近似 $Q^{\ast }(s,a)$ 函数：

  • 输入是环境的某个状态 $s$
  • 输出是当前每个可选行为的分数

• 使用 TD 算法训练神经网络：