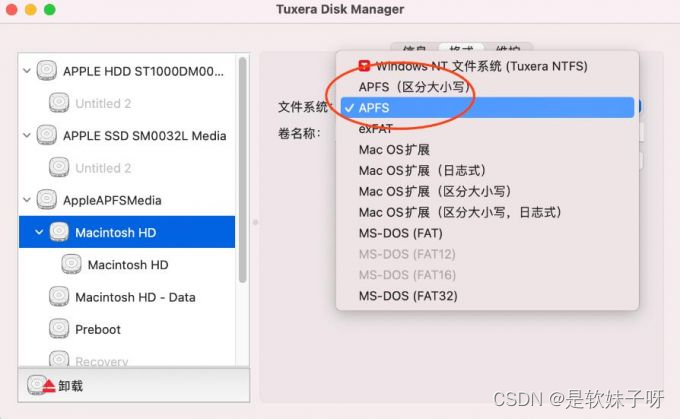
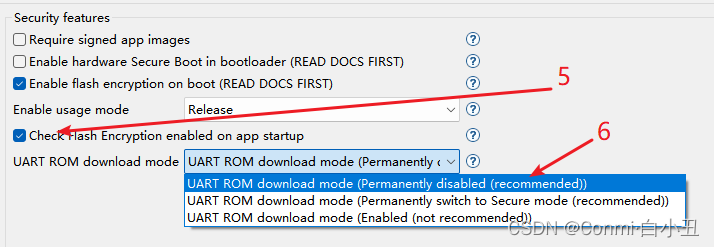
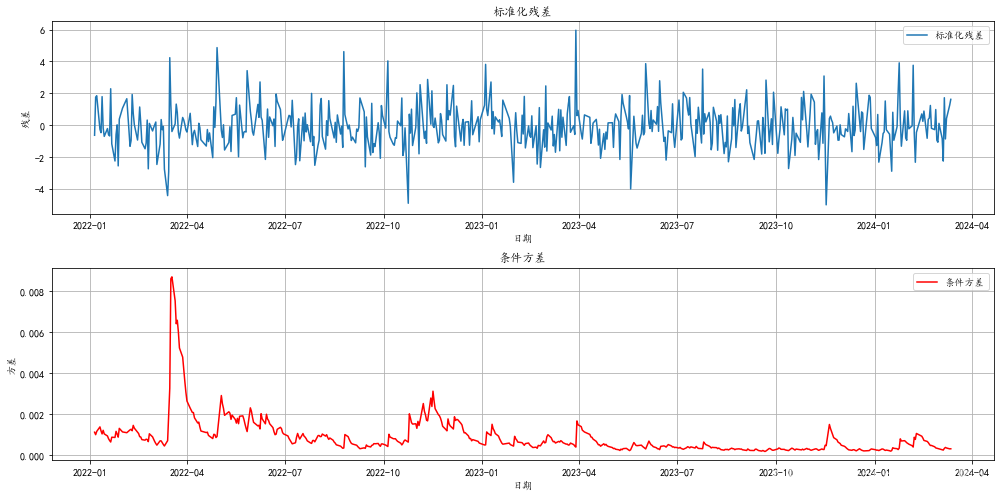
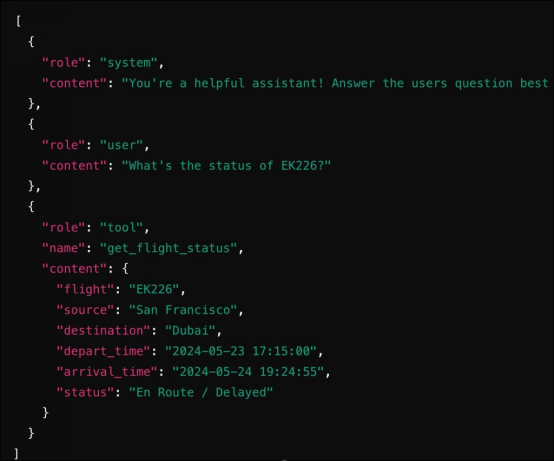
• 博客主页：音符犹如代码
• 系列专栏：算法练习
• 关注博主，后期持续更新系列文章
• 如果有错误感谢请大家批评指出，及时修改
• 感谢大家点赞👍收藏⭐评论✍

 

 

目录

思路

解题方法

时间复杂度

空间复杂度

Code 

---

思路

首先要解决如何获取一个整数各个数位上的数字之和。这可以通过不断对数字进行取余和整除操作来逐位获取数字，并累加求和。

然后，判断这个整数是否能被求得的数字之和整除。如果能整除，就返回数字之和；不能整除，就返回 -1 。

整体来说，思路就是先分解数字求其各位数字之和，再进行整除判断得出结果。

解题方法 

首先，通过一个循环计算输入数字 x 各个数位上的数字之和，并将其存储在变量 sum 中。然后，判断 x 是否能被 sum 整除，如果能整除则返回 sum，否则返回 -1。

时间复杂度

计算数字之和的循环执行的次数取决于数字 x 的位数，设数字 x 有 n 位，那么时间复杂度为 O(n)。

空间复杂度

只使用了固定的几个整型变量来存储中间结果和最终结果，空间复杂度为 O(1)。

Code

class Solution {
    public int sumOfTheDigitsOfHarshadNumber(int x) {
        int sum = 0;
        int num = x;

        while (num > 0) {
            sum += num % 10;
            num /= 10;
        }

        if (x % sum == 0) {
            return sum;
        } else {
            return -1;
        }
    }
}

"过去都是幻觉。而未来还有可期"——《了不起的盖茨比》弗朗西斯·斯科特·菲茨杰拉德