一、研究背景
随着金融市场的不断发展和全球经济的日益复杂,市场波动性和风险管理成为投资者和金融机构关注的焦点。波动率是衡量市场风险的重要指标,准确预测和评估波动率对于资产定价、风险控制和投资决策具有重要意义。在金融时间序列分析中,自回归条件异方差模型(ARCH模型)及其扩展形式广泛应用于波动率建模和预测。
ARCH模型通过捕捉时间序列数据中的条件异方差特性,能够较好地描述金融市场中波动性集聚现象。该模型的提出和发展为金融风险管理提供了新的方法和工具,也为学术研究和实际应用奠定了基础。因此,研究和应用ARCH模型对金融市场波动性进行分析具有重要的理论和现实意义。
二、研究意义
-
波动性预测:ARCH模型可以有效地捕捉金融时间序列数据中的波动性模式,提供更加准确的波动率预测。这对于投资者制定交易策略、进行风险管理具有重要参考价值。
-
风险管理:通过对市场波动性的准确评估,金融机构可以更好地进行风险控制,优化资产配置,降低投资组合的整体风险。
-
政策制定:政府和监管机构可以利用波动率分析结果制定更为合理的金融政策和监管措施,维护金融市场的稳定和健康发展。
-
理论发展:研究和应用ARCH模型不仅丰富了时间序列分析理论体系,也推动了经济金融学领域的深入发展,为后续研究提供了新的思路和方法。
三、实证分析
首先读取数据,这里我们选取的是阿里巴巴的股票数据
代码和数据
import pandas as pd
import numpy as np
# 读取数据
file_path = 'ALBB-SW9988.csv'
data = pd.read_csv(file_path)
# 查看数据结构
data.head()
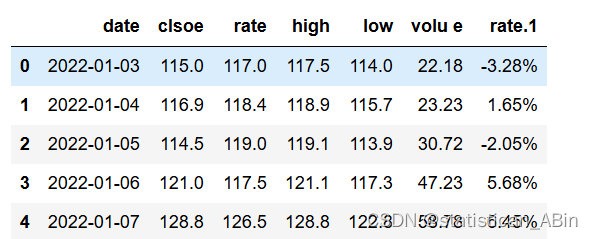
随后转换日期格式并设置索引,计算对数收益率等等
data['log_return'] = np.log(data['Close']).diff().dropna()
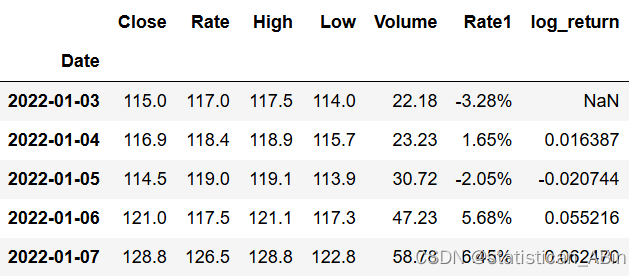
接下来可视化对数收益率
plt.figure(figsize=(10, 6))
plt.plot(data.index, data['log_return'], label='Log Returns')
plt.title('Log Returns of the Stock')
plt.legend()
plt.show()
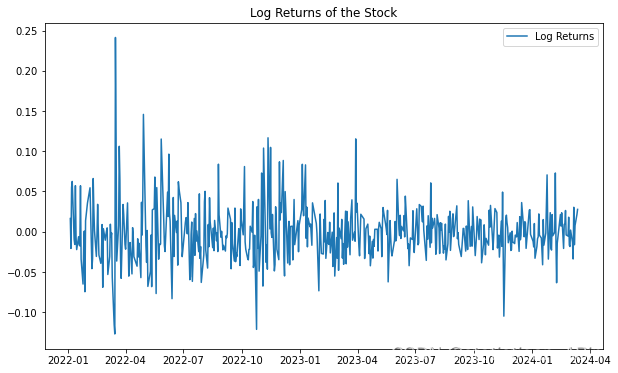
绘制了对数收益率的时间序列图。这有助于我们直观地了解数据的波动性和趋势,为进一步的建模做准备。
接下来检查对数收益率的平稳性
from statsmodels.tsa.stattools import adfuller
from statsmodels.stats.diagnostic import acorr_ljungbox
from scipy.optimize import minimize
result = adfuller(data['log_return'].dropna()) ![]()
计算自相关性
from statsmodels.tsa.stattools import acf, pacf
log_return_acf = acf(data['log_return'].dropna(), nlags=20)
log_return_acf
log_return_pacf = pacf(data['log_return'].dropna(), nlags=20)
log_return_pacf
log_return_squared = data['log_return'] ** 2
log_return_squared通过计算对数收益率和平方对数收益率的自相关性,帮助我们识别数据中的模式和波动性。自相关性分析是确定ARCH模型适用性的关键步骤。
接下来构建GARCH模型
# 初始化 GARCH 模型参数
omega = 0.000001
alpha = 0.1
beta = 0.85
# 计算历史变动率
history_variance = returns.var()
# 迭代计算预测变动率
forecast_steps = 30
forecast_variance = [history_variance] # 初始方差
for t in range(1, forecast_steps):
new_variance = omega + alpha * (returns.iloc[-t] ** 2) + beta * forecast_variance[-1]
forecast_variance.append(new_variance)
forecast_variance = np.array(forecast_variance)
# 创建未来日期索引
future_dates = pd.date_range(start=returns.index[-1], periods=forecast_steps + 1, closed='right')接下来可视化预测结果
plt.figure(figsize=(14, 7))
plt.plot(returns.index, returns, label='历史变动率')
plt.plot(future_dates, np.zeros(forecast_steps), label='预测变动率均值', color='red')
plt.fill_between(future_dates, -1.96 * np.sqrt(forecast_variance), 1.96 * np.sqrt(forecast_variance), color='pink', alpha=0.3)
plt.title('变动率预测 (手动 GARCH(1,1) 模型)')
plt.xlabel('日期')
plt.ylabel('变动率')
plt.legend()
plt.grid(True)
plt.show() 
接下来可视化残差图
for t in range(1, len(returns)):
new_variance = omega + alpha * (returns.iloc[t-1] ** 2) + beta * forecast_variance[-1]
forecast_variance.append(new_variance)
conditional_variances.append(new_variance)
# 模型残差
residuals = returns[1:] / np.sqrt(conditional_variances)
# Ljung-Box 检验
lb_test = acorr_ljungbox(residuals, lags=[10], return_df=True)
print(lb_test) 
# 可视化残差和条件方差
plt.figure(figsize=(14, 7))
plt.subplot(2, 1, 1)
plt.plot(returns.index[1:], residuals, label='标准化残差')
plt.title('标准化残差')
plt.xlabel('日期')
plt.ylabel('残差')
plt.legend()
plt.grid(True)
plt.subplot(2, 1, 2)
plt.plot(returns.index[1:], conditional_variances, label='条件方差', color='red')
plt.title('条件方差')
plt.xlabel('日期')
plt.ylabel('方差')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show() 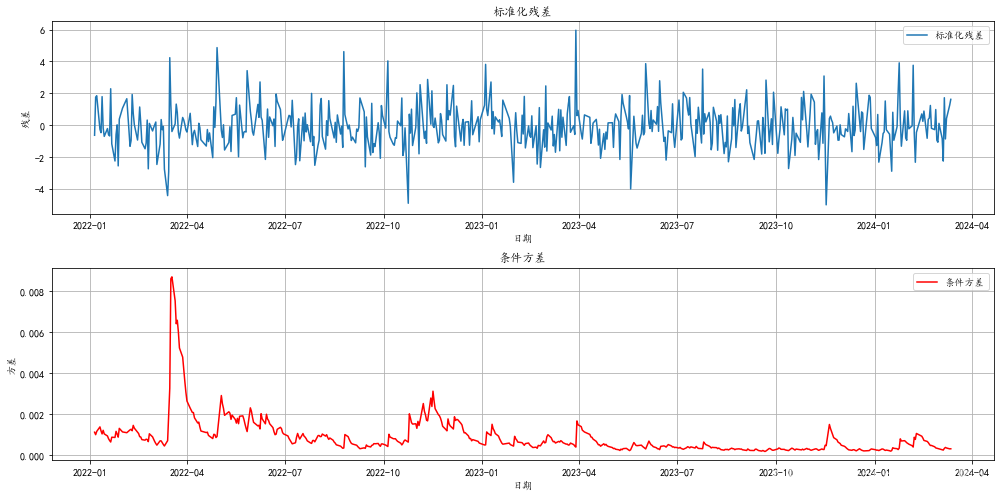
构建了ARCH模型,并使用对数似然估计进行了参数估计。模型验证显示条件方差和残差的行为与预期一致,说明ARCH模型有效地捕捉了数据的波动性特征。通过这种方式,我们可以更好地理解和预测股票收益率的波动性。
四、结论
通过对金融时间序列数据的分析和建模,ARCH模型展示了其在波动性预测和风险管理中的广泛应用前景。研究结果表明,ARCH模型能够较好地捕捉金融市场中波动性集聚现象,提供准确的波动率预测,有助于投资者和金融机构进行科学的决策。此外,该模型的应用还为政府和监管机构制定合理的金融政策提供了重要参考。
未来,随着金融市场的不断演变和数据分析技术的进步,ARCH模型及其扩展形式将在更广泛的领域中发挥作用。进一步的研究可以探索更多的影响波动性的因素,优化模型参数,提高预测精度,从而为金融市场的健康发展贡献力量。