PPT 截取有用信息。 课程网站做习题。总体 MOOC 过一遍
- 1、学堂在线 视频 + 习题
- 2、相应章节 过电子书 复习 【下载: 本章 PDF GitHub 页面链接】
- 3、 MOOC 习题
- 跳过的 PDF 内容
学堂在线 课程页面链接
中国大学MOOC 课程页面链接
B 站 视频链接
PPT和书籍下载网址: 【GitHub链接】
文章目录
- 8.1 值表示: 表格 ——> 函数
- 8.2 状态值 估计
- 8.4 Deep Q-leaning 【DQN】

第 7 章: 基于表格的 TD 学习算法
本章: 基于函数的 TD 学习算法
神经网络
DQN

8.1 值表示: 表格 ——> 函数

表格:直接重写表中相应的条目
函数:通过更新
w
w
w 间接地更改值
优点: 直观,便于分析。
缺点: 难以处理 大的 或 连续的 状态或动作
两个方面:1) 存储; 2) 泛化能力。
有很多的 状态-动作 对, 不可能都访问到。
曲线近似, 节省存储空间。
- 无法精确表示 状态值。
函数近似法通过牺牲精度来提高存储效率。
idea: 使用参数化函数 v ^ ( s , w ) ≈ v π ( s ) \hat v(s, w)\approx v_\pi(s) v^(s,w)≈vπ(s) 近似 状态和动作值,其中 w ∈ R m w \in \mathbb R^m w∈Rm 是参数向量。
优点:
1) 存储
w
w
w 的维数可能比
∣
S
∣
|\mathcal S|
∣S∣小得多。
2) 泛化:
当一个状态
s
s
s 被访问时,参数
w
w
w 被更新,这样其他一些未访问状态的值也可以被更新。通过这种方式,学习值 可以推广到 未访问状态。
8.2 状态值 估计
P2
真实状态值 v π ( s ) v_\pi(s)~~~ vπ(s) 估计值 v ^ ( s , w ) \hat v(s, w) v^(s,w)
为了找到最优的
w
w
w,我们需要两个步骤:
1、定义一个目标函数。
2、推导 优化目标函数 的算法。
目标函数: J ( w ) = E [ ( v π ( S ) − v ^ ( S , w ) ) 2 ] J(w) =\mathbb E[(v_\pi(S)-\hat v(S, w))^2] J(w)=E[(vπ(S)−v^(S,w))2]
误差 的平方。
——————
期望是 关于 随机变量
S
∈
S
S\in \mathcal S
S∈S 的, 那么
S
S
S 的概率分布是什么?
平均分布。 每个 状态的 权重都是 1 ∣ S ∣ \frac{1}{|\mathcal S|} ∣S∣1
J ( w ) = E [ ( v π ( S ) − v ^ ( S , w ) ) 2 ] = 1 ∣ S ∣ ∑ s ∈ S ( v π ( s ) − v ^ ( s , w ) ) 2 J(w) =\mathbb E[(v_\pi(S)-\hat v(S, w))^2]=\frac{1}{|\mathcal S|}\sum\limits_{s\in\mathcal S}(v_\pi(s)-\hat v(s, w))^2 J(w)=E[(vπ(S)−v^(S,w))2]=∣S∣1s∈S∑(vπ(s)−v^(s,w))2
给重要的状态 更大的权重。
平稳分布:稳态分布, 极限分布
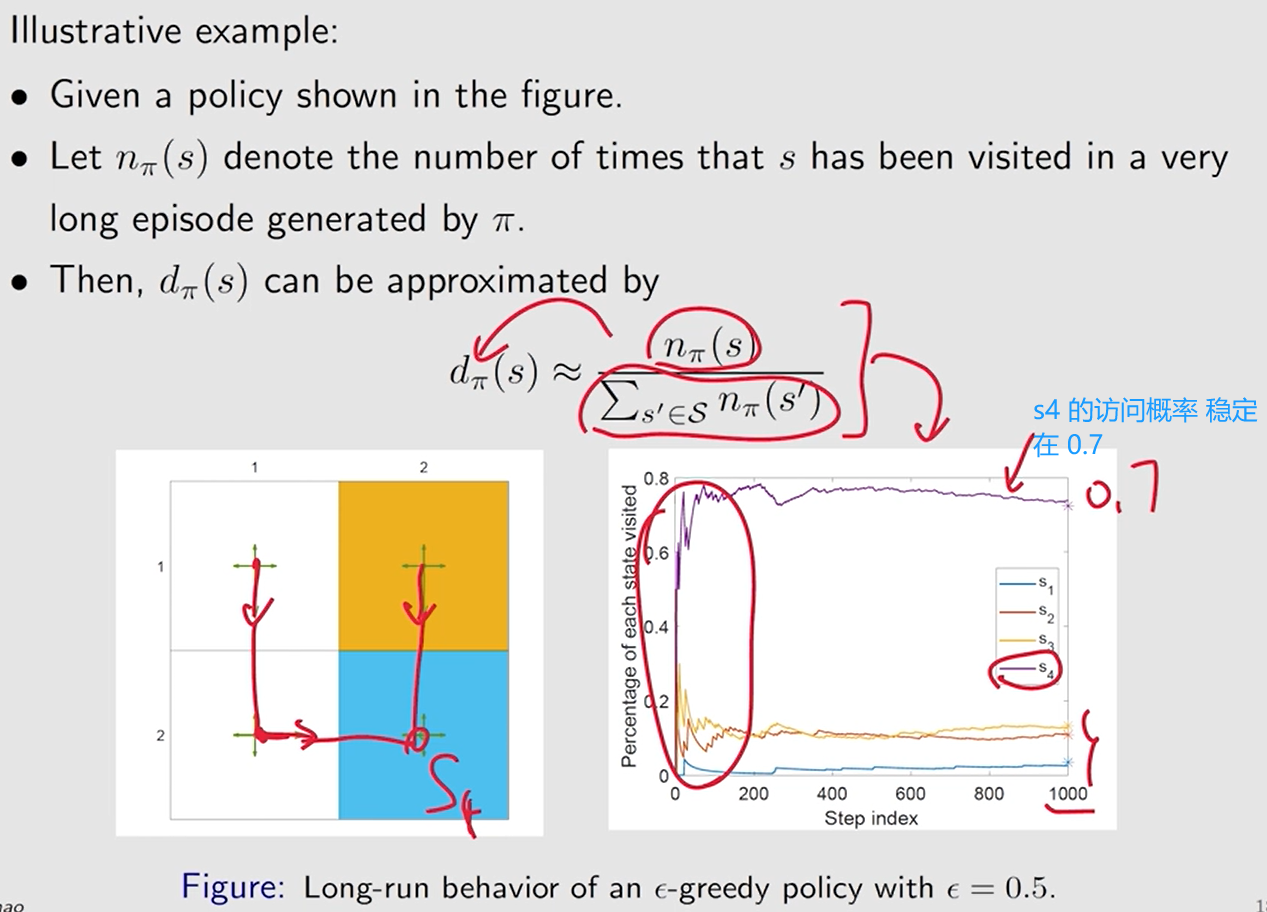
马尔可夫过程 的长期行为
在代理执行给定策略足够长的时间后,代理处于任何状态的概率可以用这个平稳分布来描述。
基于策略 π \pi π 的马尔可夫过程 的平稳分布: { d π ( s ) } s ∈ S \{d_\pi(s)\}_{s\in\mathcal S} {dπ(s)}s∈S
d π ( s ) ≥ 0 d_\pi(s) \geq 0 dπ(s)≥0 且 ∑ s ∈ S d π ( s ) = 1 \sum\limits_{s\in\mathcal S}d_\pi(s) =1 s∈S∑dπ(s)=1
J ( w ) = E [ ( v π ( S ) − v ^ ( S , w ) ) 2 ] = ∑ s ∈ S d π ( s ) ( v π ( s ) − v ^ ( s , w ) ) 2 J(w) =\mathbb E[(v_\pi(S)-\hat v(S, w))^2]=\sum\limits_{s\in\mathcal S}\textcolor{blue}{d_\pi(s)}(v_\pi(s)-\hat v(s, w))^2 J(w)=E[(vπ(S)−v^(S,w))2]=s∈S∑dπ(s)(vπ(s)−v^(s,w))2
这个函数是加权平方误差。
由于访问频率越高的状态具有更高的
d
π
(
s
)
d_\pi(s)
dπ(s) 值,因此它们在目标函数中的权重也高于 访问频率越低 的状态。

——————
优化目标函数
最小化 梯度下降

用 随机梯度 替换 真实梯度, 避免 计算期望。
w t + 1 = w t + α t ( v π ( s t ) − v ^ ( s t , w t ) ) ∇ w v ^ ( s t , w t ) w_{t+1}=w_t+\alpha_t(v_\pi(s_t)-\hat v(s_t,w_t))\nabla _w\hat v(s_t, w_t) wt+1=wt+αt(vπ(st)−v^(st,wt))∇wv^(st,wt)
问题:
v
π
v_\pi
vπ 未知。——> 用 近似值 替换
方式一:基于 MC 学习。 用 episode 中从
s
t
s_t
st 开始的 折扣回报
g
t
g_t
gt 替换
v
π
(
s
t
)
v_\pi(s_t)
vπ(st)。
即
w
t
+
1
=
w
t
+
α
t
(
g
t
−
v
^
(
s
t
,
w
t
)
)
∇
w
v
^
(
s
t
,
w
t
)
w_{t+1}=w_t+\alpha_t(\textcolor{blue}{g_t}-\hat v(s_t,w_t))\nabla _w\hat v(s_t, w_t)
wt+1=wt+αt(gt−v^(st,wt))∇wv^(st,wt)
方式二: 基于 TD 学习。
v
π
(
s
t
)
v_\pi(s_t)
vπ(st)。
即
w
t
+
1
=
w
t
+
α
t
[
r
t
+
1
+
γ
v
^
(
s
t
+
1
,
w
t
)
−
v
^
(
s
t
,
w
t
)
]
∇
w
v
^
(
s
t
,
w
t
)
w_{t+1}=w_t+\alpha_t[\textcolor{blue}{r_{t+1}+\gamma \hat v(s_{t+1},w_t)}-\hat v(s_t,w_t)]\nabla _w\hat v(s_t, w_t)
wt+1=wt+αt[rt+1+γv^(st+1,wt)−v^(st,wt)]∇wv^(st,wt)

——————
如何选择
v
^
(
s
,
w
)
\hat v(s,w)
v^(s,w) ?
方式一: 线性近似。 v ^ ( s , w ) = ϕ T ( s ) w \hat v(s, w)=\phi^T(s)w v^(s,w)=ϕT(s)w
- 特征向量 ϕ ( s ) \phi(s) ϕ(s)。 系数
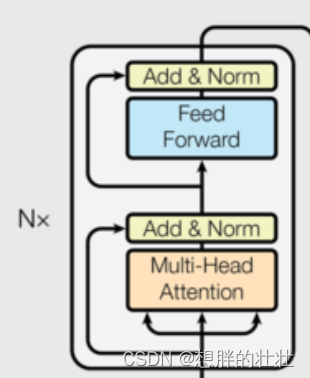
方式二: 非线性 近似。 神经网络。
- 神经网络的输入为 状态, 输出为 v ^ ( s , w ) \hat v(s, w) v^(s,w), 网络参数为 w w w。

线性近似的优缺点:
缺点:难以选择合适的特征向量。
优点:易于理解。
表格表示 是 线性函数近似 的 特例。
考虑 状态 s s s 的特征向量的特殊情况。
ϕ ( s ) = e s ∈ R ∣ S ∣ \phi(s)=e_s\in\mathbb R^{|\mathcal S|} ϕ(s)=es∈R∣S∣
e s e_s es: 第 s s sth 个数为 1 , 其它为 0 的向量。
v ^ ( s , w ) = ϕ T ( s ) w = e s T w = w ( s ) \hat v(s, w)=\phi^T(s)w=e^T_sw=w(s) v^(s,w)=ϕT(s)w=esTw=w(s)
w ( s ) w(s) w(s): w w w 的 第 s s sth 个数

——————
例子:
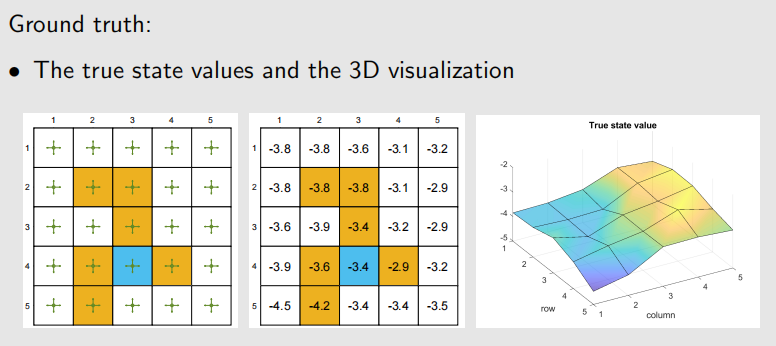

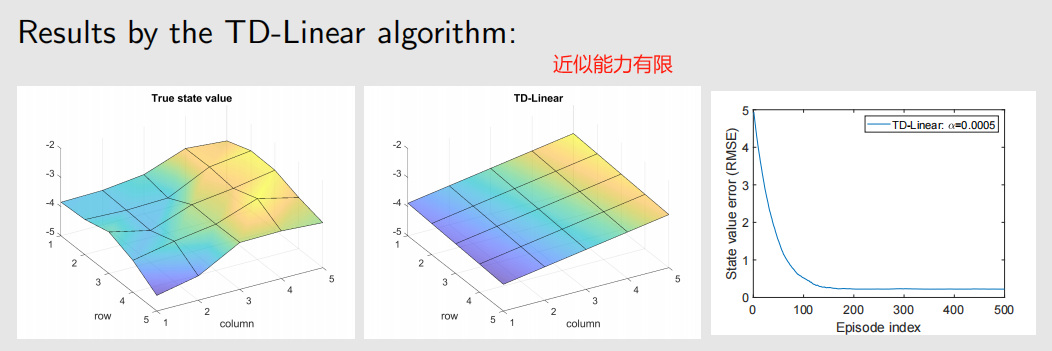

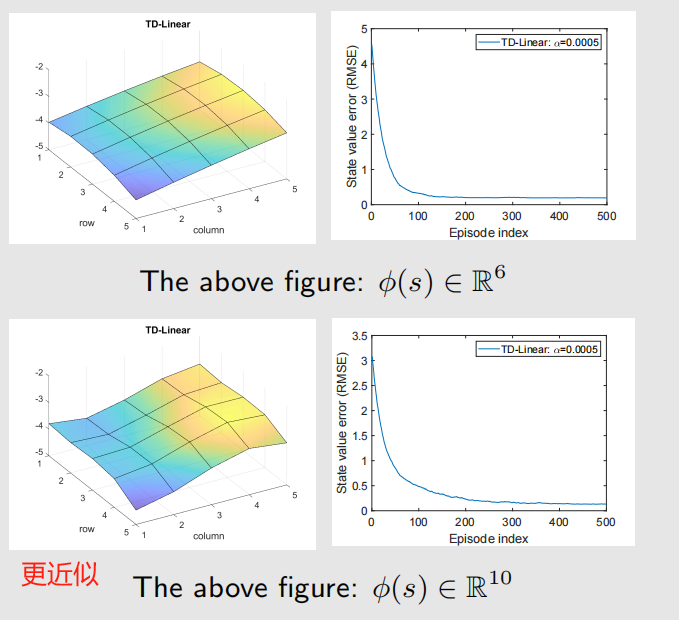
——————
TD-Linear 算法最小化的是 投影 贝尔曼误差。

P3 Sarsa + 值函数近似
w t + 1 = w t + α t [ r t + 1 + γ q ^ ( s t + 1 , a t + 1 , w t ) − q ^ ( s t , a t , w t ) ] ∇ w q ^ ( s t , a t , w t ) w_{t+1}=w_t+\alpha_t[r_{t+1}+\gamma\hat q(s_{t+1}, a_{t+1}, w_t)-\hat q(s_t,a_t,w_t)] \nabla_w\hat q(s_t, a_t, w_t) wt+1=wt+αt[rt+1+γq^(st+1,at+1,wt)−q^(st,at,wt)]∇wq^(st,at,wt)

Q 学习 + 函数近似
w t + 1 = w t + α t [ r t + 1 + γ max a ∈ A ( s t + 1 ) q ^ ( s t + 1 , a , w t ) − q ^ ( s t , a t , w t ) ] ∇ w q ^ ( s t , a t , w t ) w_{t+1}=w_t+\alpha_t[r_{t+1}+\gamma \textcolor{blue}{\max\limits_{a\in\mathcal A(s_{t+1})}}\hat q(s_{t+1},\textcolor{blue}{a} , w_t)-\hat q(s_t,a_t,w_t)] \nabla_w\hat q(s_t, a_t, w_t) wt+1=wt+αt[rt+1+γa∈A(st+1)maxq^(st+1,a,wt)−q^(st,at,wt)]∇wq^(st,at,wt)

8.4 Deep Q-leaning 【DQN】
Deep Q-learning、deep Q-network (DQN)
最成功地将 深度神经网络 引入强化学习的算法之一。
应用 和 方法
应用: 在一系列游戏控制上 达到人类控制的水平。
方法: 关键技术 后续被广泛使用。
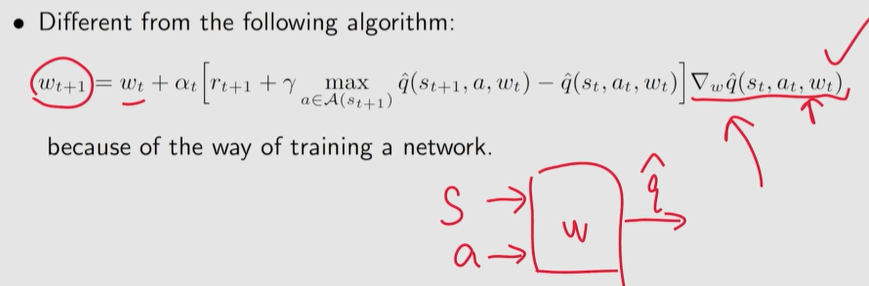
目标函数:

优化:

我们可以在计算梯度时假设 y y y 中的 w w w 是固定的(至少在一段时间内是固定的)。

使用两个网络, 分别 估计
w
w
w
主网络的
w
w
w: 一直更新
目标网络的
w
T
w_T
wT: 隔一段时间 更新

DQN 的基本思想是使用梯度下降算法最小化目标函数。
2 个重要技巧:
1、两个网络:一个主网络和一个目标网络。
实现细节:
令
w
w
w 和
w
T
w_T
wT 分别表示主网络和目标网络的参数。它们最初被设置为相同的。
在每次迭代中,我们从重放缓冲区中提取一小批样本
{
(
s
,
a
,
r
,
s
′
)
}
\{(s, a, r, s')\}
{(s,a,r,s′)}。
网络的输入包括状态
s
s
s 和动作
a
a
a,目标输出为
y
T
=
r
+
γ
max
a
∈
A
(
s
′
)
q
^
(
s
′
,
a
,
w
T
)
y_T =r+ \gamma \max\limits_{a\in \cal A(s') }\hat q(s',a,w_T)
yT=r+γa∈A(s′)maxq^(s′,a,wT)。然后,我们直接最小化 小批次
{
(
s
,
a
,
y
T
)
}
\{(s, a,y_T)\}
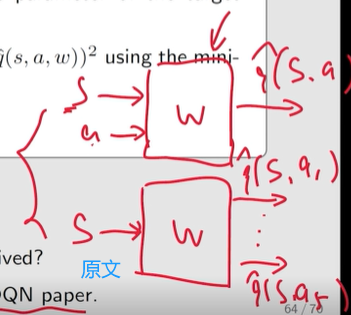
{(s,a,yT)} 上的 TD 误差或称为损失函数
(
y
T
−
q
^
(
s
,
a
,
w
)
)
2
(y_T - \hat q(s, a, w))^2
(yT−q^(s,a,w))2。
2、经验回放
replay buffer 回放缓冲 B = { ( s , a , r , s ′ ) } \mathcal B=\{(s, a, r, s^\prime)\} B={(s,a,r,s′)}
每次我们训练神经网络时,我们都可以从回放缓冲区中抽取一小批随机样本。
均匀分布 经验回放。
为什么 DQN 需要经验回放?为什么重播必须遵循均匀分布?

然而,样本并不是统一收集的,因为它们是由某些策略生成的。
为了打破后续样本之间的相关性,我们可以使用经验重放技术,从重放缓冲区中均匀地提取样本。
更充分地使用数据

再强大的算法 也需要 好的数据 才能 work。
8.6
目标函数 涉及到 状态的概率分布, 该分布通常选为 平稳分布。
为什么深度 Q-learning 需要经验回放?
原因在于 (8.37) 中的目标函数。特别是,为了很好地定义目标函数,我们必须指定
S
,
A
,
R
,
S
′
S, A, R, S'
S,A,R,S′ 的概率分布。
当
(
S
,
A
)
(S, A)
(S,A) 给定时,由系统模型确定
R
R
R 和
S
′
S'
S′ 的分布。
描述 状态-行为对
(
S
,
A
)
(S, A)
(S,A) 分布的最简单方法是假设它是均匀分布的。然而,状态-动作样本在实践中可能不是均匀分布的,因为它们是由行为策略作为一个序列生成的。为了满足均匀分布的假设,有必要打破序列中样本之间的相关性。为此,我们可以使用经验重放技术,从重放缓冲区中均匀地抽取样本。经验回放的一个好处是,每个经验样本可以被多次使用,这可以提高数据效率。
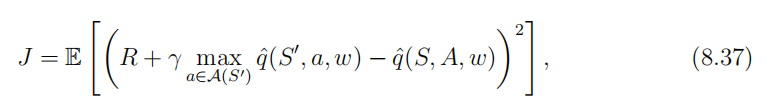
——————
习题笔记
表格表示 可以看作是 函数表示 的特例
难以直接计算目标函数的梯度:先固定目标函数中的一部分,这样求解梯度更容易。