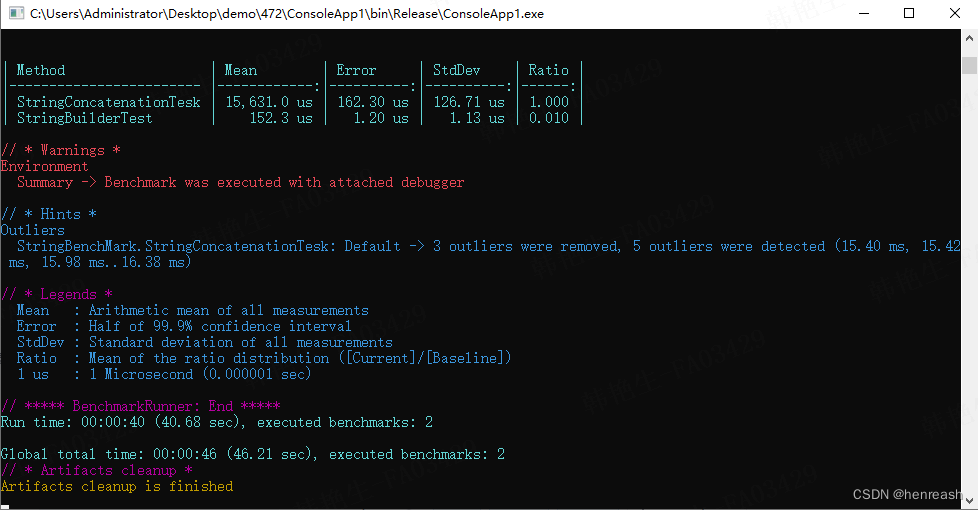
Description
有n种基础的投资项目,每一种的单位收益率为profitn,存在m种投资组合,限制每一种的投资总额不能超过invest_summ
每种投资组合中项目所需的单位投入是不同的,为costmn
求:使得收益率之和最高的每种项目投资的单位数
Input
- 两个整数:n(项目种类数,范围:1≤n<20),m(投资组合数,1≤m<20)
- 一行长度为n的2位小数:profitn(单位收益率,0<profitn<1)
- 一行长度为m的整数:invest_summ(某组合的限制投资总额,invest_summ>0)
- m行长度为n的整数:costmn(某组合中某项目的单位投入,costmn>0)
Output
- 输出n个以空格间隔的8位小数,表示每一个项目投资的单位量。
- 如果有多个最优解,输出任意一个。
Sample
#0
Input
Copy
4 3 0.13 0.75 0.25 0.44 20 7 50 5 3 2 1 2 1 1 1 7 12 9 2
Output
Copy
0.00000000 3.60000000 0.00000000 3.40000000
Hint
max Σprofit x
s.t. cost x<= invest_sum, x>=0

线性规划公式秒了
#include<iostream>
#include<cmath>
#include"stdio.h"
using namespace std;
#define M 10000
double kernel[110][310];
int m = 0, n = 0, t = 0;
void input()
{
cin>>n;
cin>>m;
// m = 3;
int i, j;
//初始化核心向量
for (i = 0; i <= m + 1; i++)
for (j = 0; j <= n + m + m; j++)
kernel[i][j] = 0;
for (i=1;i<=n;i++)
cin>>kernel [0][i];
for(i=1;i<=m;i++){
cin>>kernel[i][n+2];
}
for (i=1;i<=m;i++)
{
// cout<<" 不等式"<<i<<" ";
for (j=1;j<=n+2;j++)
{
if(j==n+1){
kernel[i][j]=1;
}
else if(j==n+2){
}
else{
cin>>kernel [i][j];
}
}
}
for (i = 1; i <= m; i++)
{
kernel[i][0] = kernel[i][n + 2];
kernel[i][n + 2] = 0;
}
//-1最大值
//1最小值
t = -1;
if (t == -1)
for (i = 1; i <= n; i++)
kernel[0][i] = (-1)*kernel[0][i];
for (i = 1; i <= m; i++)
{
kernel[i][n + i] = kernel[i][n + 1];
if (i != 1)
kernel[i][n + 1] = 0;
}
}
//算法函数
void comput()
{
int i, j, flag, temp1, temp2, h, k = 0, temp3[100];
double a, b[110], temp, temp4[110], temp5[110], f = 0, aa, d, c;
for (i = 1; i <= m; i++)
temp3[i] = 0.0000;
for (i = 0; i < 11; i++)
{
temp4[i] = 0.000;
temp5[i] = 0.0000;
}
for (i = 1; i <= m; i++)
{
if (kernel[i][n + i] == -1)
{
kernel[i][n + m + i] = 1;
kernel[0][n + m + i] = M;
temp3[i] = n + m + i;
}
else
temp3[i] = n + i;
}
for (i = 1; i <= m; i++)
temp4[i] = kernel[0][temp3[i]];
do {
for (i = 1; i <= n + m + m; i++)
{
a = 0;
for (j = 1; j <= m; j++)
a += kernel[j][i] * temp4[j];
kernel[m + 1][i] = kernel[0][i] - a;
}
for (i = 1; i <= n + m + m; i++)
{
if (kernel[m + 1][i] >= 0) flag = 1;
else
{
flag = -1;
break;
}
}
if (flag == 1)
{
for (i = 1; i <= m; i++)
{
if (temp3[i] <= n + m) temp1 = 1;
else
{
temp1 = -1;
break;
}
}
if (temp1 == 1)
{
// cout << " 此线性规划的最优解存在!" << endl << endl << " 最优解为:" << endl << endl << " ";
for (i = 1; i <= m; i++)
temp5[temp3[i]] = kernel[i][0];
for (i = 1; i <= n; i++)
f += t * kernel[0][i] * temp5[i];
for (i = 1; i <= n; i++)
{
if(i==1){
printf("%.8f",temp5[i]);
}
else{
printf(" %.8f",temp5[i]);
}
// cout << "x" << i << " = " << temp5[i];
// printf("")
// if (i != n)
// cout << ", ";
}
cout<<endl;
// cout << " ;" << endl << endl << " 最优目标函数值f= " << f << endl << endl;
// printf("%.6f\n",f);
return;
}
else
{
// cout << " 此线性规划无解" << endl << endl;
return;
}
}
if (flag == -1)
{
temp = 100000;
for (i = 1; i <= n + m + m; i++)
if (kernel[m + 1][i] < temp)
{
temp = kernel[m + 1][i];
h = i;
}
for (i = 1; i <= m; i++)
{
if (kernel[i][h] <= 0) temp2 = 1;
else {
temp2 = -1;
break;
}
}
}
if (temp2 == 1)
{
// cout << "此线性规划无约束";
return;
}
if (temp2 == -1)
{
c = 100000;
for (i = 1; i <= m; i++)
{
if (kernel[i][h] != 0) b[i] = kernel[i][0] / kernel[i][h];
if (kernel[i][h] == 0) b[i] = 100000;
if (b[i] < 0) b[i] = 100000;
if (b[i] < c)
{
c = b[i];
k = i;
}
}
temp3[k] = h;
temp4[k] = kernel[0][h];
d = kernel[k][h];
for (i = 0; i <= n + m + m; i++)
kernel[k][i] = kernel[k][i] / d;
for (i = 1; i <= m; i++)
{
if (i == k)
continue;
aa = kernel[i][h];
for (j = 0; j <= n + m + m; j++)
kernel[i][j] = kernel[i][j] - aa * kernel[k][j];
}
}
} while (1);
return;
}
int main()
{
input();
for(int i=1;i<n;i++){
for(int j=1;j<m+2;j++){
// cout<<kernel[i][j]<<" ";
}
// cout<<endl;
}
comput();
// int a = 0;
// scanf("%d", &a);
// cout<<f<<endl;
return 0;
}