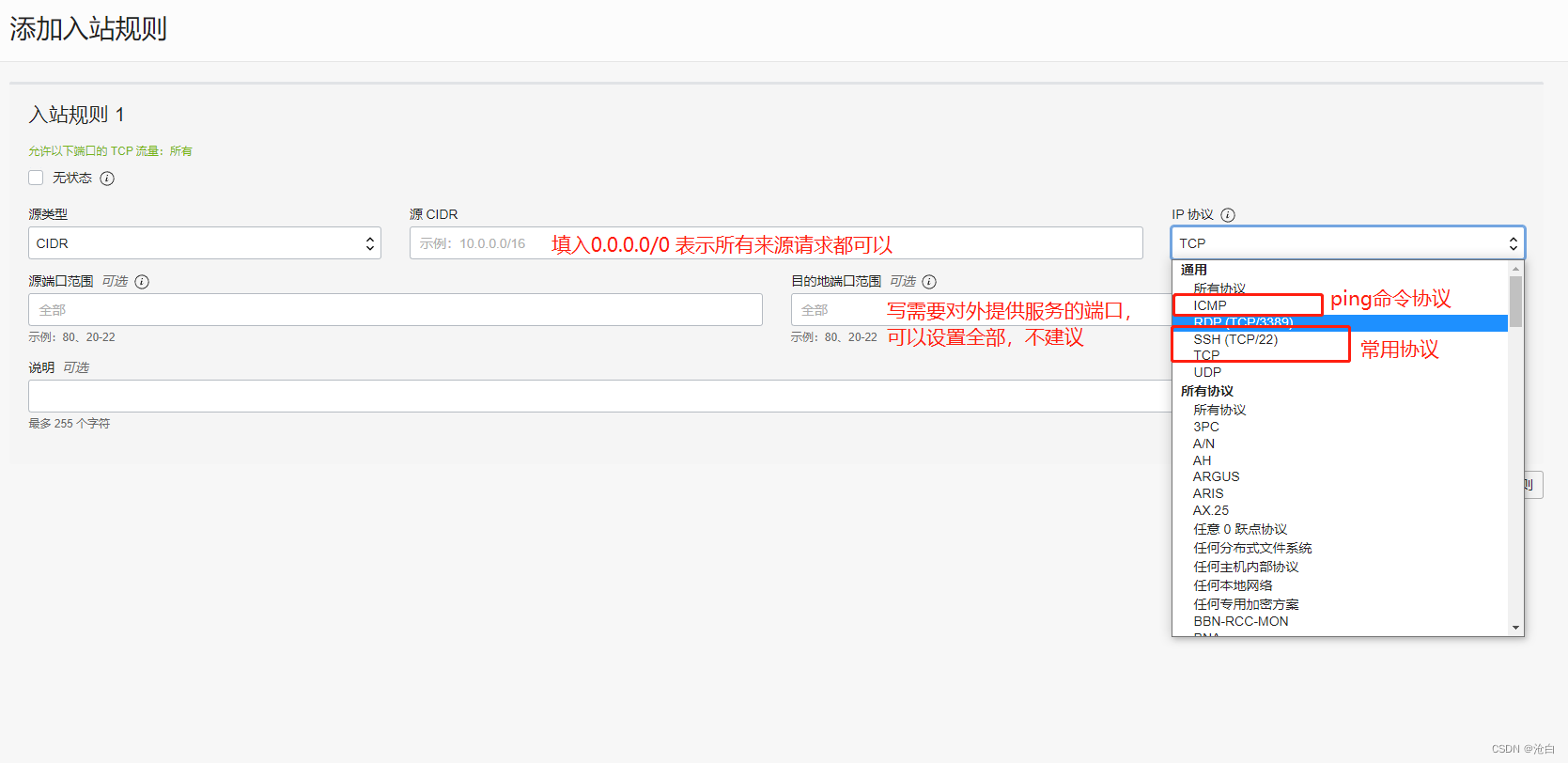
本节介绍利用根轨迹法分析系统性能发热方法
本节介绍根轨迹校正

---

利用根轨迹分析系统性能

利用根轨迹分析系统性能，主要还是看系统性能与零极点之间的关系。
有一下几个基本步骤：

1. 绘制系统根轨迹
2. 根据题意确定闭环极点
3. 确定闭环零点
4. 保留主导极点，利用零点极点法估算系统性能

主导极点法

对于稳定的高阶系统，闭环极点离虚轴越远，对应的相应分量衰减越快。所以即使系统存在多个零极点，也可以简化掉这些衰减太快的。
如果距离虚轴最近的极点周围没有零点，而其他极点有远离虚轴，就称这个闭环极点为主导极点。可以用这个主导极点近似一个二阶系统
如果一个极点旁边很近就有零点，称这种情况为“偶极子”，这时零点和极点对系统带来的影响可以认为相互低效，因此这种偶极子也需要忽略。

来看这个例题（主要是第三问）：

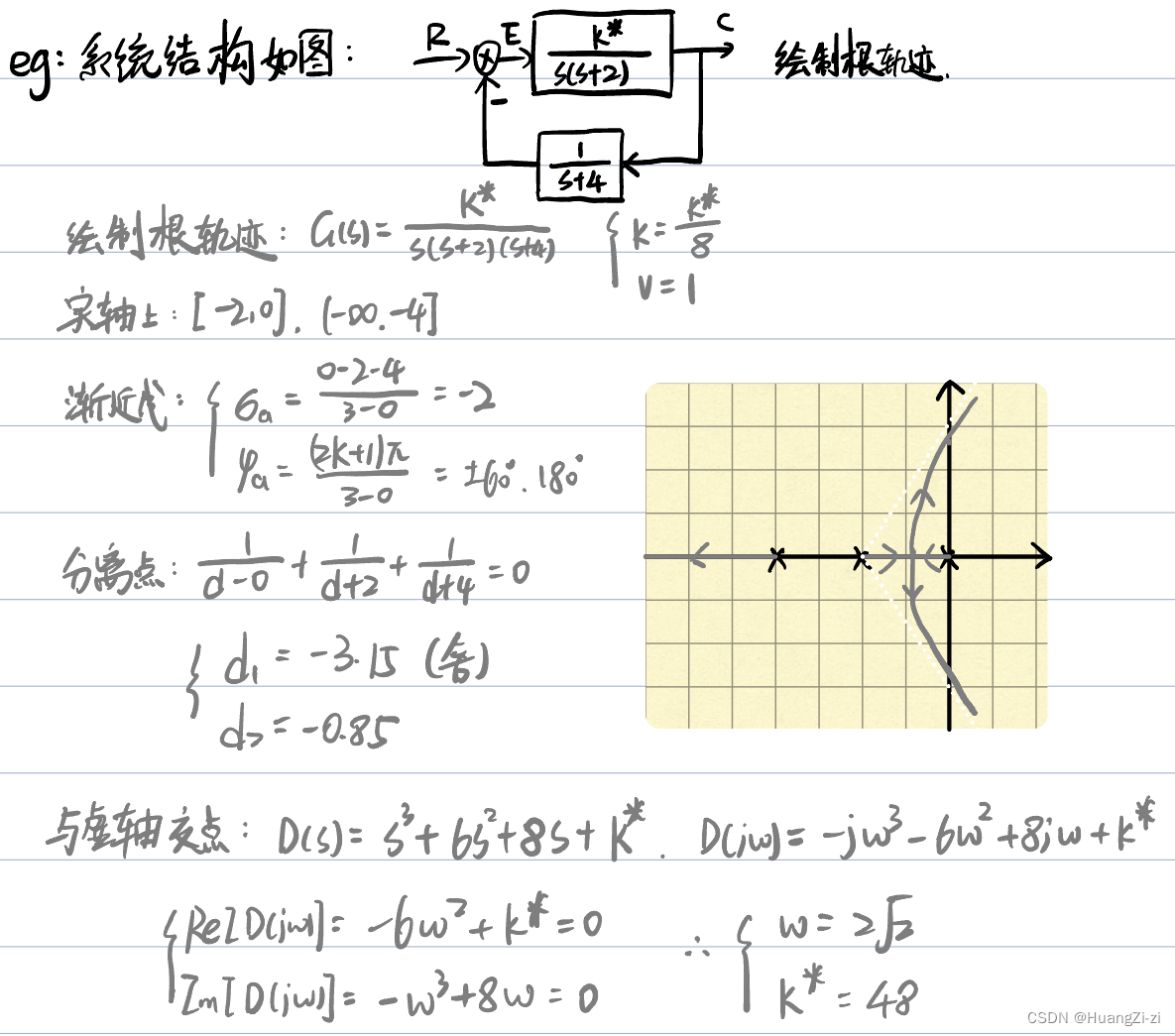
画根轨迹啥的，不再赘述了

第一问求稳定状态下增益的取值范围

回顾一下，稳定充要条件所有极点都在虚轴左侧
欠阻尼表明极点不在实轴上也不在虚轴上

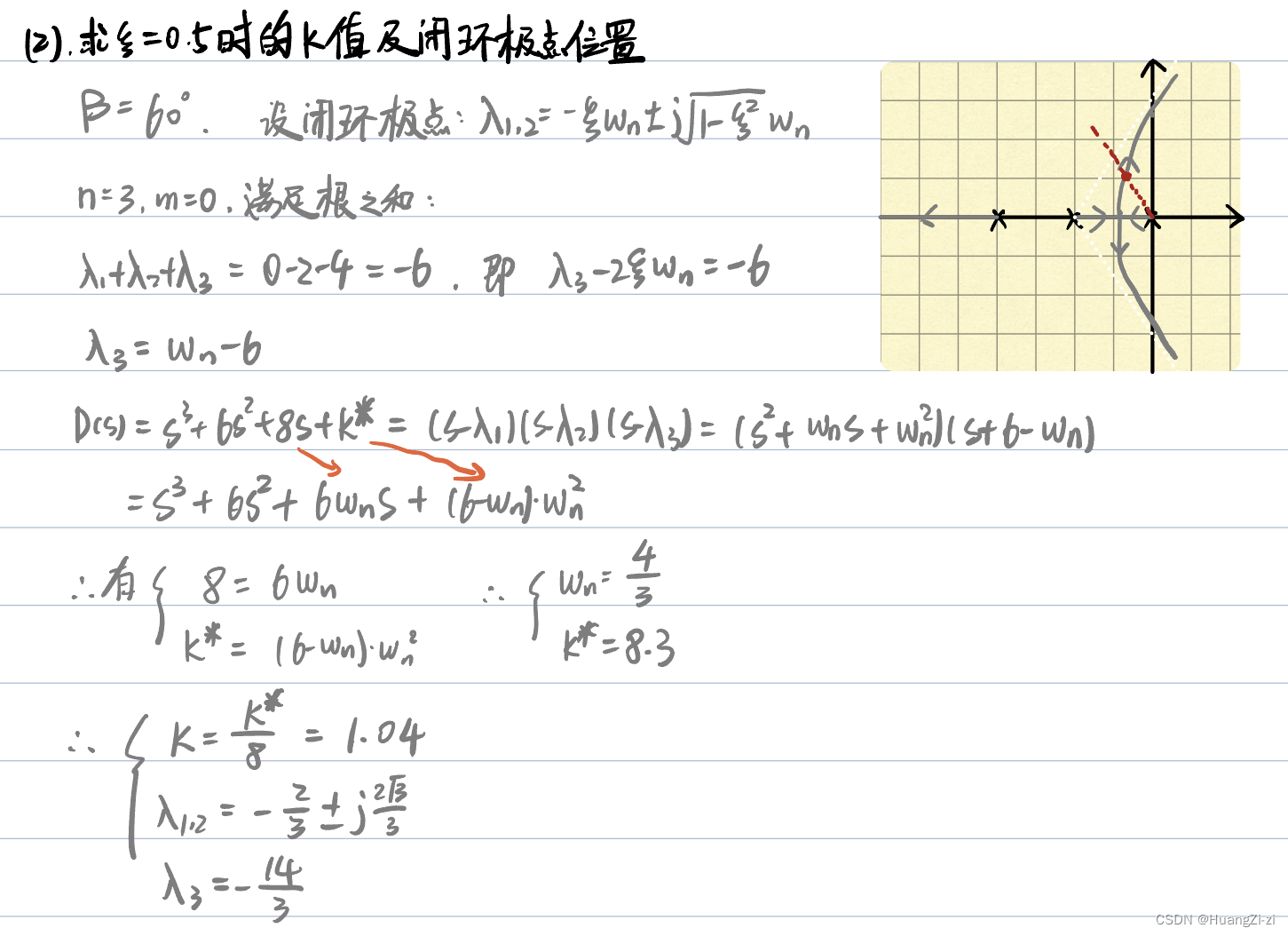
第二问让求某一个极点的具体参数。比较通用的方法就是当这个系统是二阶系统然后把极点设出来，再结合根轨迹的性质求点的座标。

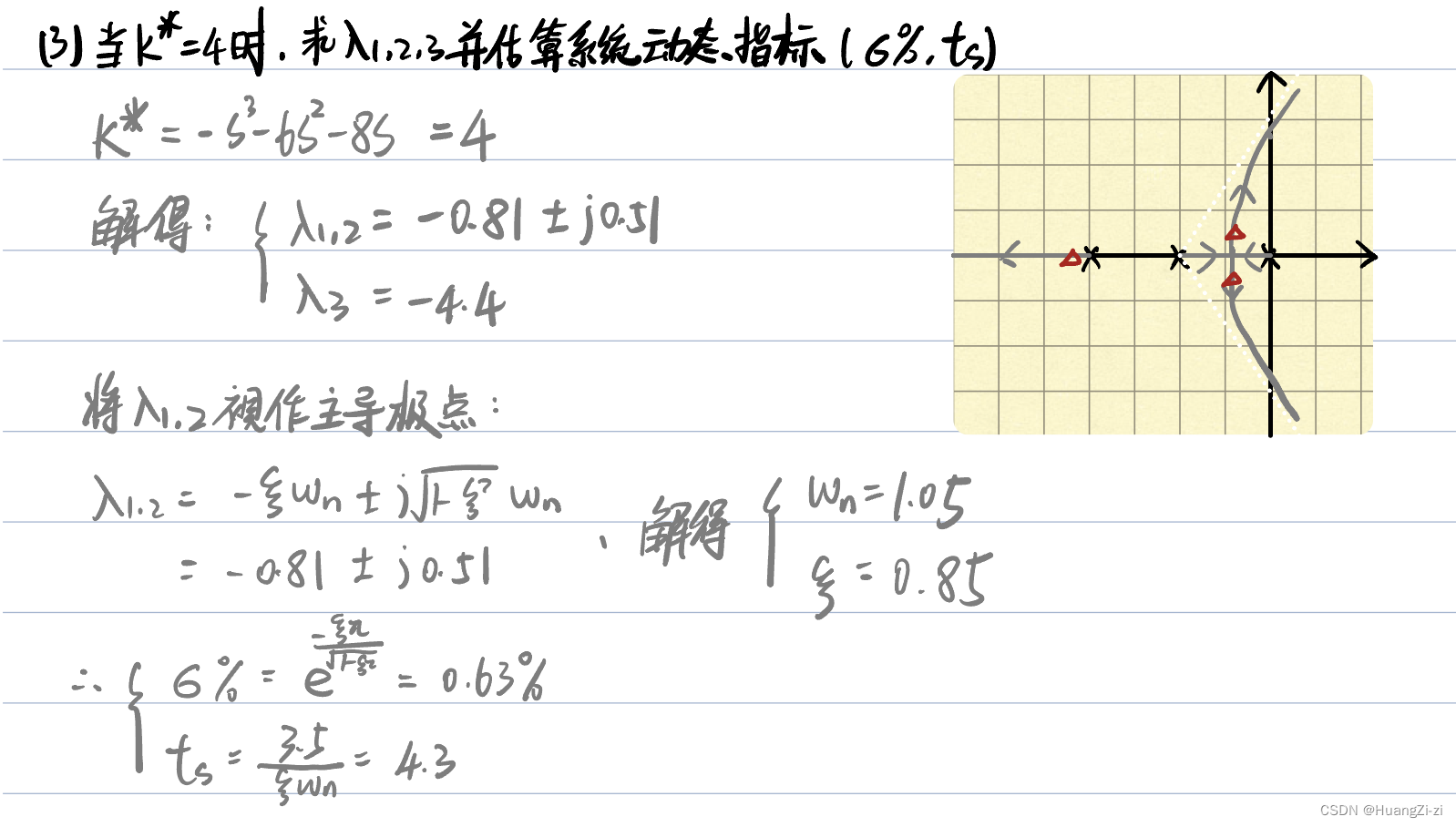
第三问要求估算性能指标。首先找出极点所在，根据到虚轴的距离，把最近的那一个作为主导极点。然后就可以按照二阶系统来求解。这里是估算，就不需要考虑零点和非主导极点了。

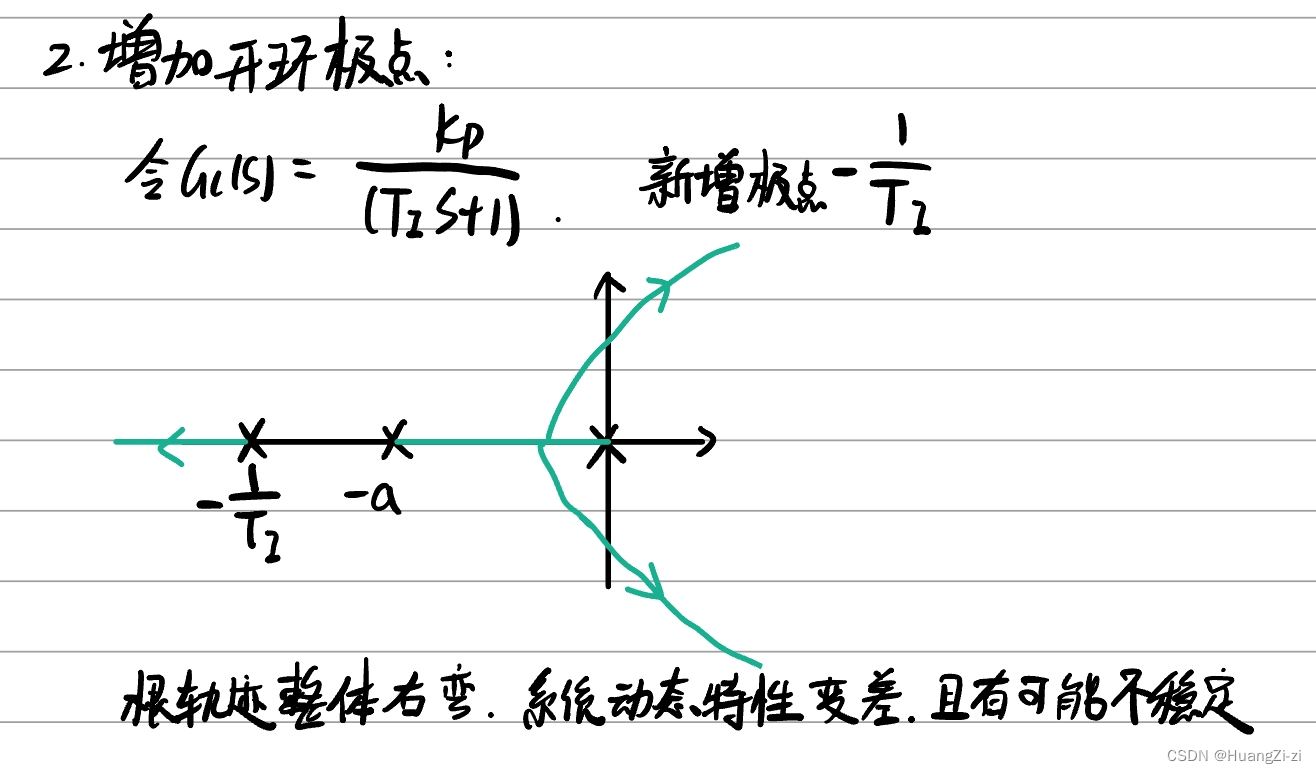
增加零极点对系统的影响

增加开环零点：有利于系统稳定和动态品质

增加开环极点：不利于系统稳定和动态品质

通过这个例子感受一下：

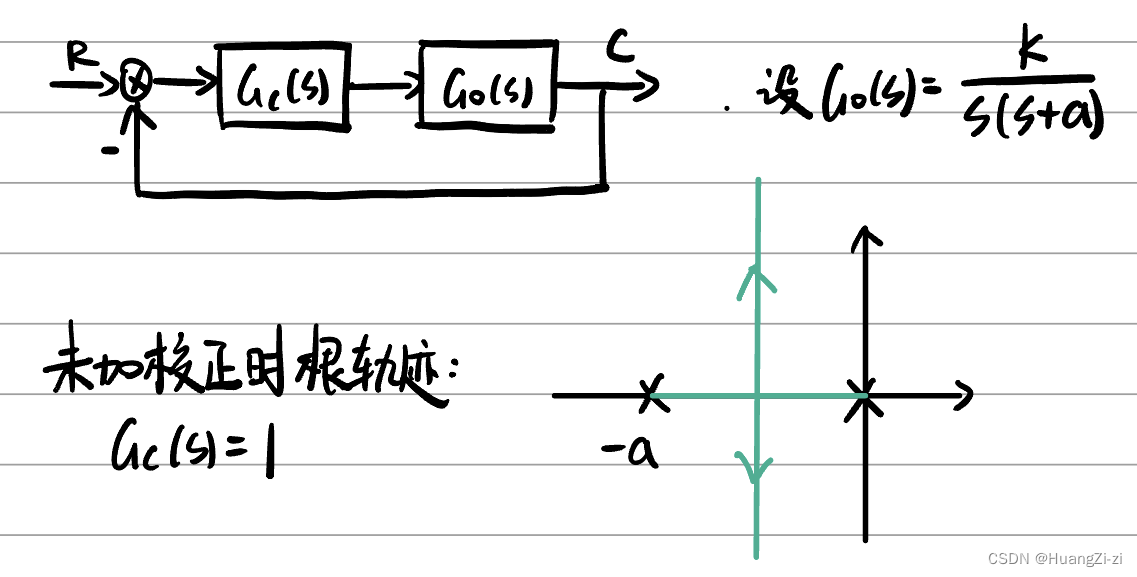
增加一个开环零点：

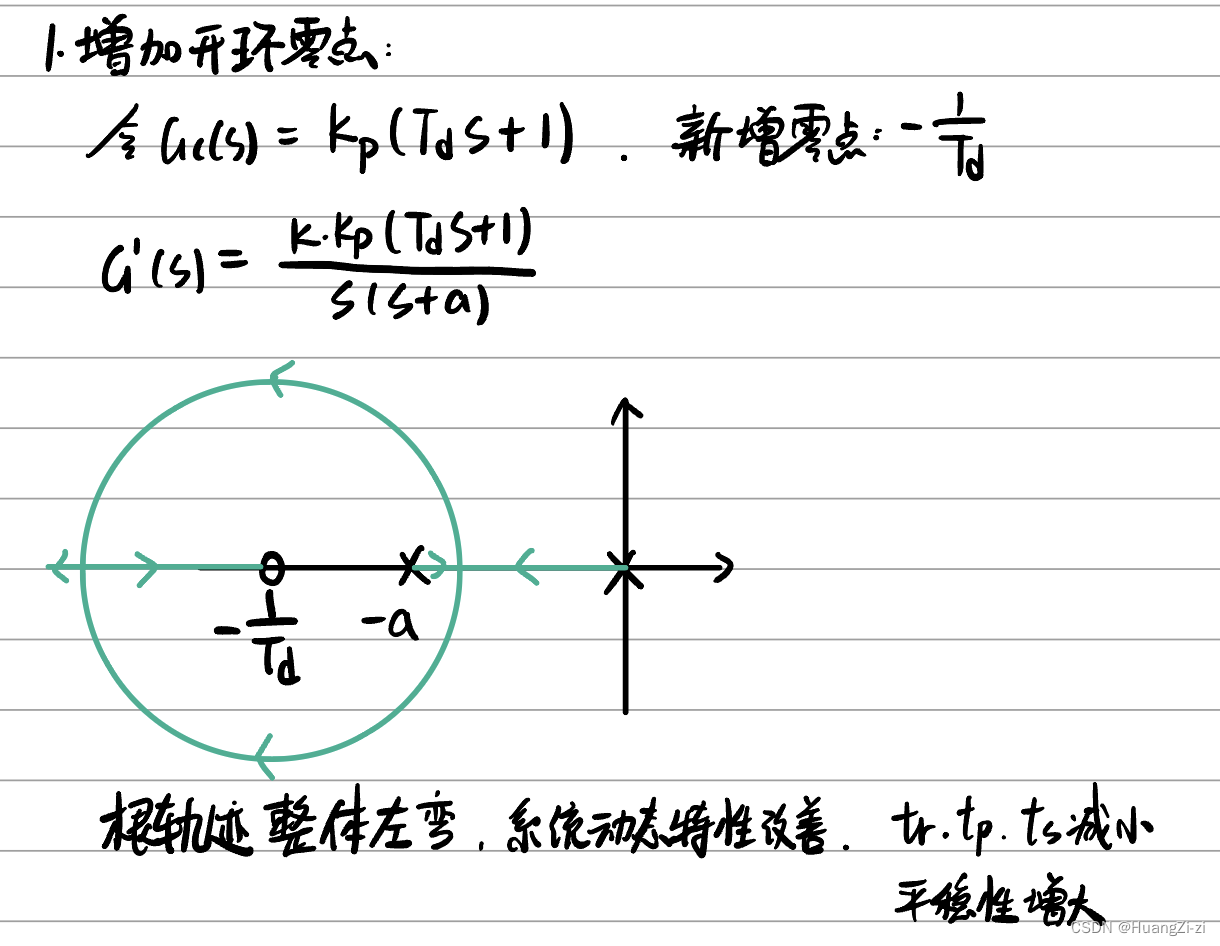
增加一个开环极点：

再来看一个稍复杂一些的例子：

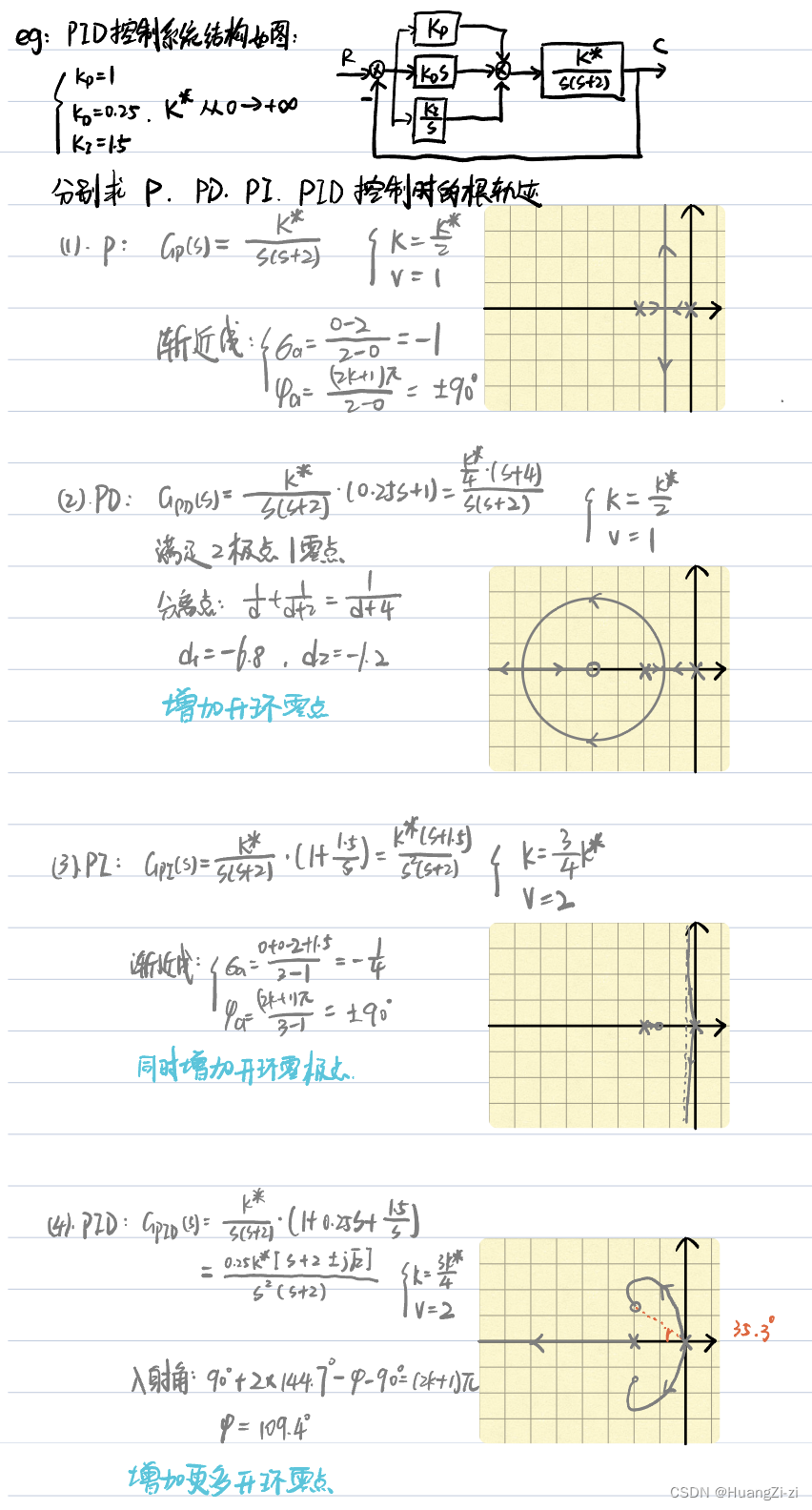
对比P和PD，增加开环零点之后根轨迹左移，动态性能提升。
对比P和PI，系统型别提高，跟踪输入的能力提高。
对比PD和PI，由于增加开环极点，动态性能变差。
对比PI和PID，再增加开环零点，同样根轨迹左移，动态性能提升。

根轨迹校正

利用根轨迹法校正系统，使原本不满足要求的系统现在满足要求。
利用根轨迹法设计串连校正装置的基本思路：根据要求，设计主导极点，通过校正装置，使根轨迹通过主导极点，并保证设计的主导极点可以看成主导极点。

串连超前校正

「建议先学习频域校正，再来看这个内容，理解会更深」

原理与步骤

原理

如果期望的主导极点位于未校正系统根轨迹的左边，可以使用超前校正。超前校正装置零点离虚轴近，起主导作用，使系统根轨迹左移。极点离虚轴远，避免影响性能。

在图中定义$\phi$和$\gamma$，以及表示极点的时候定义的$\beta$，就可以用三角函数解出零点、极点的位置了。

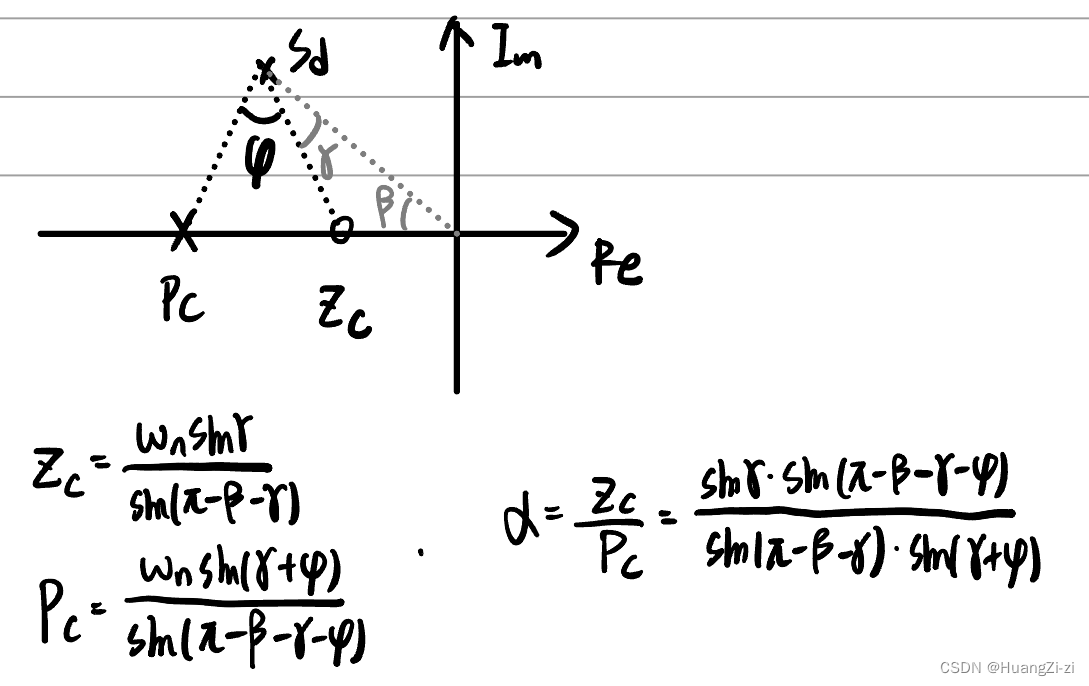
给定一个$\phi$，零极点位置并不是完全确定的。这里介绍的是使超前校正装置零点极点距离最远（$\alpha$最大）的一种方法：

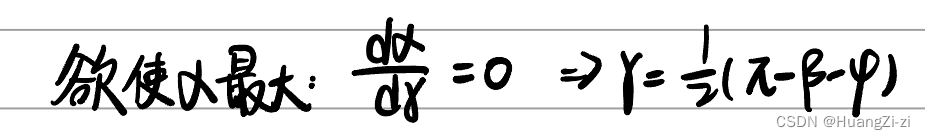
这样确定了$\gamma$，就可以唯一确定出零极点的位置了。

使用三角函数解比较严谨，实际使用的时候也可以按角度画图量长度。

超前校正的步骤

1. 有给定性能指标，求理想主导极点
2. 画未校正系统的根轨迹，确定校正方案
3. 求$\phi 、\gamma$，确定零极点位置，确定校正装置
4. 校验

超前校正例题

第一步求理想主导极点。

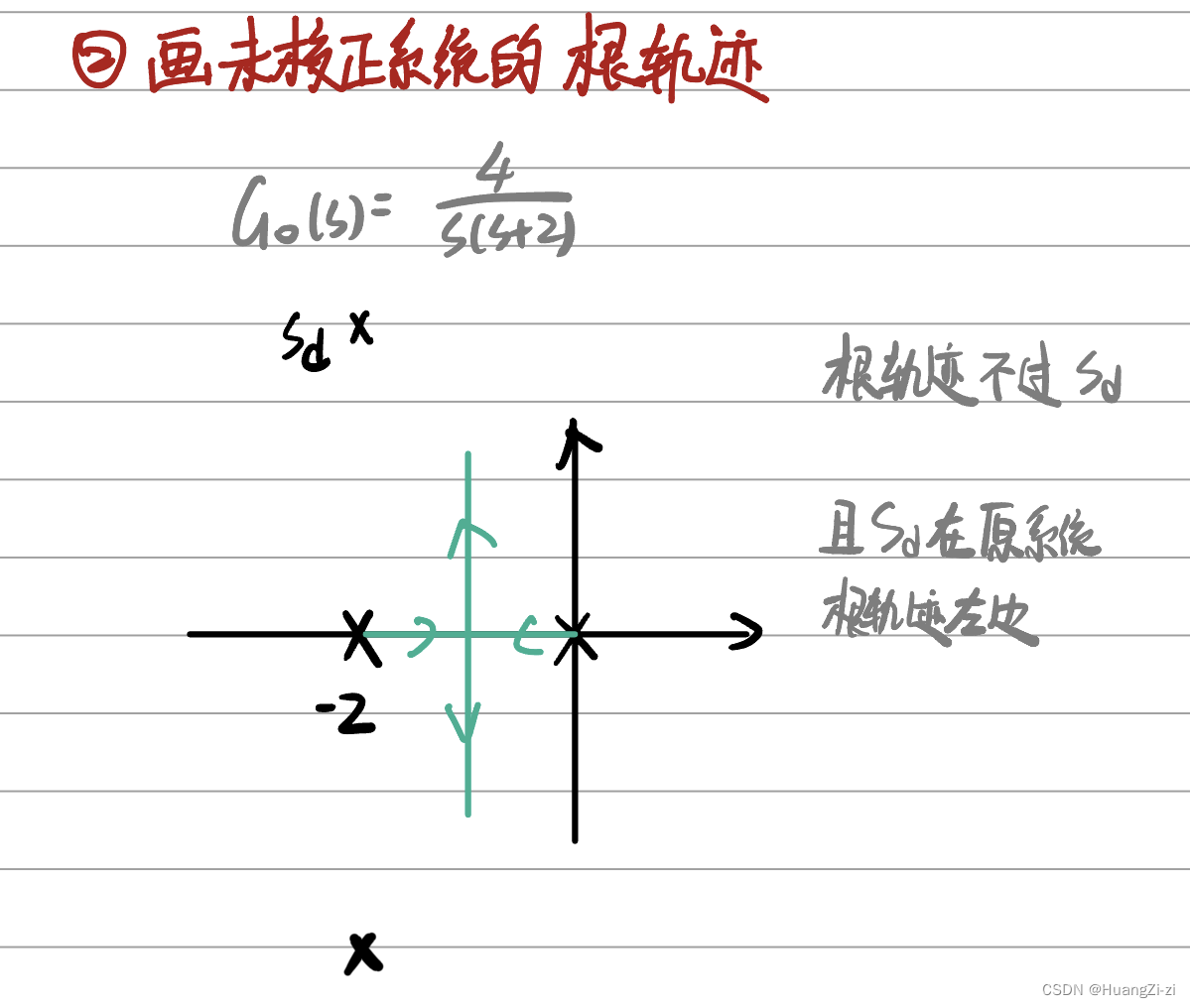
虽然系统已经给了一个根轨迹增益4，但我们可以把这个4换回K，画出这个根轨迹。改变的K由校正环节补偿。
画出原系统的根轨迹，发现根轨迹在理想主导极点右侧，可以用超前校正使根轨迹左移，因此选定校正方案

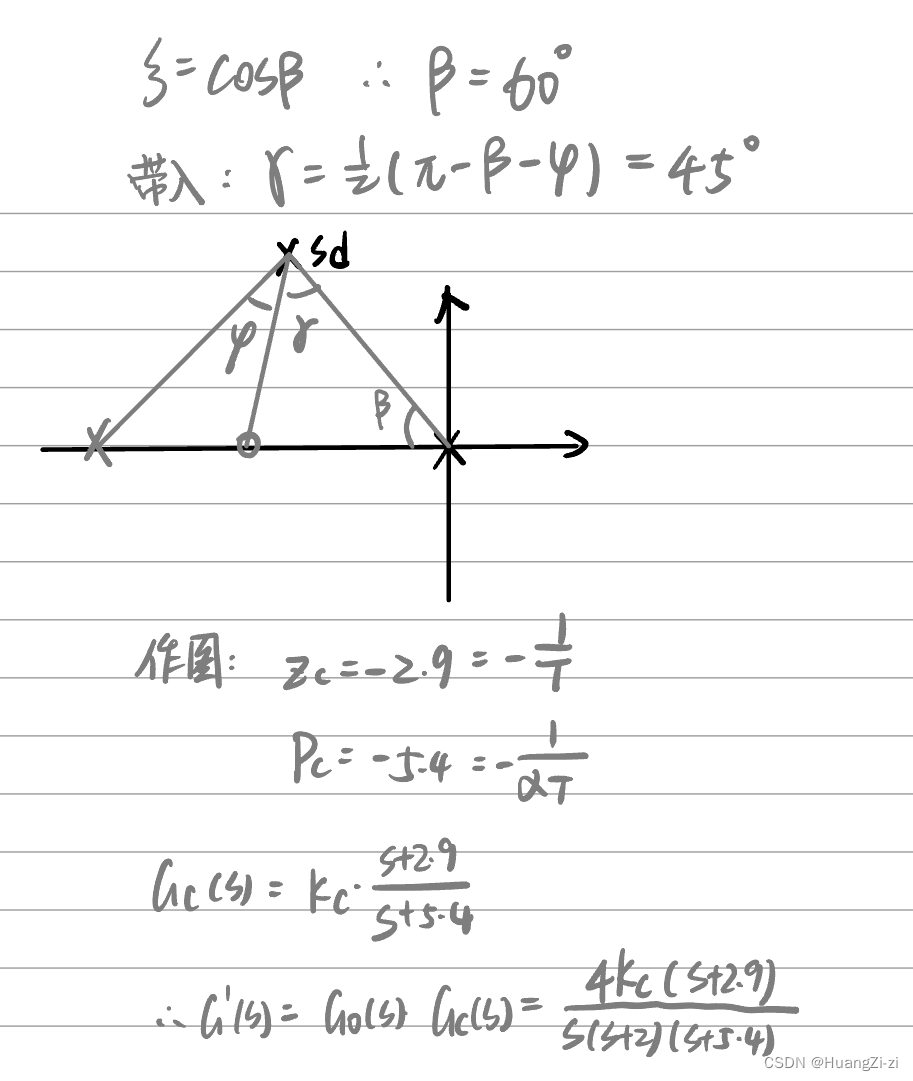
因为题目给出了原系统的开环增益是4，而为了在理想主导极点处满足幅值条件，就需要由校正系统补偿K值。

校验也不需要特别的计算，只需要看闭环系统的零极点分布，是不是理想主导极点真的是主导极点就可以了。

串连滞后校正

当系统已经有比较满意的暂态性能，需要提高稳态性能的时候，选用滞后校正。滞后校正实质为增加一对开环偶极子，在基本不改变根轨迹位置的情况下，增大开环增益，改善稳态特性。

附加开环偶极子的作用

原理与步骤

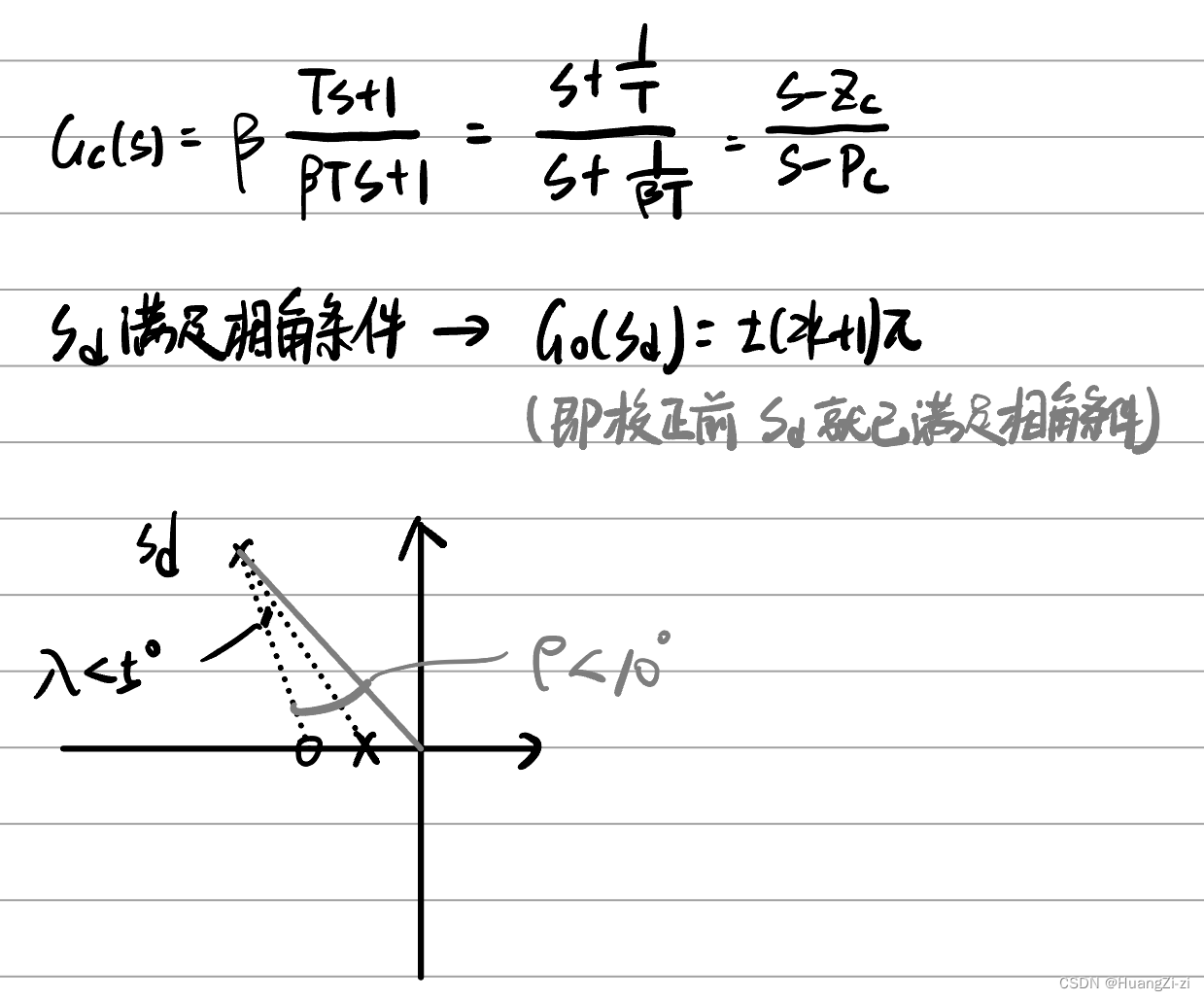
如图定义$\lambda$和$\rho$，在允许的取值范围里面取值，就可以用三角函数解出零极点位置，设计出校正装置了

步骤

1. 由期望性能指标求期望主导极点$s_d$
2. 画原系统根轨迹，确定校正方案
3. 求$\beta$，确定校正系统
4. 画新根轨迹，校验

滞后校正例题

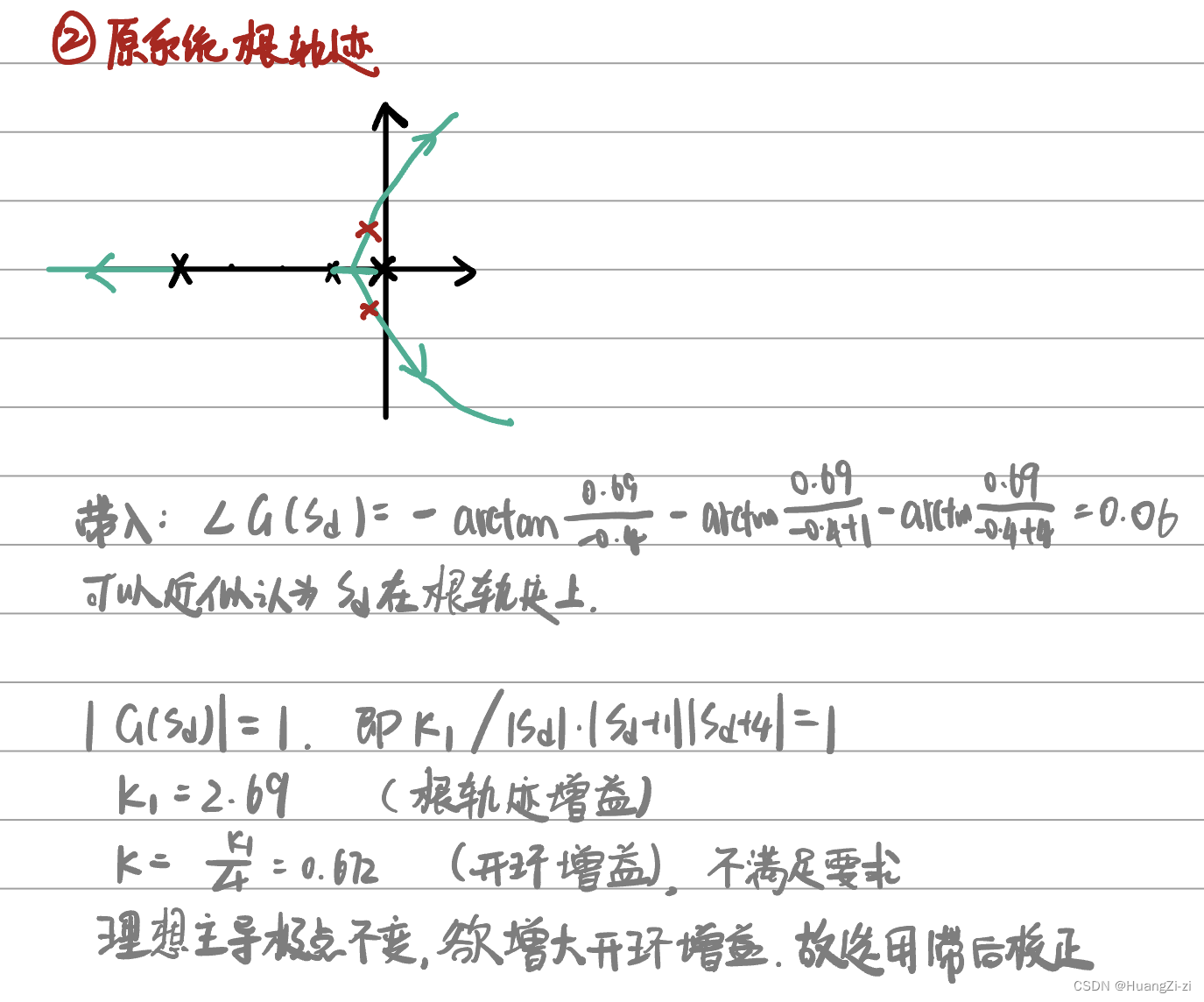
原根轨迹已经过理想主导极点了，但是增益不够，所以用滞后校正提高开环增益

开环增益提高$\beta$倍，根据三角关系设计出零点和极点，可以写出校正环节的传递函数

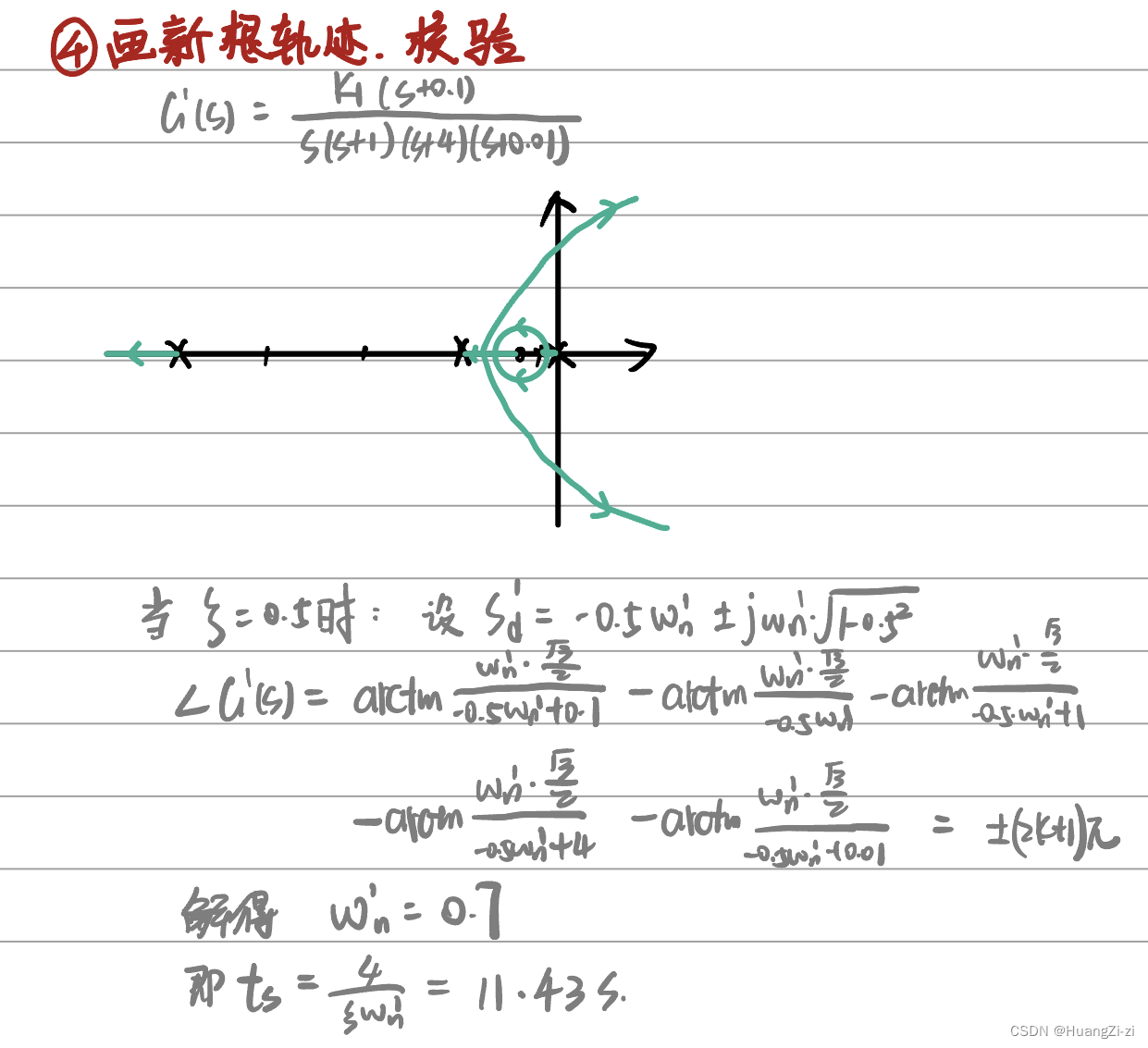
虽然$\lambda \le 5°$，但总归是有影响的，这个影响要实际消除比较难，所以如果误差允许的话就让它存在好了。