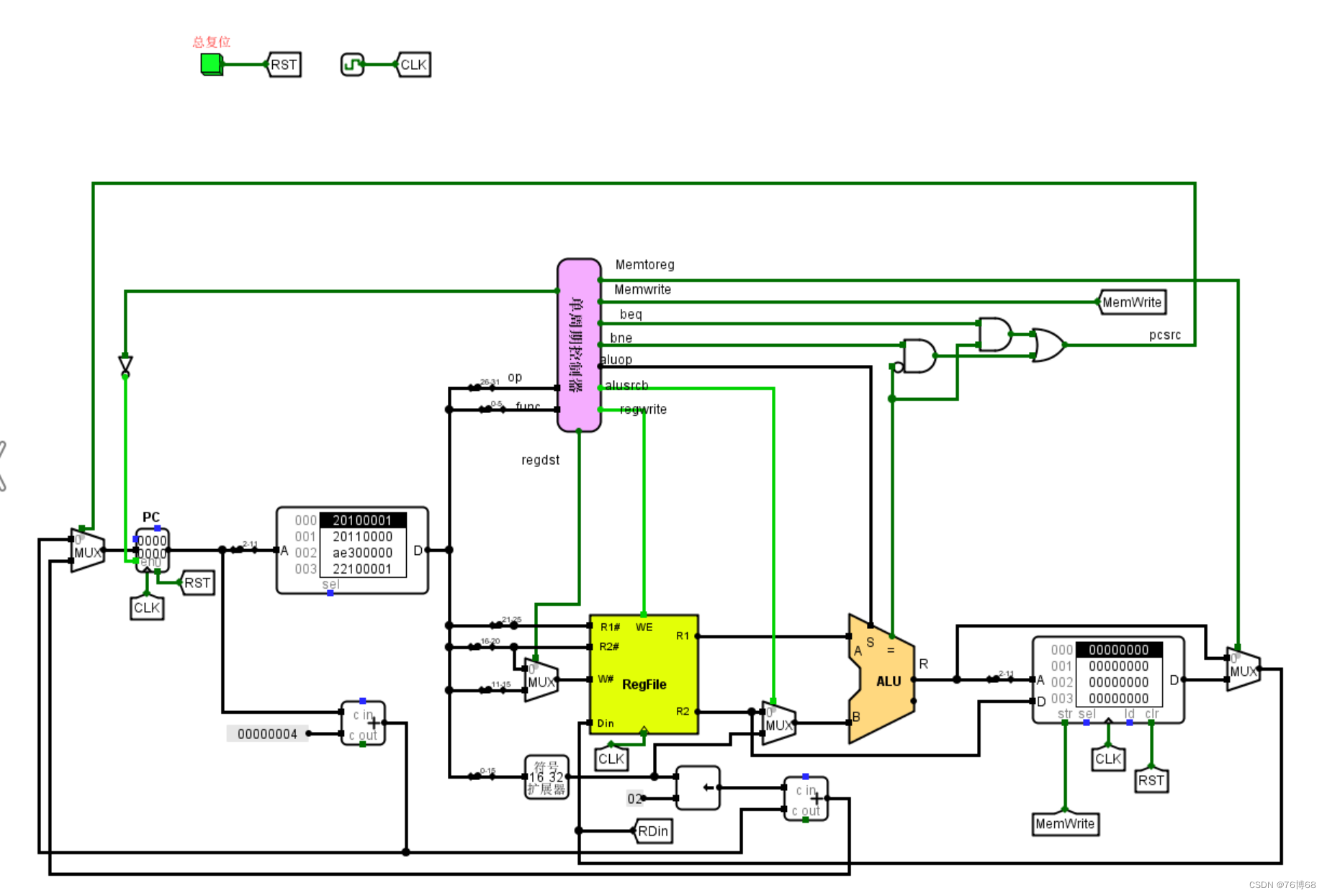
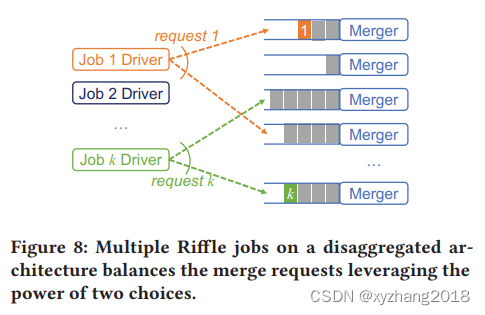
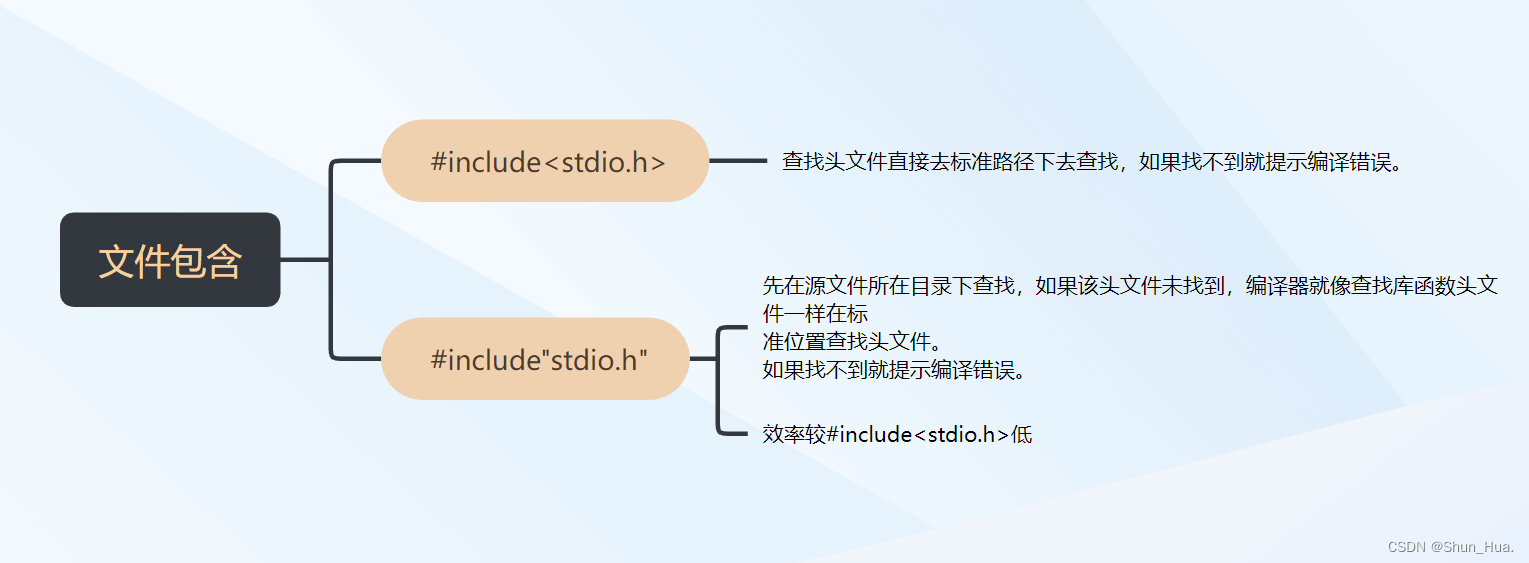
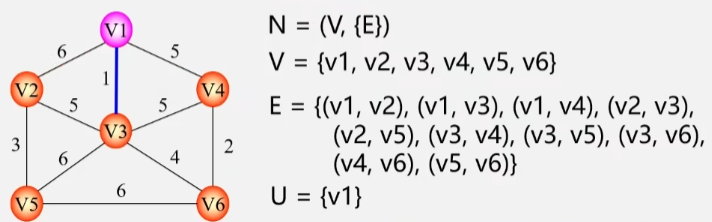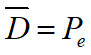文章目录
- 生成树及其构造
- 生成树的特点
- 无向图的生成树
- 6.6.1 最小生成树
- 最小生成树及其典型应用
- MST性质
- 构造最小生成树
- 1. Prim(普里姆)算法
- 2. Kruskal(克鲁斯卡尔)算法
- 两种算法比较
- 6.6.2 最短路径
- 最短路径问题
- 1. Dijkstra(迪杰斯特拉)算法
- 迪杰斯特拉算法步骤
- 2. Floyd(弗洛伊德)算法
- 弗洛伊德算法步骤
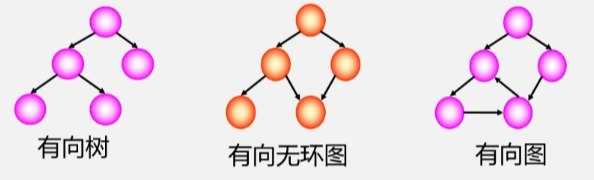
- 有向无环图及其应用
- 6.6.3 拓扑排序
- 拓扑排序的方法
- 检测 AOV 网中是否存在环
- 6.6.4 关键路径
- 用AOE网表示工程计划
- 求解关键路径
- 确定关键路径
- 求关键路径步骤
其中:拓扑排序以及关键路径针对的是一种特殊的图,称作有向无环图。
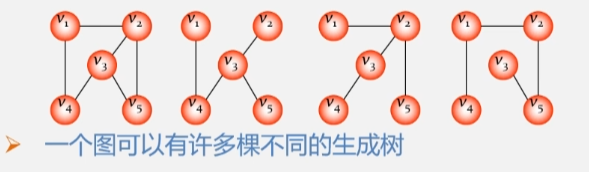
生成树及其构造
生成树:
- 图中所有顶点均由边连接在一起,但是不存在回路的图。
- 包含无向图 G 所有顶点的极小连通子图。
- 极小连通子图:
- 顶点的边数目在这个连通子图中的数目已经达到最小。
- 如果在该图中删除任何一条边,则子图不再连通,如果在该图中增加一条边,则图直接构成回路。
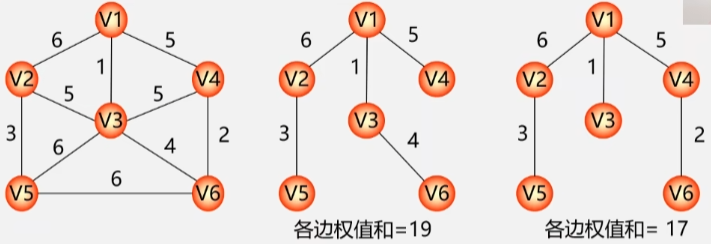
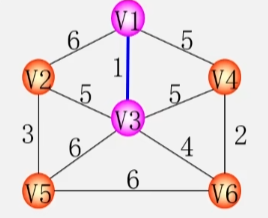
如:图右就是由包含图左所有顶点的极小连通子图。
生成树的特点
-
生成树的顶点个数与图的顶点个数相同。
-
生成树是图的极小连通子图,去掉一条边则非连通。
-
一个有 n 个顶点的连通图的生成树有 n-1条边。
- 但是含有 n 个顶点 n-1 条边的图不一定是生成树。
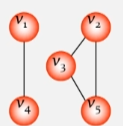
- 但是含有 n 个顶点 n-1 条边的图不一定是生成树。
-
在生成树中再增加一条边则必然形成回路。
无向图的生成树
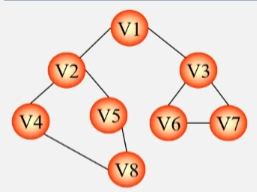
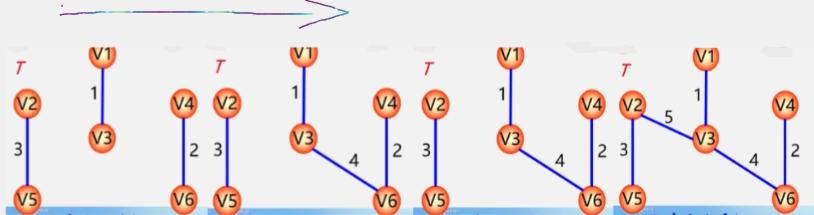
既然一棵生成树需要包含图中所有的顶点,那么就对这个图进行遍历。在访问的过程中,把走过的这些边加到生成树上,就可以得到生成树了。
深度优先生成树
- 利用深度优先遍历的方法,遍历下图。
- 将图中由蓝颜色的边和所有的顶点构成的图抽出来。
- 这个连通子图就是我们要搞定的生成树了。
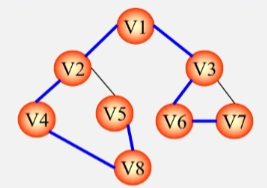
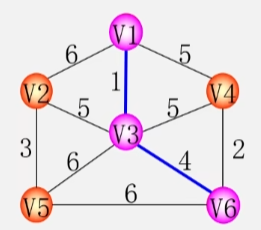
广度优先生成树
- 从 V1 顶点出发去访问它的所有邻接点 V2 V3。
- 依次访问 V2 的所有邻接点 V4 V5,以及 V3 的邻接点 V6 V7,最后访问 V4 的邻接点 V8。
- 此时根据走过的路径以及所有的顶点,也得到了了一棵生成树。
6.6.1 最小生成树
最小生成树及其典型应用
- 通过一个带权值的无向网,可以构造多棵不同的生成树。
- 这些生成树当中都包含有 n个顶点和n-1条边。
最小生成树:
- 给定一个无向网络,在该网的所有生成树中,使得各边权值之和最小的那棵生成树称为该网的最小生成树,也叫最小代价生成树。
最小生产树的意义
- 将所有的顶点都保持连通,边数达到最少且没有回路,
- 将所有的顶点连接起来所需要的边的权值最小。
最小生成树的典型用途
- 欲在 n 个城市之间建立通信网,则 n 个城市应该铺设 n-1 条线路。
- 但因为每条线路都会有对应的经济成本(边的权值),而 n 个城市最多有 n(n-1) / 2 条线路,那么,如何选择 n-1 条线路,才能使总费用最少?
显然此联通网就是一棵生成树
MST性质
- 构造最小生成树 Minimum Spanning Tree
- 构造最小生成树的算法很多,其中多数算法都利用率 MST 的性质。
- 后面要介绍的 Prim算法 和 Kruskal算法 都是使用的MST性质。
MST性质:
- 设 N = (V,E) 是一个连通网,U 是顶点集 V 的一个非空子集。
- 若边(u,v)是一条具有最小权值的边,其中 u ∈ U,v ∈ V-U,则必定存在一棵包含(u,v)的最小生成树。
举个例子
假设有个图 N,包含 V 个顶点,以及 E 条边。
- U 是顶点 V 的一个非空子集。
- 假设现在子集 U 中只有一个顶点 V1。
- 那么剩下的差集就是所有的顶点减去这个 V1,剩下 5 个顶点就在 V-U 这个集合中
- 假设现在存在一条有着最小权值的边,这个边是 u 到 v 之间的边。
- u 在 U 集合中,v 则在 V-U 集合中,从 u 到 v 中有从 V1 到 V2 、V3 和 V4 三个顶点的边。
- 其中:V1 到 V3 之间的这条边权值最小,那么这条边一定会包含在某一棵最小生成树当中。
- 反过来说:在构造最小生成树的时候,把权值最小的边包含进来
MST性质解释:
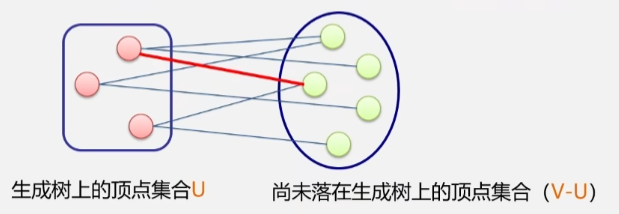
- 在生成树的构造过程中,图中 n 个顶点分别属于两个集合:
- 已经落在生成树上的顶点集:U。
- 尚未落在生成树上的顶点集:V-U。
- 接下来则应该再所有连通 U 中顶点 V-U 中顶点的边中选取权值最小的边。
- 现在有不在生成树上的顶点集合 V-U,和已经在生成树上的顶点集合 U。
- 如果从已经在生成树上的顶点,到还没有在生成树上的顶点之间存在着很多边。其中有一条边的权值最小。
- 在构造生成树的时候,就将这条边加进去。
- 前提是生成树不能有回路.
- 如果出现了回路,则继续选择下一条权值最小的边,加进生成树。
构造最小生成树
构造的最小生成树可能不唯一
1. Prim(普里姆)算法
算法思想
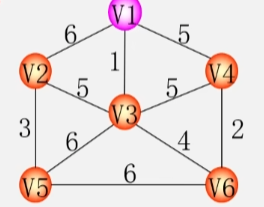
- 假设 N = (V,E) 是连通网,TE是 N 上最小生成树中边的集合。
- TE:在有 n 个顶点中的图中找到 n-1 条边,TE 里存着的就是这 n-1 条边,也就是最小生成树中所有的边。
- 初始令 U = {U0} (从某一个顶点开始构成最小生成树)(U0 ∈ V),令边集TE合为空 TE = { }。
- 这个 U0 就取 V1 来开始构成最小生成树。
- 采用 MST性质:那么 V1 就是 U 集合当中的一个顶点,其余顶点为 V-U 集合中的顶点。
- 在所有 u∈U,v∈V-U 的边 (u,v)∈E 中,找一条权值最小的边 (U0,V0)。
- 将(U0,V0) 这条边 并入边集合 TE,同时将这一条边相关联的顶点 V0 并入 U (放到最小生成树中)。
- 此时最小生成树上的顶点就有两个了。
- 剩下的 4 个顶点就是 V-U 集合中的顶点了。
- 接下来继续找已经在生成树上的点,和不在生成树上的点之间,找一条权值最小的边,显然就是 V3 - V6 之间的权值最小。
- 之后就是以此类推,从在树上的所有点和不在树上的所有点之间找一条权值最小的边。
- 将这条边以及这条边连接的点放入树中(边放入 TE ,点放入 U 中)。
- 重复上述操作直至 U=V(U集合包含所有的顶点) 为止,则 T = (V,TE) 为 N 的最小生成树。
2. Kruskal(克鲁斯卡尔)算法
- 之前说过后 Prim算法 和 Kruskal算法 都是使用的 MST 性质。
- MST 本质上就是贪心算法,只不过 Kruskal 算法更贪心而已。
算法思想
- 设连通网 N = (V,E),令最小生成树初始状态为只有 n 个顶点而无边的非连通图 T=(V,{ }),每个顶点自成一个连通分量
- 人话:一开始就直接把连通图上的所有顶点放到最小生成树集合中,但不放边进去。
- 在 E 中选取权值最小的边,若该边依附的顶点落在 T 中不同的连通分量撒花姑娘(即:不能形成环)。则将此边加入到 T 中;否则,舍去此边,选取下一天权值最小的边。
- 在连通图中找边的权值最小的边,但是每次找最小的比较麻烦,所以直接将所有的边按照权值排序,排序完之后直接从最小的边开始选。
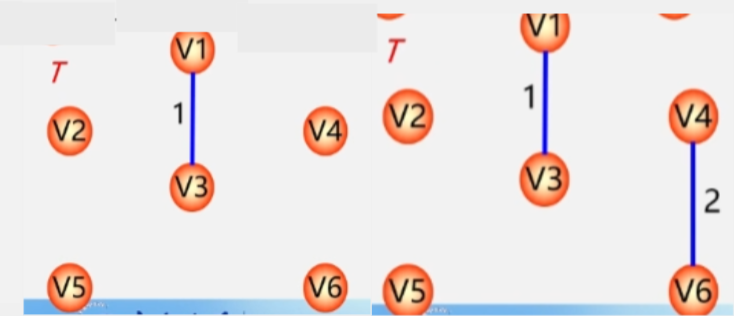
- 目前权值最小的是 V1 V3之间的边,将这条边加入生成树。
- 然后权值最小的变为 V6 V4 之间权值为 2 的边,将这条边加入生成树。
- 以此类推,直到 T 中所有顶点都在同一个连通分量上为止(选出了n-1条边为止)。
-
注意:当有多个权值相同的边时,不能选会让变成环的边,比如:就不能选V1和V4之间的边,否则直接变成环。
-
此时已经有了 n-1 条边了,最小生成树构造完成。
两种算法比较
6.6.2 最短路径
最短路径问题
典型用途:
- 交通网络的问题:从甲地到乙地之间是否有公路连通?
- 在有多条道路的情况下,那一条路最短?
交通网络用有权网来表示
- 顶点:表示地点。
- 弧:表示两个地点有路连通。
- 弧上的权值:表示两个地点之间的距离、交通费或路途中所花费的时间等。
如何能够使一个地点到另一个地点的运输时间最短或运费最省,这就是一个求两个地点之间的最短路径问题。
问题抽象:
- 在有向网中 A 点(起点)到达 B 点(终点)的多条路径中,寻找一条各边权值之和最小的路径,即最短路径。
- 最短路径与最小生成树不同,路径上不一定包含 n 个顶点,也不一定包含 n-1 条边。
第一类问题
- 求两点间最短路径
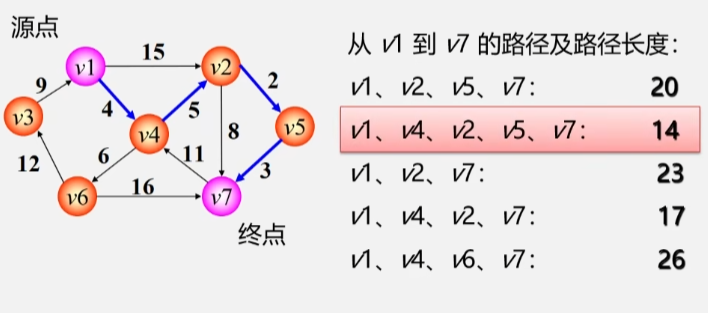
- 这类问题称作单源最短路径,使用==Dijkstra(迪杰斯特拉)==算法。
第二类问题
- 某源点到其他各点最短路径
- 这类问题称作所有顶点间的最短路径,使用Floyd(弗洛伊德) 算法。
1. Dijkstra(迪杰斯特拉)算法
算法实现
- 初始化:先找出从源点 V0 到各终点 Vk 的直达路径(V0,Vk),即通过一条弧到达的路径。
- 选择:从这些路径中找出一条路径长度最短的路径(V0,u)。
- 更新:然后对其余各条路径进行适当调整:
- 若在图中存在弧(u,Vk),且==(V0,u)+(u,Vk)<(V0,Vk)==,则用这条更短路径(V0,u,Vk)代替(V0,Vk)。
- 在调整后的各条路径中,再找长度最短的路径,依次类推。
迪杰斯特拉算法:按照路径长度递增次序产生最短路径。
-
把 V 分成两组:
- S:已求出最短路径的顶点的集合。
- T = V-S:尚未确定最短路径的顶点集合。
-
将 T 中顶点按最短路径递增到的次序加入到 S 中。
- 保证:从源点 V0 到 S 中各定点的最短路径长度都不大于从 V0 到 T 中任何顶点的最短路径长度。
- 每个顶点对应一个距离值:
- S 中顶点:从 V0 到此顶点的最短路径长度。
- T 中顶点:从 V0 到此顶点的只包括 S 中顶点作中间顶点的最短路径长度。
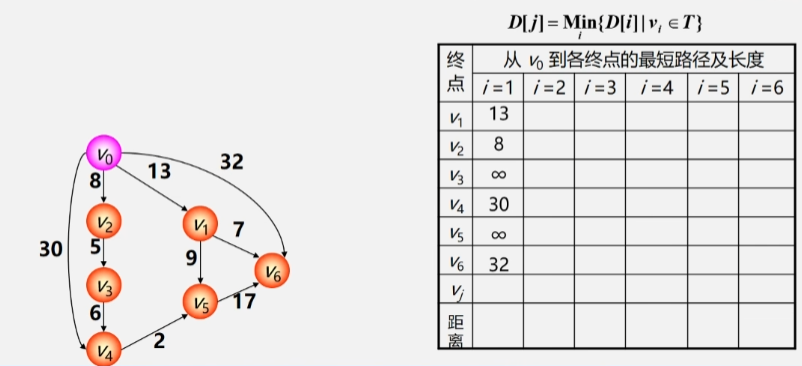
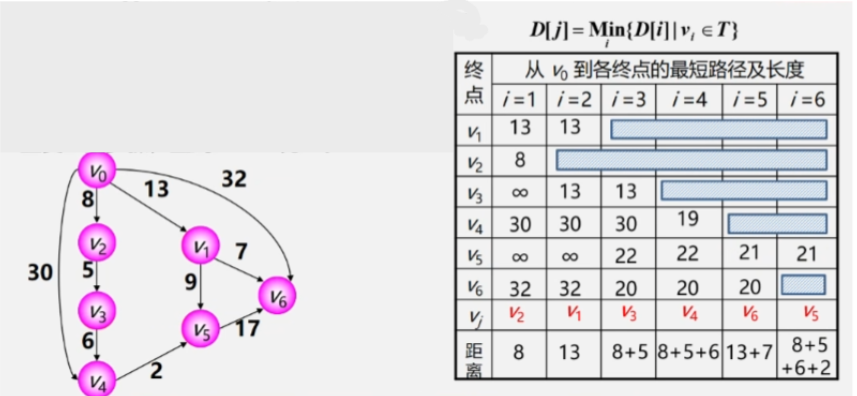
迪杰斯特拉算法步骤
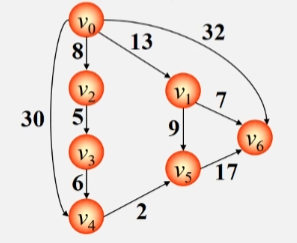
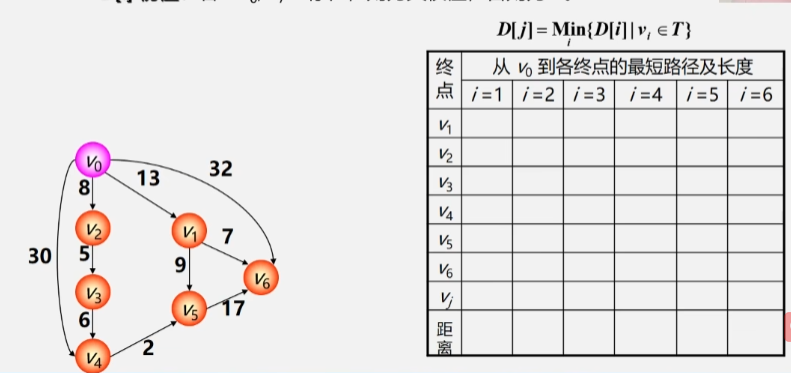
- 初始时令 S = {V0},T = {其余顶点}。
- T 中顶点对应的距离值用辅助数组 D 存放。
- D[i] 初值:若 <V0,Vi> 存在(两点间存在弧),则为其权值;否则为 ∞。
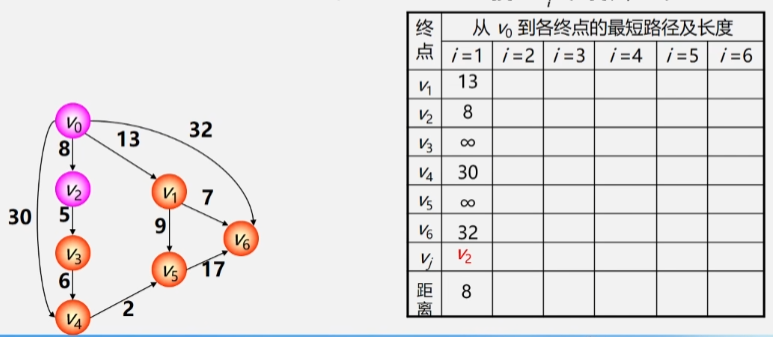
- 选择:从 T 中选取一个其距离值最小的顶点 Vj 加入 S。
- 接下来要在这里面找到权值最小的路径与 V0 连接的另一个顶点 V2 加入 Vj。
- 此时 V2 就加入了已经找到最短路径的顶点集合 S 中了,T 中少了个顶点。
-
更新:对 T 中顶点的距离值进行修改:若加进 Vj 作为中间顶点,从 Vo 到 Vi 的距离值比不加 Vj 的路径要短,则修改为此距离值。
- 人话:之后再看从 V0 直接出发到各个顶点的路径,以及 V0 经过 V2 再到其他顶点的路径。
- 看看到其余顶点之间的路径有没有减少,如果减少则更新成新的路径。
- V0经过V2到无法抵达V1,所以V0到V1之间的路径还是13 没有变化。
- V0到V2就不用看了,它已经找到最短路径了。再看从V0经过V2到V3之间的路径为13。最后V0到V4为30。
- V0到其余顶点之间即没有弧连着,也没有像V2这样的桥梁中转,所以全部为∞。
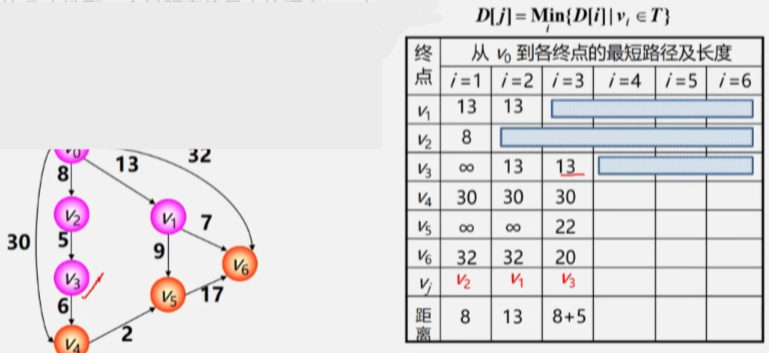
- 继续挑一个路径与V0之间路径最短的顶点加进 Vj(已找到最短路径的顶点集合)中,此时 V0-V1已经找到最短路径,不再看V1。
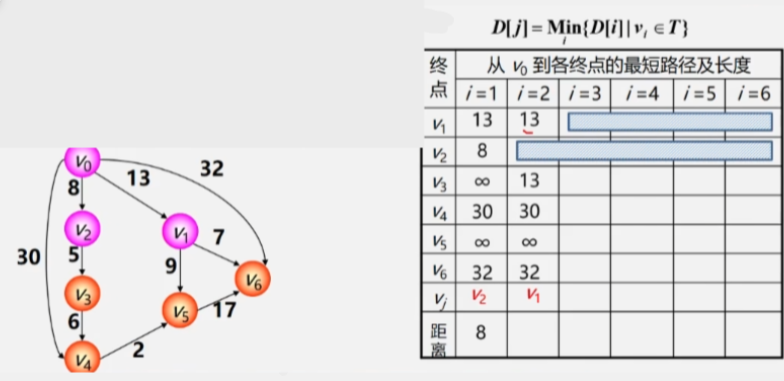
- 之后 V0 再以 V2、V1作为跳板跑到其他顶点,看看到其余顶点间的最短路径有没有变的更短。
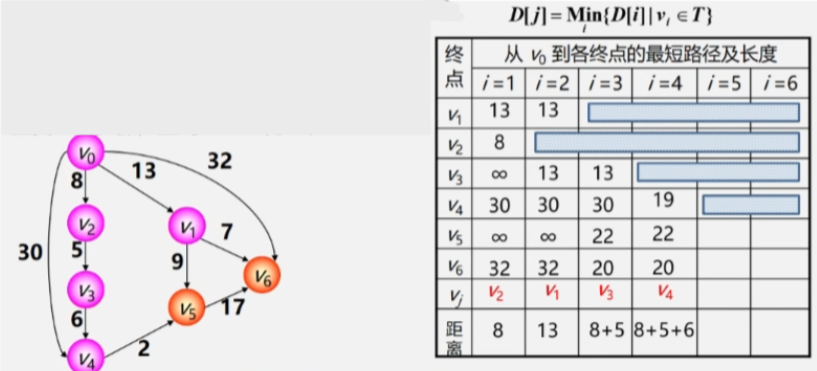
- 将 V3 加入最短路径顶点集,之后再以 V3 作为跳板收拾其他顶点。
- 之后就是依次类推不断更新最短路径,以及将 V0 与最短路径之间连着的顶点加进 Vj 。
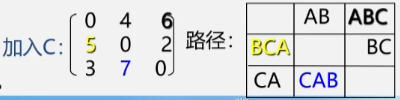
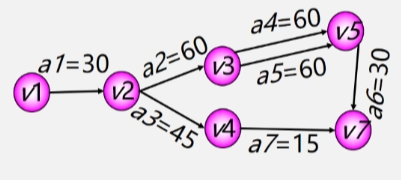
2. Floyd(弗洛伊德)算法
求所有顶点间的最短路径:
- 方法一:每次以一个顶点为源点,重复执行迪杰斯特拉算法 n 次。这个算法的时间复杂度是 O(n3)。
- 方法二:Floyd(弗洛伊德)算法,这个算法要简单很多,但是这个算法的时间复杂度任然是 O(n3)。
算法思想:
- 逐个顶点试探。
- 从 Vi 到 Vj 的所有可能存在的路径中。
- 选出一条长度最短的路径。
弗洛伊德算法步骤
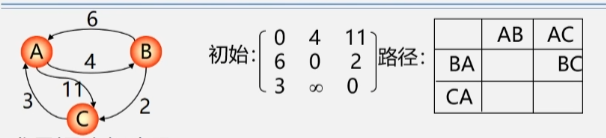
算法步骤
- 初始时设置一个 n 阶方阵:
- 令其对角线元素为 0(对角线元素都是到自身的路径,不考虑自己和自己之间的路)。
- 两点之间若存在弧 <Vi,Vj>,则其对应元素为该弧的权值;否则为 ∞。
- 逐步试着在原直接路径中增加中间顶点:
- 若加入中间顶点后路径变短,则修改之,反之,维持原值。
- 直到所有顶点试探完毕,算法结束。
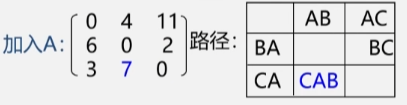
- 加入顶点 A 之后,令 C 到 B 之间有了条路,对于其余顶点之间的路径并没有影响。
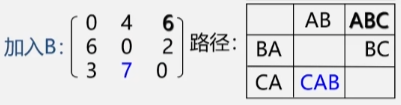
- 加入顶点 B 之后,令 A 到 C 之间的最短路径变为了 ABC 这条路径长度为 6 的路径,将最短路径修改为这这个,对其余顶点间的路径长度无影响。
- 加入顶点 C 之后,令 B 到 A 之间的最短路径从 BA 的 6 变为了 BCA 的 5,将最短路径修改成这个。
有向无环图及其应用
有向无环图:无环的有向图,简称 DAG 图。
- 有向无环图常用来描述一个工程或系统的进行过程。(通常把计划、施工、生成、程序流程当成是一个工程)
- 一个工程可以分为若干个子工程,只要完成了这些子工程(活动),就可以使得整个工程的完成。
如何表示这些子工程?
- AOV 网:拓扑排序
- 用一个有向图表示一个工程的各个子工程及其相互制约的关系,其中以顶点表示活动,以弧表示活动之间的优先制约关系,称这种有向图为顶点表示活动的网,简称 AOV 网(Activity On Vertex network)。
- AOE 网:关键路径
- 用一个有向图表示一个工程的各个子工程及其相互制约的关系,以弧表示活动,以顶点表示活动的开始或结束事件,称这种有向图为边表示活动的网,简称 AOE 网(Activity On Edge)
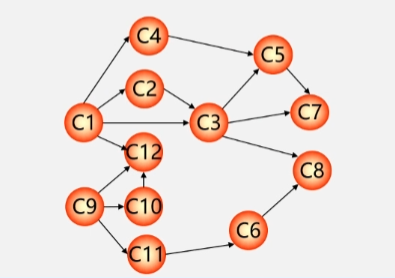
6.6.3 拓扑排序
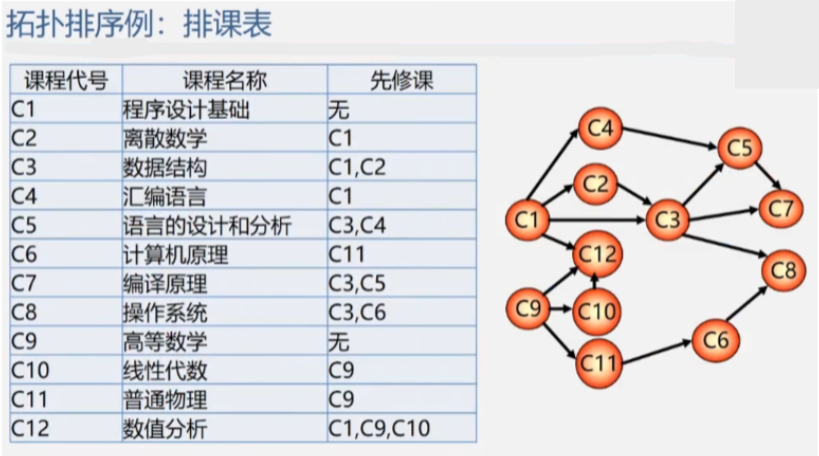
假设现在要安排一份课程表:
-
想要学习数据结构这门课的话,事先得先学习离散设计和程序设计基础,所以数据结构的先修课就是 C1、C2这两门课。
-
再如 C9 的高等数学,他没有先修课(前趋),但是从图中看,C12、C10以及C11都需要先学习过 C9 的课,所以 C9 可以当成是这三门课的直接前趋。
-
同样的,只有学完了 C9 的数据结构之后,才能学习它的后继课程。
-
既然要开设这么些课程,但是有着明显前趋后继关系的课程又不能同时进行,怎么才能将这些课排在各个学期,而且还满足表中的先后关系,这个时候就要用到俺们的拓扑排序了。
在有向网中:用顶点表示要上的课程,用带方向的弧来表示这些课程之间的先后关系
AOV 网的特点:
- 若 从 i 到 j 有一条有向路径,则 i 是 j 的前趋;j 是 i 的后继。
- 如:从 C1 到 C5 之间有条有向路径,则称 C1 为 C5 的前趋;C5 为 C1 的后继。
- 若 < i , j > 是网中的有向边,则 i 是 j 的直接前趋;j是 i 的直接后继。
- 如:C1 到 C3 之间有一条边,则称 C1 为 C3 的直接路径;C3 为 C1 的直接后继。
- AOV 网中不允许有回路,因为如果有回路存在,则表明某项活动是以自己为先决条件,显然这样不行。
- 如:假设必须学完 C2 才能学习 C1 的课程,C1 学完之后才能学 C3,C3 学完了才能学 C2。那这就糊涂了,该先学那门课捏?
- 问题:如何判别 AOV 网中是否存在回路?
拓扑排序的方法
- 在 AOV 网没有回路的情况下,我们将全部活动排列成一个线性序列,使得 AOV 网中有弧 < i , j > 存在,则在这个序列中,i 一定排在 j 的前面,具有这种性质的线性序列称为拓扑有序序列,相应的拓扑有序排序的算法称为拓扑排序。
首先先把这个 AOV 网构造出来,用顶点来表示学习的课程,用顶点之间的有向弧来表示学习的顺序。
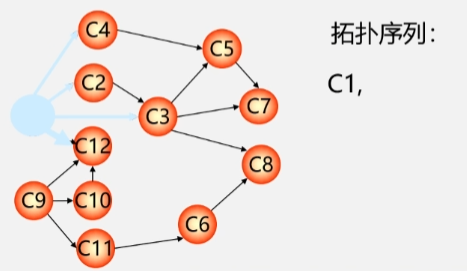
拓扑排序过程
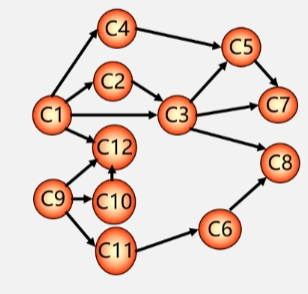
- 在有向图中选一个没有前趋的顶点且输出它。
- 如:一开始在图中发现只有C1和C9没有前趋,选一个序号最小的 C1 出去。
- 在图中删除该顶点,以及所有从该顶点发射出去的弧。
- 将 C1 以及它所发射出去的四条弧从图中删除。
- 重复(1)和(2),直到不存在没有前趋的顶点。
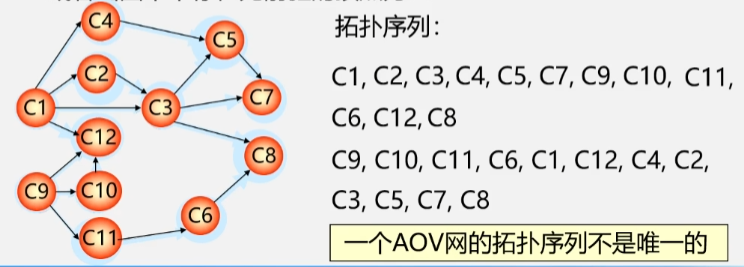
- 拓扑序列的先后顺序不唯一。
- 但是如果在图中某个顶点是另一个顶点的前趋,那么在线性序列中该顶点也必须是另一个顶点的前趋。
- 如:顶点 C3 是 C8 的前趋,那么在拓扑序列中,C3 的位置也必须在 C8 前面。
- 若此时输出的顶点数小于有向图中的顶点数,则说明有向图中存在环,返之说明输出的顶点序列为一个拓扑序列。
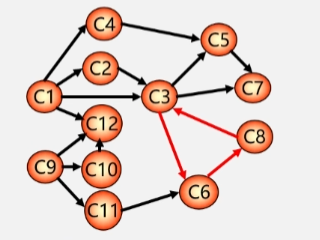
检测 AOV 网中是否存在环
- 对有向图构造其顶点的拓扑有序序列.
- 若网中所有顶点都在它的拓扑有序序列中,则该 AOV 网必定不存在环。
简单来说如果一个顶点有环的话,即便删掉他的前驱和相关约束关系,他自己或者它后继在约束它本身,所以他不可能变成那种没有前驱的结点被输出,这时拓扑序列的顶点个数必定不等于总顶点个数,可能有人会说,那为啥后继对它的约束不能被删除呢,那是因为后继的前驱是当前结点,当当前结点没被删除时,后继怎么可能删除呢。
在这三个顶点中找不到没有前趋的顶点,这几个顶点没法加到拓扑序列汇总。
6.6.4 关键路径
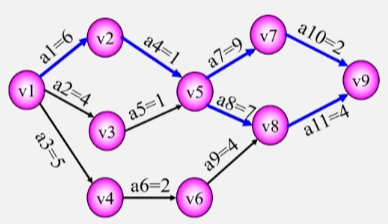
用AOE网表示工程计划
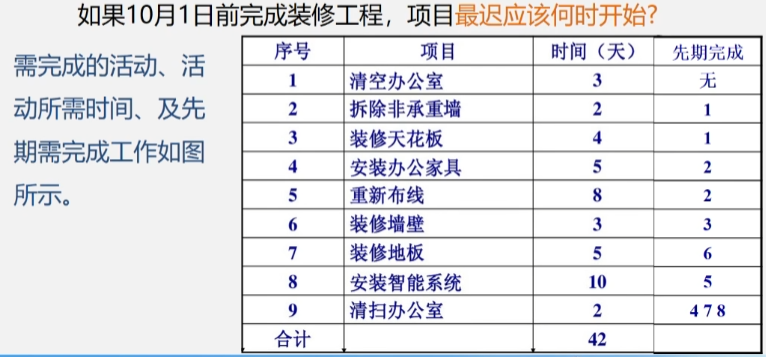
【例1】:某项目的任务是对A公司的办公室重新进行装修
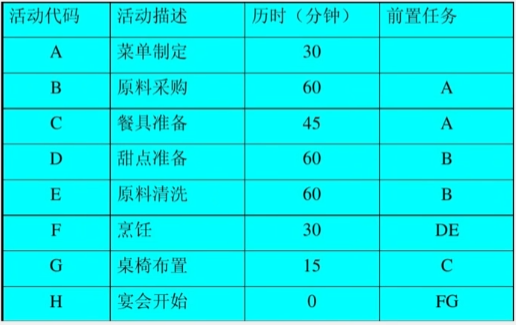
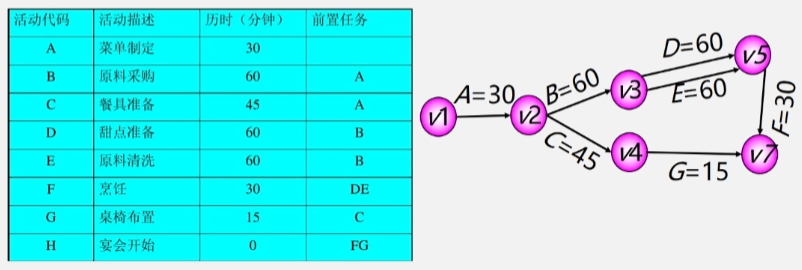
【例2】:准备一个小型家庭宴会,晚上六点宴会开始,最迟机电开始准备?压缩哪项活动时间可以让总时间减少?
- 把工程计划表示为边表示活动的网络,即 AOE 网,用顶点表示事件,弧表示活动,弧的权表示互动持续时间。
- 事件(顶点):表示在它之前的活动已经完成,在它之后的活动可以开始。
- 如:顶点 V2 表示 A 活动结束,BC 活动可以开始,顶点 V3 表示 活动 B 结束,DE 活动可以开始。
求解关键路径
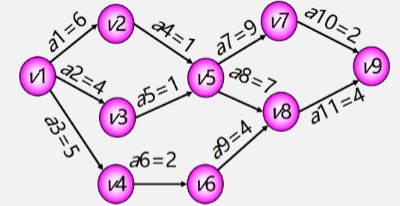
例:设一个工程有 11 个活动,9 个事件。
- 事件 V1:表示整个工程开始(源点:入度为 0 的顶点)。
- 事件 V9:表示整个工程结束(汇点:出度为 0 的顶点)。
有了这样一个AOE网后,现在有两个问题:
- 完成整项工程至少需要多少时间?
- 关键路径的长度,就是整个工程至少需要的时间。
- 哪些活动是影响工程进度的关键?
- 关键路径上的这些活动就是影响工程进度的关键。
- 关键路径:从源点到汇点路径长度最长的路径。
- 路径长度:路径上各活动持续时间(权值)之和。
道理很简单,就是几个人同时到一个地方集合,离得近的到得早,离得远的到得晚,但只有最晚到的人到了,大家才算凑到一块了。
确定关键路径
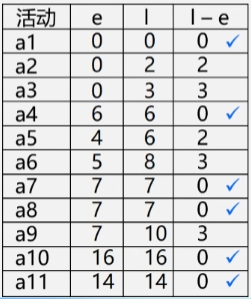
为了确定关键路径,需要定义 4 个描述量:
假设所有活动全部完成需要消耗 180 分钟
- ve(vj):关于顶点的,表示事件 vj 的最早发生时间。
- 如:V2 事件,表示 a1 最早可以什么时候完成,和 a2 最早什么时候可以开始的时间。
- ve(v1) = 0(事件 v1 不需要等待时间),ve(v2) = 30(事件 v2 连着的活动需要等 a1 的 30 完成了之后才能开始)
- vl(vj):关于顶点的,表示事件 vj 的最迟发生时间。
- 如:假设所有活动要消耗 180 分钟,活动 a7 需要15分钟,V4 的 a3 最晚要在第 165 分钟的时候结束,活动 a7 最迟要在第 165 分钟开始。
- 例:vl(v4) = 165
- e(i):表示活动 ai 的最早开始时间
- 例:e(a3) = 30,活动 a3 最早能在第30分钟的时候开始。
- l(i):表示活动 ai 的最晚开始时间。
- 例:l(a3) = 120,因为180分钟至少要预留15分钟给a7,所以 a3 至少要在这 165 分钟内完成,a3要花费45分钟,所以活动 a3 最迟要在第 120 分钟开始。
- l(i) - e(i):表示完成活动 ai 的时间余量
- 例:l(3) - e(3) = 90,活动 a3 在这 90 分钟内什么时候开始都不会影响进度。
- 关键活动:没有时间余量的活动,关键路径上的路径,即 l(i) = e(i)(即 l(i) - e(i) = 0)的活动。
- 由若干个关键活动所组成的路径就是关键路径。
如何找l(i) = e(i) 的关键活动?
设活动 ai 用弧 <j , k> 表示,其持续时间记为:Wj,k,则有:
- e(i) = ve(j)
- l(i) = vl(k) - Wj,k
如何求 ve(j) 和 vl(j)?
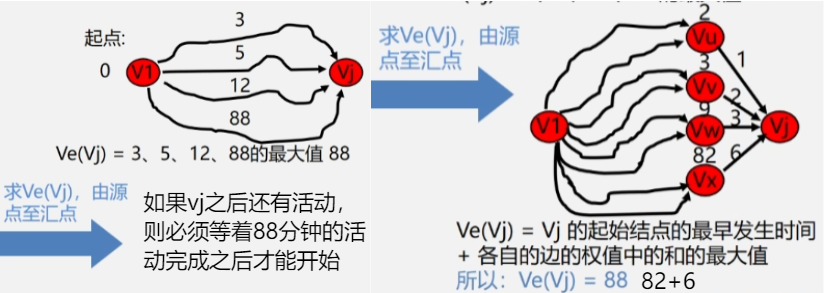
- 求最早发生时间:从 ve(1) = 0开始向前递推
- ve(j) = Max{ve(i) + Wi,j},< i,j > ∈ T,2 <= j <= n。其中 T 是所有以 j 为头的弧的集合。
- 从源点到某个顶点的全部路径中,选择路径长度(权值和)最大的那条路。
- 例:开始刷牙到结束刷牙,根据你出门时间决定你最晚刷牙时间,根据你起床决定最早刷牙时间。
- 求最晚发生时间:从 vl(n) = ve(n) 开始向后递推。
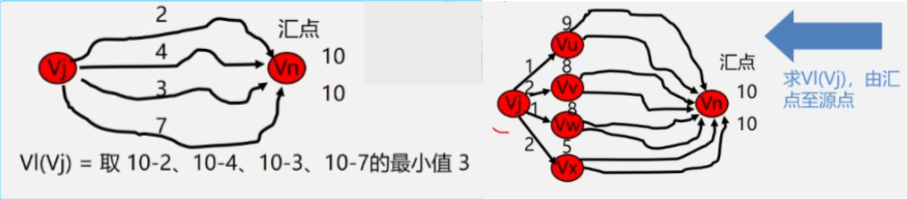
- vl(i) = Min{vl(j) - Wi,j},< i,j > ∈ S,1 <= i <= n-1。其中 S 是所有以 i 为尾的弧的集合。
- Vi 顶点后继的那个顶点Vj的最迟发生时间减去Vi与Vj之间弧的权值。
顶点 vj 的最早发生时间
顶点 vj 的最迟结束时间
- 后面的顶点减去前面的顶点之间的弧的权值,取差的最小值
求关键路径步骤
- 求 ve(i)、vl(j):事件的最早、晚发生时间
- 求 e(i)、l(i):活动的最早、晚开始时间
- e(i) = ve(j):活动的最早发生时间 = 对应顶点事件的最晚发生时间
- l(i) = vl(k) - Wj,k:对应顶点事件最迟发生时间减去活动的持续时间。
- 如:活动 a1 的最迟发生时间就是 V2 的六分钟减去 a1 持续的时间 6 分钟 = 0。也就是说活动 a1 现在立马就得开始。
- 计算 l(i) - e(i):
- 差值时间为 0 的活动是关键活动。
- 由若干个关键活动所组成的路径就是关键路径
- 所以关键路径就是 a1 a4 a7 a8 a10 a11