由数据范围反推算法复杂度以及算法内容 - AcWing
常用代码模板4——数学知识 - AcWing
基本思想：
这里我们了解一下欧拉函数是什么以及用筛法求欧拉函数，我们先给出欧拉函数的定义：
然后我们了解一下互质的概念，只要两数的公因数只有1时，就说这两个数是互质的。
φ(N)的公式的证明会用到后续学到的容斥原理，这里就直接用容斥原理（思想大致是 在计数时，先不考虑重叠的情况，把包含于某内容中的所有对象的数目先计算出来，然后再把计数时重复计算的数目排斥出去，使得计算的结果既无遗漏又无重复）来证明
首先我们减去所有质因子的倍数，然后我们会发先现如果一个数同时是pi和pj的倍数，那么它会被减去两次，所以我们需要加起来，假如一个数是pi，pj，pk的倍数，它先被减去三次，然后加上三次，所以还需要减去一次，依次类推，奇数倍的需要减去，偶数倍的需要加上，这也就是我们的容斥原理的思想，我们将式子整理后就会得到我们的欧拉函数的公式，即证明。
873. 欧拉函数 - AcWing题库
给定 n 个正整数 ai，请你求出每个数的欧拉函数。
输入格式
第一行包含整数 n。
接下来 n 行，每行包含一个正整数 ai。
输出格式
输出共 n 行，每行输出一个正整数 ai 的欧拉函数。
数据范围
1≤n≤100,
1≤ai≤2×1e9
输入样例：
3
3
6
8
输出样例：
2
2
4
//只要两数的 公因数 只有1时，就说两数是互质数 #include<iostream> using namespace std; int main() { int n; cin>>n; while(n--) { int x; cin >> x; int res = x; for(int i = 2; i <= x / i; i++) { if(x % i == 0) { res = res / i * (i - 1); // 等价于res = res * (1 - 1 / a) while(x % i == 0) x /= i; } } if(x > 1) res = res / x * (x - 1); cout << res << endl; } return 0; }
筛法求欧拉函数，通过线性筛法来降低我们的时间复杂度，从O(N*根号N)降低到O(N)
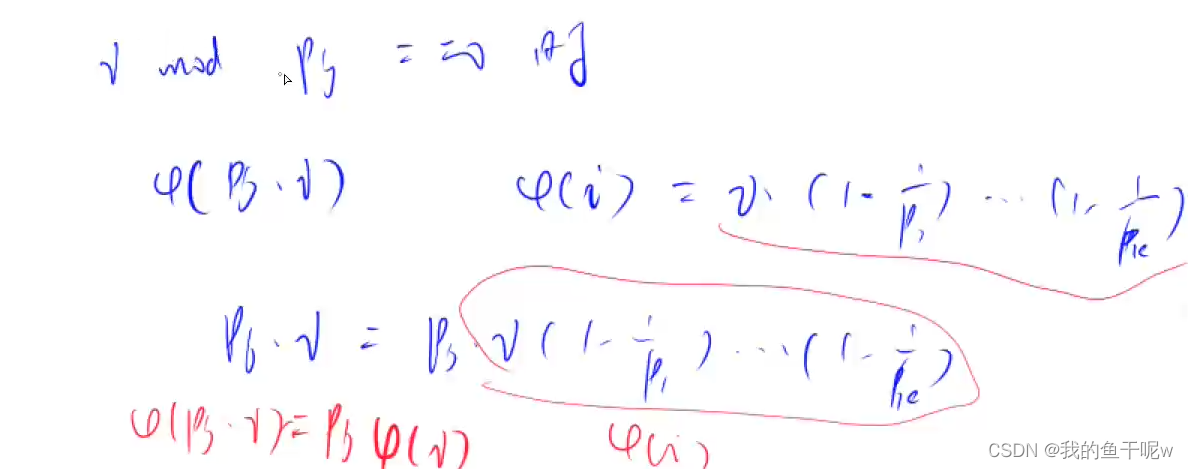
在这里我们先将线性筛法的模版写出，线性筛法在数论中经常会用到，模版要牢记，然后我们来推出欧拉函数公式怎么转化，我们分成三种情况：
第一种，即特殊情况，当一个数i为质数时，那么与他互质的数就是i - 1个；
第二种，当i % pj == 0 时，phi[i] 与phi[pj * i] 只多了一个pj，因为pj是i的质因子,在phi[i]中已经减去了一个1 - 1 / pj，而且欧拉函数的公式中不用考虑质因子的指数，比较一下可以发现phi[pj * i] 比phi[i]多乘了一个pj，所以可以推出phi[pj * i] = pj * phi[i]
第三种，当i % pj != 0 时，因为pj不是i的质因子，在phi[i]中并未减去1 - 1 / pj ，所以此时phi[pj * i]应该等于phi[i] * pj * (1 - 1 / pj) ，即phi[pj * i] = phi[i] * (pj - 1)
874. 筛法求欧拉函数 - AcWing题库
给定一个正整数 n，求 1∼n 中每个数的欧拉函数之和。
输入格式
共一行，包含一个整数 n。
输出格式
共一行，包含一个整数，表示 1∼n 中每个数的欧拉函数之和。
数据范围
1≤n≤1e6
输入样例：
6
输出样例：
12#include<iostream> using namespace std; typedef long long LL; const int N = 1000010; int primes[N], cnt; int phi[N]; bool st[N]; LL get_eulers(int n) { for(int i = 2; i <= n; i++) { if(!st[i]) { primes[cnt++] = i; phi[i] = i - 1;//特殊情况 当一个数为质数时，那么与他互质的数就是i - 1 } for(int j = 0; primes[j] <= n / i; j++) { st[primes[j] * i] = true; if(i % primes[j] == 0) { phi[primes[j] * i] = primes[j] * phi[i]; //第一种情况 当i % pj == 0 //phi[i] 与phi[pj * i] 只多了一个pj //因为pj是i的质因子,在phi[i]中已经减去了一个1 - 1 / pj //而且欧拉函数的公式中不用考虑质因子的指数 //所以可以推出phi[pj * i] = pj * phi[i] break; } phi[primes[j] * i] = phi[i] * (primes[j] - 1); //第二种情况 当i % pj != 0 //因为pj不是i的质因子 //在phi[i]中并未减去1 - 1 / pj //所以此时phi[pj * i]应该等于phi[i] * pj * (1 - 1 / pj) //即phi[pj * i] = phi[i] * (pj - 1) } } } int main() { int n; cin >> n; cout << get_eulers(n); return 0; }
