原题:
You are given a string s, consisting of lowercase Latin letters.
You are asked q queries about it: given another string t, consisting of lowercase Latin letters, perform the following steps:
concatenate s and t;
calculate the prefix function of the resulting string s+t;
print the values of the prefix function on positions |s|+1,|s|+2,…,|s|+|t| (|s| and |t| denote the lengths of strings s and t, respectively);
revert the string back to s.
The prefix function of a string a is a sequence p1,p2,…,p|a|, where pi is the maximum value of k such that k<i and a[1…k]=a[i−k+1…i] (a[l…r] denotes a contiguous substring of a string a from a position l to a position r, inclusive). In other words, it’s the longest proper prefix of the string a[1…i] that is equal to its suffix of the same length.
Input
The first line contains a non-empty string s (1≤|s|≤10^6), consisting of lowercase Latin letters.
The second line contains a single integer q (1≤q≤10^5) — the number of queries.
Each of the next q lines contains a query: a non-empty string t (1≤|t|≤10), consisting of lowercase Latin letters.
Output
For each query, print the values of the prefix function of a string s+t on positions |s|+1,|s|+2,…,|s|+|t|.
Examples
input
aba
6
caba
aba
bababa
aaaa
b
forces
output
0 1 2 3
1 2 3
2 3 4 5 6 7
1 1 1 1
2
0 0 0 0 0 0
input
aacba
4
aaca
cbbb
aab
ccaca
output
2 2 3 1
0 0 0 0
2 2 0
0 0 1 0 1
中文:
给你个字符串s,然后给你q个不同的字符串t。每次构造一个新的字符串s+t,记|s|为字符串s长度,|t|为字符串t的长度,现在要每次计算出|s| + 1到 |s| + |t|的next值(就是kmp的next数组)
代码:
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e6 + 5;
string s, t;
int jump[maxn][26];
int Next[maxn];
int q;
void solve()
{
cin>>s;
int n=s.size();
s=' '+s;
for (int i=1,j=0;i<=n;i++)
{
if (i!=1) {
while (j&&s[j+1]!=s[i]) {
j=Next[j];
}
if (s[j+1]==s[i]) {
j++;
}
Next[i] = j;
}
for (int k=0;k<26;k++) {
if (i!=n&&s[i+1]==char('a'+k)) {
jump[i][k]=i;
}
else {
jump[i][k]=jump[Next[i]][k];
}
}
}
/*
cout << "next val = " << endl;
for (int i = 1; i <= n; i++) {
cout << Next[i] << " ";
}
cout << endl;
for (int i = 1; i <= n; i++) {
for (int j = 0; j < 26; j++) {
if (jump[i][j] == 0) {
continue;
}
cout << "jump[" << i <<"][" << char(j+'a') <<"] = " << jump[i][j] << endl;
}
cout << endl;
}
cout << endl;
*/
cin>>q;
while (q--)
{
cin>>t;
int m=t.size();
int j=Next[n];
s+=t;
for (int i=n+1,j=Next[n];i<=n+m;i++) {
while (j&&s[j+1]!=s[i]) {
if (j<=n) {
// cout << "j = " << j << " dp = " << jump[j][st[i] - 'a'] <<" " << (st[j+1] == st[i]) << endl;
j=jump[j][s[i]-'a'];
break;
}
j=Next[j];
}
if (s[j+1]==s[i]) {
j++;
}
Next[i] = j;
cout<<Next[i]<<" ";
}
cout<<endl;
while (m--) {
s.pop_back();
}
}
}
int main()
{
ios::sync_with_stdio(false);
int t=1;
while (t--) {
solve();
}
return 0;
}
思路:
肯定能想到是kmp算法,因为要计算前缀数组,如果暴力求解会超时,这里需要使用kmp自动机,如果有ac自动机的基础,则很容易想到。
考虑如下字符串
s = “ababcabaa”
t = "baba
那么s+t = “ababcabaababa”
计算出字符串s的前缀数组为:
1 2 3 4 5 6 7 8 9 |
------------------------- |
a b a b c a b a a | b a b a
0 0 1 2 0 1 2 3 1 |
如果使用原始kmp算法直接计算新拼接的字符串部分的next值会超时。
这里需要使用kmp自动机的概念,以上面的字符串为例
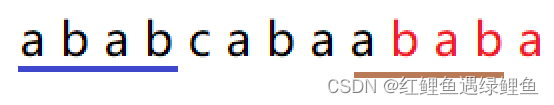
如上图,前缀abab与原始字符串最后一个字符串与新添加的后缀可以完全匹配上,但是到了前缀第5个字符串与后缀第5个字符分别是’c’和’a’不匹配。这时观察原始字符串前缀中abab这个子串,如果与其匹配的字符串的下一个字符串是c,那么当前的状态就应该返回4,即
jump [“abab”][‘c’] = 4,即得到"abab"最后一个一个’b’的位置。如果是遇到其它字符,则需要根据next数组,找到可以匹配的最长前缀的位置,比如jump[“abab”][‘a’] = ? ,由于next[“abab”] = 2,表示子串“abab"的前缀和后缀可以匹配上两个,即”ab",正巧前缀的“ab"下一个字符是’a’,那么jump[“abab”][‘a’] = 2,即表示如果"abab"匹配上了,下一个字符遇到的不是c,而是a的情况下,可以向前查找到的可匹配状态为2。
有了上面的jump数组,在计算新添加的字符串数组的时候,就可以利用jump信息,在新添加的字符与前缀字符未匹配上的时候,应该与前缀的某一个子状态可以匹配上。
ps:此题目也可以使用离线方法完成,将所有查询的字符串搜集起来并排序,找到公共前缀再进行计算,这样可以明显减少匹配次数。