光流估计（一）光流的简介与操作

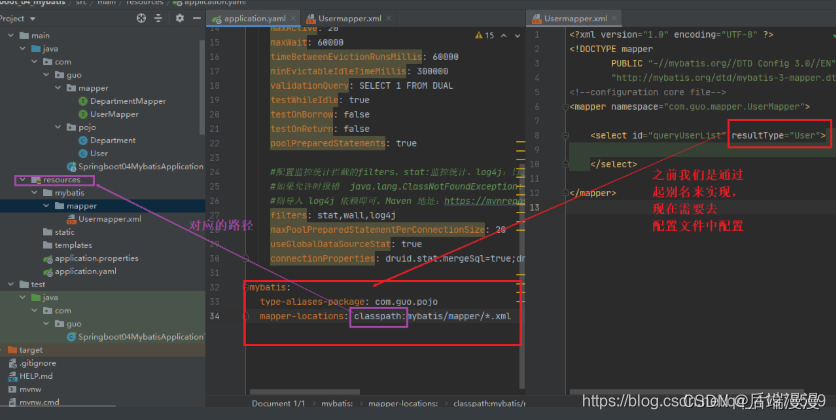
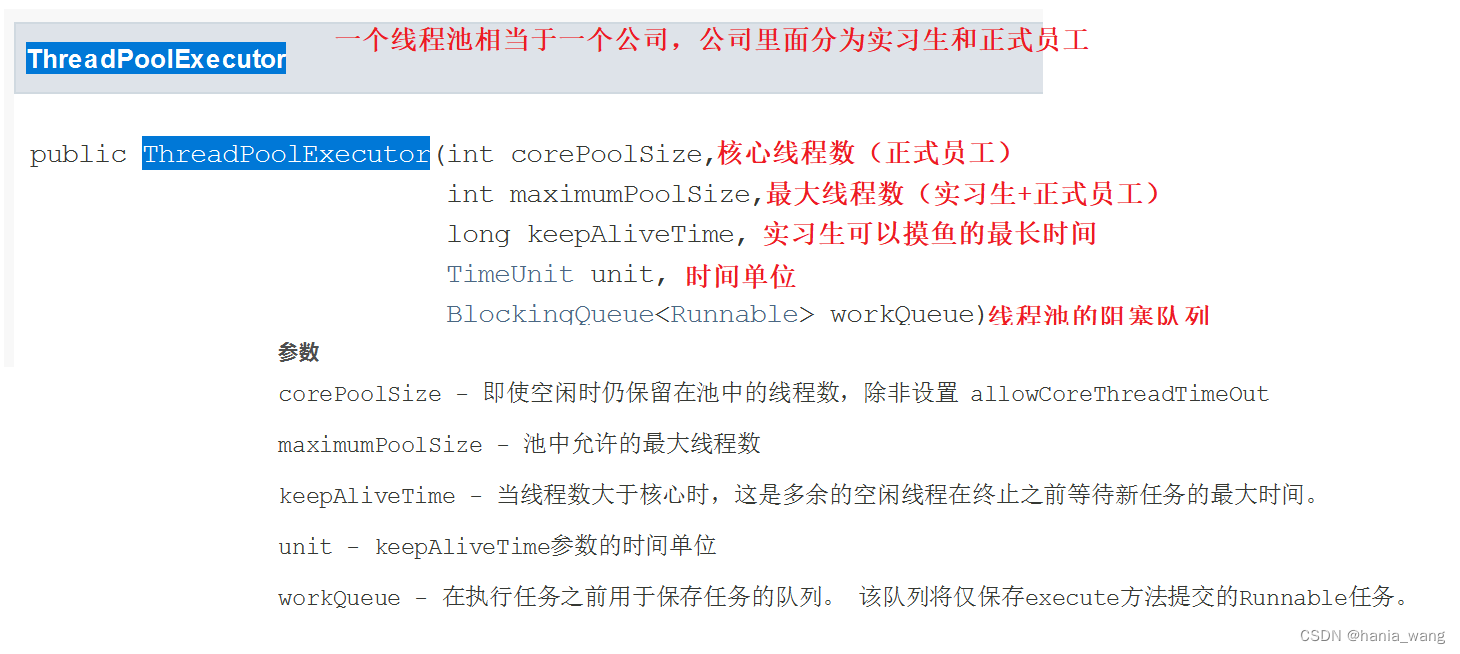
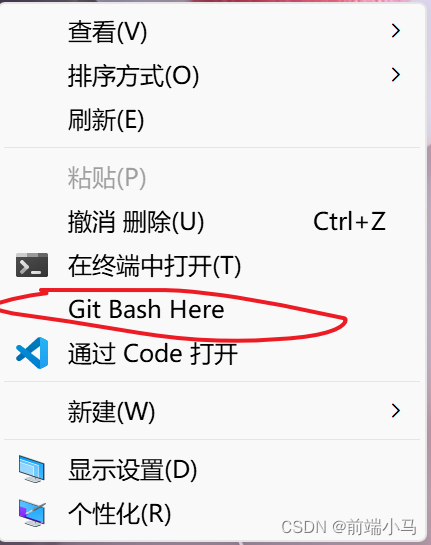
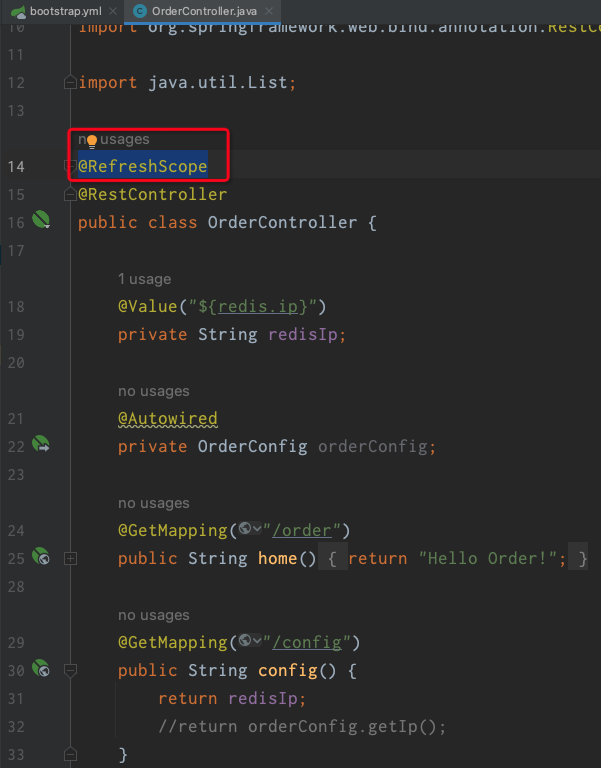
今天是大年29，明天要贴春联了！算是在年前赶出来一篇文章发（太长时间没发东西了O。o），也算是自己在光流估计深度学习部分研究的开始~ 明年开学就是研二下学期了，时间过得飞快，毕设、实习、工作等事情堆在面前像一座大山，希望明年一切顺利！我阿，只想做个平凡、普通、快乐的人，好难好难… …

一.光流的基本概念

1.光流与光流场

（1）光流

光流是空间运动物体在观察成像平面上的像素运动的瞬时速度，也有人将二维平面图像内特定像素点的灰度/亮度的瞬时变化率定义为光流（Optical flow can also be defined as the distribution of apparent velocities of movement of brightness pattern in an image.），当时间间隔很小时（比如视频的连续前后两帧之间）也等同于空间点在成像平面内投影点的位移。一般而言，光流是由于场景中前景目标本身的移动、相机的运动，或者两者的共同运动导致发生了相对运动所产生的。

通俗点来说，当人的眼睛观察运动物体时，物体的景象在人眼的视网膜上形成一系列连续变化的图像，这一系列连续变化的信息不断“流过”视网膜（即图像平面），形成了一连串图像亮度/灰度模式的运动，好像一种光的“流”，故称之为光流。也可以理解为图像中像素强度的流动。光流表达了图像的变化，由于它包含了目标运动的信息，因此可被观察者用来确定目标的运动情况。

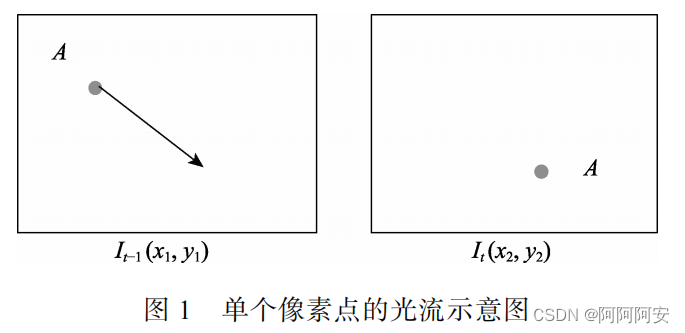
图像X（t-1帧）和图像Y（t帧）一般为视频流中相邻的两帧，某一像素点A在图像X中位置为 $x_1,y_1)$ ，经过运动在图像Y中位置为 $x_2,y_2)$ ，则这一像素点A的光流可计算为 $u_x,u_y) = (x_2,y_2) - (x_1,y_1)$ ，向量 $u_x,u_y)$ 就是该像素点产生的光流，其包含x方向和y方向的运动，光流的值是亚像素的浮点数值。如下图1所示，左图中的A点运动到右图, 箭头表示的是相邻两帧间A点的光流矢量。
在这里插入图片描述

（2）光流场

一系列像素点光流矢量的集合就形成了光流场。 光流场指图像中一系列像素点构成的一种二维(2D)瞬时速度场，其中的二维速度矢量是目标物体中可见点的三维速度矢量在成像表面的投影，一般来说三维运动场与通过投影形成在二维图像上的光流场相对应。
在这里插入图片描述

2.光流法与运动场

（1）运动场

运动场其实就是物体在三维真实世界中的运动，一系列的运动矢量构成了运动场，运动场可以用来描述物体的真实运动状态。空间中的运动场投影到二维图像平面（人的眼睛或者摄像头）上就表示为光流场（optical flow field），运动场和光流场的关系如下图所示。
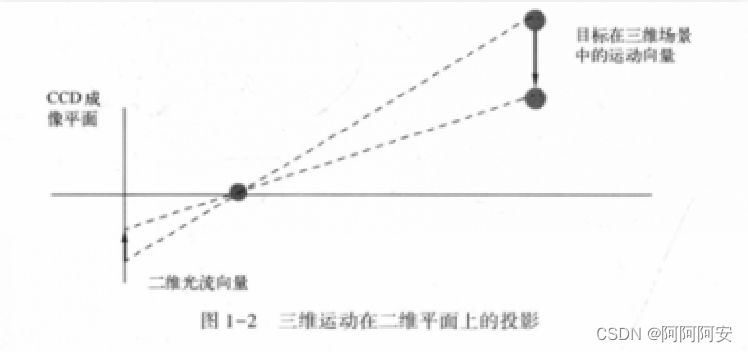
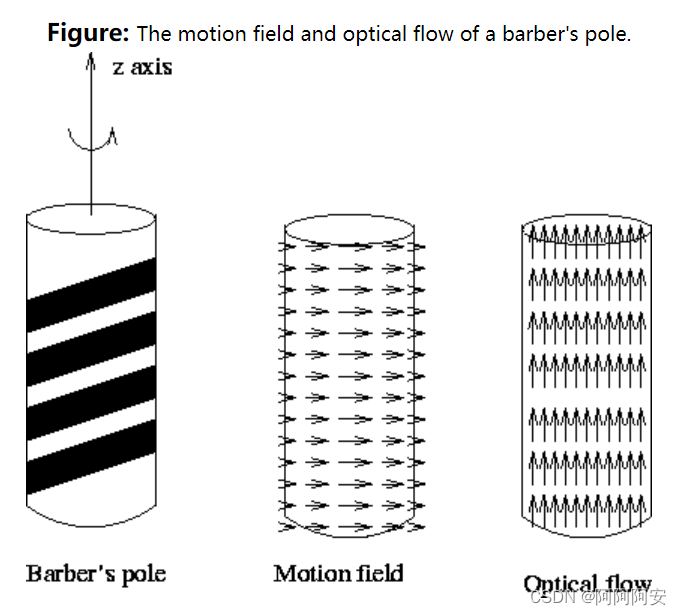
在这里插入图片描述

由上述可知光流矢量和运动矢量之间的联系十分密切，但二者并不是完全一致的，或者说运动场和其光流场之间不一定是完全对应的。因为，光流的产生是由于物体与相机之间出现了相对运动，而这个相对运动并不完全等同于真实运动状态。在生活中有一个常见的例子：理发店的经常用旋转的招牌来吸引顾客（如下图所示），这时从光流场的角度来看，招牌是向上旋转运动的；但是从运动场的角度来看，招牌其实是水平运动的。所以，光流场并不严格等同于其运动场，但这种情况是不常见的，在大多数情况下二者的表现是一致的，之后我们将假设光流场对应于运动场，这也就为我们将其运用到与运动矢量有关的问题中提供了可能。
在这里插入图片描述

（2）光流法

由于直接计算和分析三维空间中的运动场十分困难，而运动场与通过投影形成在二维图像上的光流场相对应，并且光流本质上是三维场景的物体运动投影到二维图像平面表现的像素点亮度变化，其不仅包含了被观察物体的运动信息，而且还包含了有关景物三维结构的丰富信息等。因此可以通过光流分析来对运动物体进行分析，光流法便应运而生并且成为计算机视觉中对运动目标进行分析的重要工具。

光流法是利用图像序列中像素在时间域上的变化以及相邻帧之间的相关性来找到上一帧跟当前帧之间存在的对应关系，从而计算出相邻帧之间物体的运动信息的一种方法，即从二维图像数据中估计物体的真实运动状态（光流场=>运动场）的方法。研究光流场的目的就是为了从序列图像中近似计算不能直接得到的运动场，根据图像中像素点的灰度值强度变化估计出物体移动的速度与方向。在一般理想情况下，光流场应对应于运动场。

3.稀疏光流与稠密光流

光流计算的理想输出是两帧图像中每个像素的速度的估计关联，或者等效的，一幅图像中每个像素的位移矢量，指示该像素在另一幅图像中的相对位置，如果图像中的每个像素都采用这种方法通常称为“稠密光流”；如果仅仅只跟踪图像中某些点的子集，则称为“稀疏光流”。

（1）稠密光流

稠密光流是一种针对图像或指定的一片区域进行逐点匹配计算的光流计算方法，它计算图像上所有的点的偏移量，从而形成一个稠密的光流场。通过这个稠密的光流场，可以进行像素级别的图像配准。由于光流矢量稠密，所以其配准后的效果明显优于稀疏光流配准的效果。但其副作用也比较明显，因要计算每个像素的偏移量，其计算量也明显较大，时效性较差。

（2）稀疏光流

稀疏光流并不对图像的每个像素点进行逐点计算，它通常需要指定一组点进行跟踪，这组点最好具有某种明显的特性，例如Harris角点等，跟踪才会相对稳定和可靠。稀疏跟踪的计算开销比稠密跟踪小得多。
在这里插入图片描述

4.光流估计

光流估计是用于在两帧图像之间建立/计算光流场的方法。常见的光流估计方法有基于梯度的方法、基于匹配的方法、基于深度学习的方法、基于能量的方法等，在后面的学习中我们会以基于深度学习的方法为主进行研究。由上述介绍可知，光流估计的核心问题即如何匹配两张图片的对应像素点，从而计算相应的光流矢量。
在这里插入图片描述

二.光流的表示和可视化

1.光流表示方法

光流估计的结果为原图像大小相等的双通道矩阵，一般使用一个三维的浮点数数组 [height , width, 2] 来表示。其中，第一通道（height,width,0）表示（height,width）处像素点的x方向（水平方向或图像行向量方向）偏移矢量；而第二通道（height,width,1）表示（height,width）处像素点的y方向（竖直方向或图像列向量方向）偏移矢量。要注意的是：

光流数组中的数值大小表示偏移量，而数值正负表示偏移方向
光流数组的最终应用对象为二维图像帧的像素坐标(x,y)，而非(x,y)处的像素值
光流数组中的数值为浮点数，并非整数。这也就意味着光流warp操作后，t-1帧图像的像素坐标不一定会正好落到t帧图像的整数坐标上，可能还需要其他处理

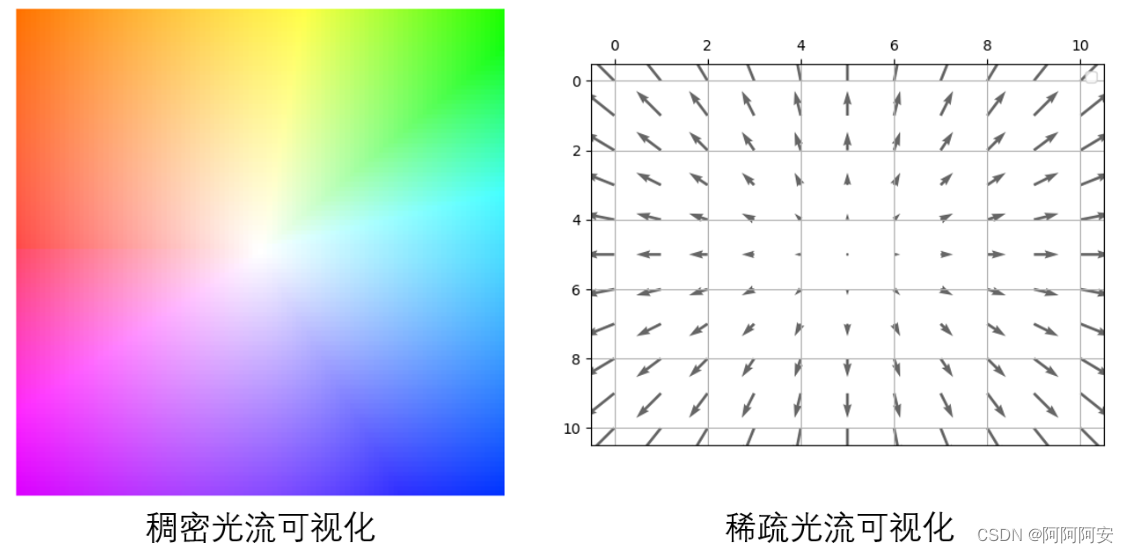
2.光流可视化

光流的计算结果是一个双通道的三维浮点数数组，很多时候我们需要将光流结果进行可视化来直观的反应物体的运动状态。作为一种矢量场，光流场在可视化的时候需要同时表现出各矢量的大小与方向，因此常见的光流可视化方法主要有以下两种：

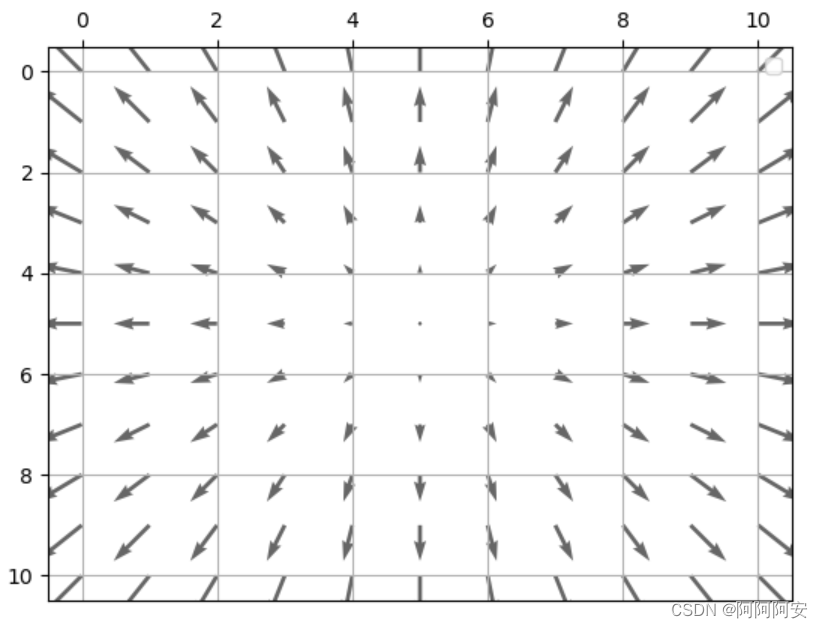
（1）光流箭头图

最简单的可视化方式就是用箭头表征光流，其中箭头的方向与长度分别代表各光流矢量的方向与大小，如下图所示。用箭头表征光流的优点在于简单直观，不过也存在一些不足。首先，通过这种方式对每个像素点的光流逐一采用箭头进行表征，当图像分辨率提升导致光流像素点非常稠密时，在有限区域内无法实现光流的完全表示；其次，随着箭头密度的增加，会使得图像非常凌乱。因此，光流箭头图一般适用于稀疏光流的可视化。
在这里插入图片描述

（2）光流色度图

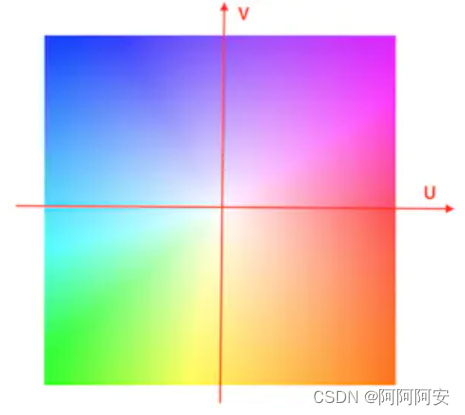
对于稠密光流来说，我们可以将光流计算的结果通过颜色模型对光流进行上色，以伪彩图（RGB彩图）的方式进行可视化。其中色调（或者说色相，即不同的颜色）表示运动方向，饱和度（或者说色调强度，即颜色的深浅）表示运动速度或偏移大小，而最中心位置代表没有运动和偏移发生，上色为白色。将光流计算结果转化为色度图的方法主要有两种我们将在下面介绍，整个色度图可视化参考的Color wheel如下所示：
在这里插入图片描述

（1）HSV颜色模型转化

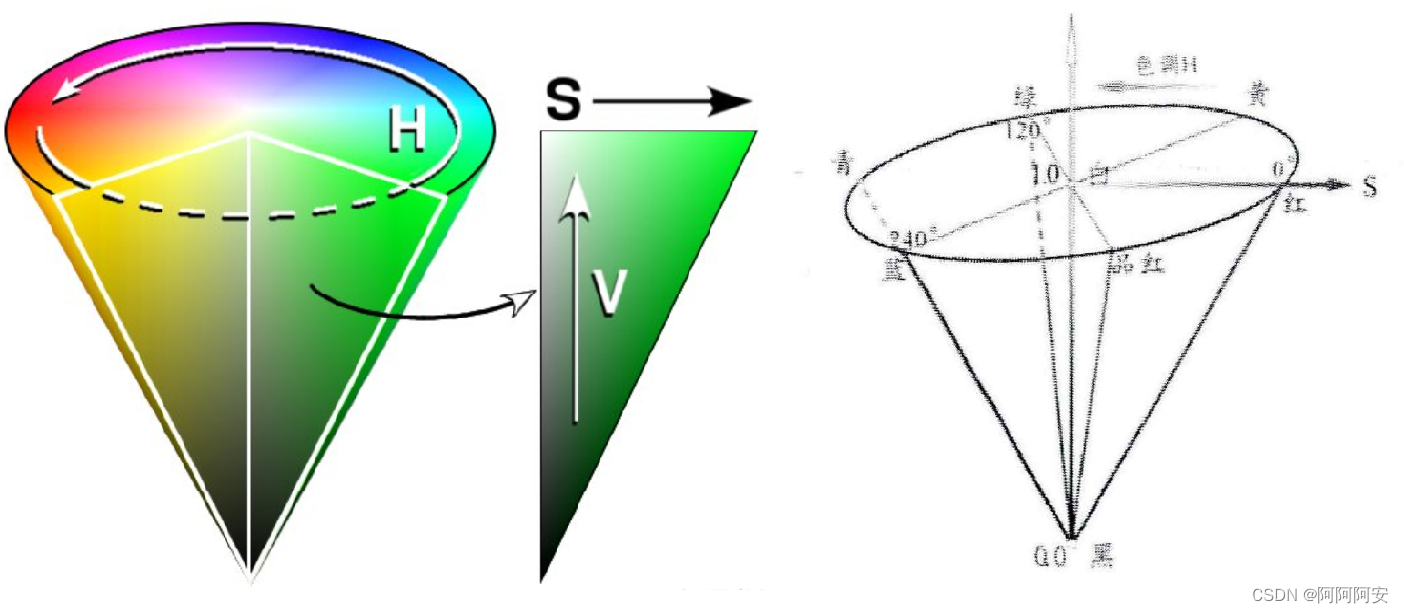
HSV是一种将RGB色彩空间表示为圆锥体的方法，其中Ｈ代表色相（色调、颜色种类），Ｓ代表饱和度（色调强度、颜色深浅），Ｖ代表明度（亮度）。HSV模型的三个主要组成部分介绍如下：

H（色调、色相）：该参数用一角度量来表示，取值范围为0°～360° 。若从红色开始按逆时针方向计算，红色为0°，绿色为120°，蓝色为240°。它们的补色是：黄色为60°，青色为180°，紫色为300°；
S（饱和度、色调强度）：径向比例，取值范围为0.0～1.0。饱和度表示颜色接近光谱色的程度，任一种颜色可以看成是某种光谱色与白色混合的结果。其中光谱色所占的比例愈大，颜色接近光谱色的程度就愈高，颜色的饱和度也就愈高，颜色也就越深。
V（明度、亮度）：竖直方向，取值范围为0.0(黑色，底部)～1.0(白色，顶部)，表示颜色明亮的程度。

使用该颜色模型进行光流可视化转化时，因为HSV模型图中第一个H维度，刚好用各种不同的颜色来表达角度，而光流的绝对值长度刚好又能被s和v维度表达（其实h和v只有一个自由度），因此可以很好的转化为HSV颜色模型下的表示。具体步骤为：

首先要将光流大小进行归一化处理，随后将光流方向映射至色相分量Ｈ。因为光流场为双通道三维数组，每个位置处的向量可以表示为直角坐标系下的坐标（x,y）。然后我们可以进一步将直角坐标系x和y转为极坐标系下的表示，其中极角 actan2(y,x) 就代表方向（映射为HSV模型的色调）
随后将光流大小映射至饱和度分量Ｓ，光流越大，饱和度也就会越大，而光流为０的地方则以白色显示。在极坐标系下，极径(x和y的平方和开根号) 就代表便偏移大小
最后，亮度分量V可以统一为一个值。比如为了让图像便于观察，可以固定调节至最亮255。最后再将HSV模型表示转化为RGB格式的伪彩图进行展示即可。

参考文章以及示例代码如下：

OpenCV官方：https://docs.opencv.org/3.4/d4/dee/tutorial_optical_flow.html

def viz_flow(flow):
    # 色调H：用角度度量，取值范围为0°～360°，从红色开始按逆时针方向计算，红色为0°，绿色为120°,蓝色为240°
    # 饱和度S：取值范围为0.0～1.0
    # 亮度V：取值范围为0.0(黑色)～1.0(白色)
    h, w = flow.shape[:2]
    hsv = np.zeros((h, w, 3), np.uint8)
    # cv2.cartToPolar(x, y[, magnitude[, angle[, angleInDegrees]]]) → magnitude, angle
    #	- params x,y:直角坐标系的横坐标、纵坐标，ndarray 多维数组，浮点型。默认为弧度制
    #	- return magnitude, angle：极坐标系下的极径值、极角值，ndarray 多维数组，与输入的 x, y 具有相同的尺寸和数据类型
    mag, ang = cv2.cartToPolar(flow[...,0], flow[...,1])
    hsv[...,0] = ang*180/np.pi/2 # 弧度转化为角度
    hsv[...,1] = cv2.normalize(mag,None,0,255,cv2.NORM_MINMAX) #标准化
    # flownet是将V赋值为255, 此函数遵循flownet，饱和度S代表像素位移的大小，亮度都为最大，便于观看
    # 也有的光流可视化讲s赋值为255，亮度代表像素位移的大小，整个图片会很暗，很少这样用
    hsv[...,2] = 255
    # cv2.cvtColor(frame,COLOR_STYLE) 改变图像的颜色空间，opencv中默认的颜色空间是BGR
    # backward conversions HSV to RGB/BGR with H range 0..180 if 8 bit image
    bgr = cv2.cvtColor(hsv,cv2.COLOR_HSV2BGR)
    return bgr

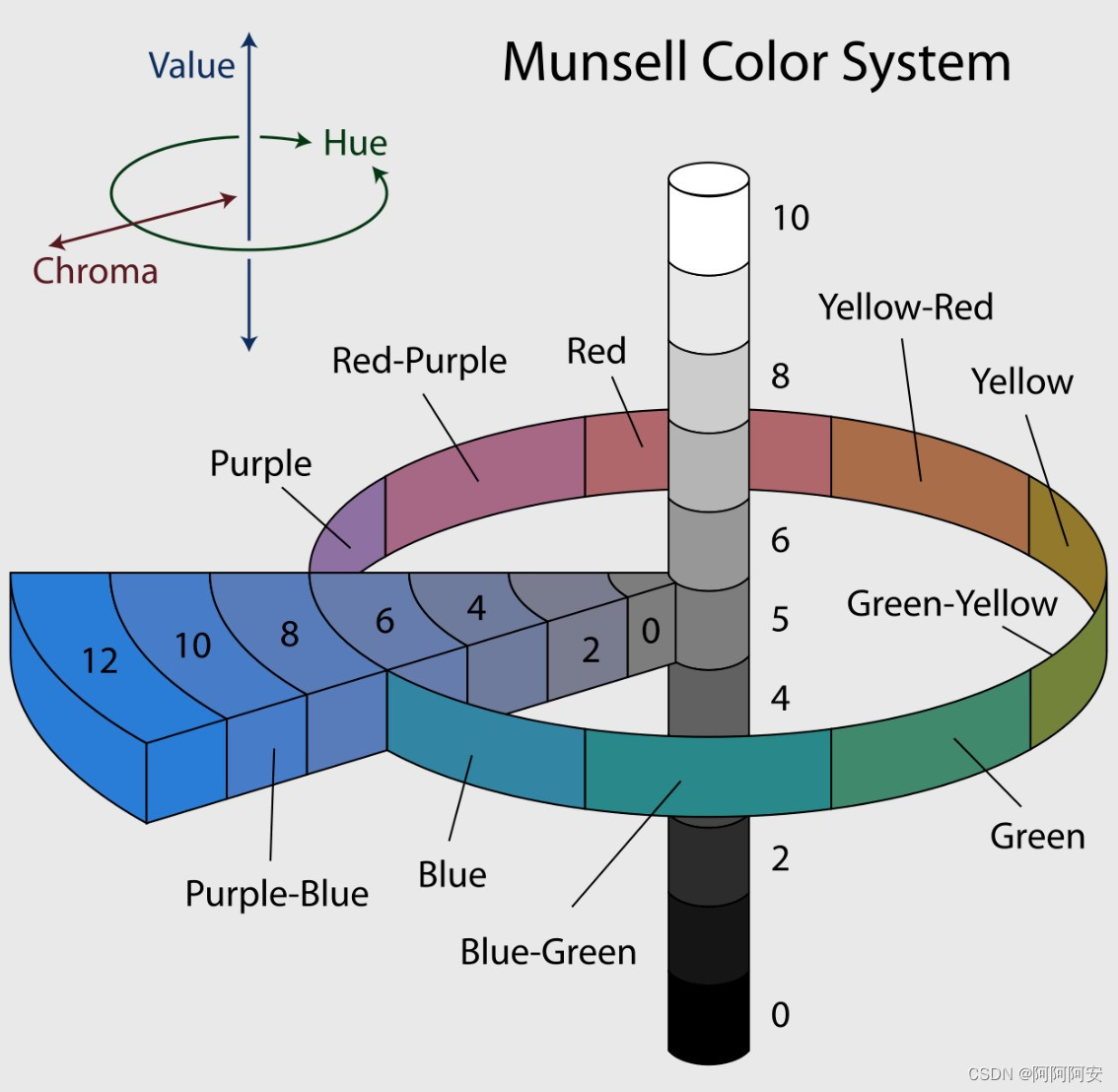
（2）孟塞尔颜色系统转化

该方法使用孟塞尔颜色系统（MunsellColor System，Wiki）来转化光流结果。MunsellColor System 是美国艺术家阿尔伯特孟塞尔（Albert H. Munsell，1858－1918）在1898年创制的颜色描述系统，它使用圆柱形将颜色空间大致划分，具体知识可以自行了解。该方法在很多文章中（FlowNet、PWC-Net等）都用来对光流计算结果进行可视化，得到了大量的验证。
在这里插入图片描述

参考文章以及示例代码如下：

可直接用的可视化工具：https://github.com/tomrunia/OpticalFlow_Visualization
参考论文：《A Database and Evaluation Methodology for Optical Flow》

import numpy as np

def make_colorwheel():
    """
    Generates a color wheel for optical flow visualization as presented in:
        Baker et al. "A Database and Evaluation Methodology for Optical Flow" (ICCV, 2007)
        URL: http://vision.middlebury.edu/flow/flowEval-iccv07.pdf
    Code follows the original C++ source code of Daniel Scharstein.
    Code follows the the Matlab source code of Deqing Sun.
    Returns:
        np.ndarray: Color wheel
    """

    RY = 15
    YG = 6
    GC = 4
    CB = 11
    BM = 13
    MR = 6

    ncols = RY + YG + GC + CB + BM + MR
    colorwheel = np.zeros((ncols, 3))
    col = 0

    # RY
    colorwheel[0:RY, 0] = 255
    colorwheel[0:RY, 1] = np.floor(255*np.arange(0,RY)/RY)
    col = col+RY
    # YG
    colorwheel[col:col+YG, 0] = 255 - np.floor(255*np.arange(0,YG)/YG)
    colorwheel[col:col+YG, 1] = 255
    col = col+YG
    # GC
    colorwheel[col:col+GC, 1] = 255
    colorwheel[col:col+GC, 2] = np.floor(255*np.arange(0,GC)/GC)
    col = col+GC
    # CB
    colorwheel[col:col+CB, 1] = 255 - np.floor(255*np.arange(CB)/CB)
    colorwheel[col:col+CB, 2] = 255
    col = col+CB
    # BM
    colorwheel[col:col+BM, 2] = 255
    colorwheel[col:col+BM, 0] = np.floor(255*np.arange(0,BM)/BM)
    col = col+BM
    # MR
    colorwheel[col:col+MR, 2] = 255 - np.floor(255*np.arange(MR)/MR)
    colorwheel[col:col+MR, 0] = 255
    return colorwheel


def flow_uv_to_colors(u, v, convert_to_bgr=False):
    """
    Applies the flow color wheel to (possibly clipped) flow components u and v.
    According to the C++ source code of Daniel Scharstein
    According to the Matlab source code of Deqing Sun
    Args:
        u (np.ndarray): Input horizontal flow of shape [H,W]
        v (np.ndarray): Input vertical flow of shape [H,W]
        convert_to_bgr (bool, optional): Convert output image to BGR. Defaults to False.
    Returns:
        np.ndarray: Flow visualization image of shape [H,W,3]
    """
    flow_image = np.zeros((u.shape[0], u.shape[1], 3), np.uint8)
    colorwheel = make_colorwheel()  # shape [55x3]
    ncols = colorwheel.shape[0]
    rad = np.sqrt(np.square(u) + np.square(v))
    a = np.arctan2(-v, -u)/np.pi
    fk = (a+1) / 2*(ncols-1)
    k0 = np.floor(fk).astype(np.int32)
    k1 = k0 + 1
    k1[k1 == ncols] = 0
    f = fk - k0
    for i in range(colorwheel.shape[1]):
        tmp = colorwheel[:,i]
        col0 = tmp[k0] / 255.0
        col1 = tmp[k1] / 255.0
        col = (1-f)*col0 + f*col1
        idx = (rad <= 1)
        col[idx]  = 1 - rad[idx] * (1-col[idx])
        col[~idx] = col[~idx] * 0.75   # out of range
        # Note the 2-i => BGR instead of RGB
        ch_idx = 2-i if convert_to_bgr else i
        flow_image[:,:,ch_idx] = np.floor(255 * col)
    return flow_image


def flow_to_color(flow_uv, clip_flow=None, convert_to_bgr=False):
    """
    Expects a two dimensional flow image of shape.
    Args:
        flow_uv (np.ndarray): Flow UV image of shape [H,W,2]
        clip_flow (float, optional): Clip maximum of flow values. Defaults to None.
        convert_to_bgr (bool, optional): Convert output image to BGR. Defaults to False.
    Returns:
        np.ndarray: Flow visualization image of shape [H,W,3]
    """
    assert flow_uv.ndim == 3, 'input flow must have three dimensions'
    assert flow_uv.shape[2] == 2, 'input flow must have shape [H,W,2]'
    if clip_flow is not None:
        flow_uv = np.clip(flow_uv, 0, clip_flow)
    u = flow_uv[:,:,0]
    v = flow_uv[:,:,1]
    rad = np.sqrt(np.square(u) + np.square(v))
    rad_max = np.max(rad)
    epsilon = 1e-5
    u = u / (rad_max + epsilon)
    v = v / (rad_max + epsilon)
    return flow_uv_to_colors(u, v, convert_to_bgr)

三.光流 warp

warp 可以翻译为扭曲、变形、映射的意思，光流 warp 操作的含义就是将计算的结果光流作用到目标图像帧上去，以获得在该光流影响偏移或运动变换后的结果图像帧。比如有 t->t+1图像帧的光流，我们将其作用到图像帧t上，则在理想状态下的作用结果就应该是图像帧t+1，整个变换过程就是一种光流的warp操作。光流warp主要包括 forward warp 和 backward warp两种方式，接下来将分别介绍。
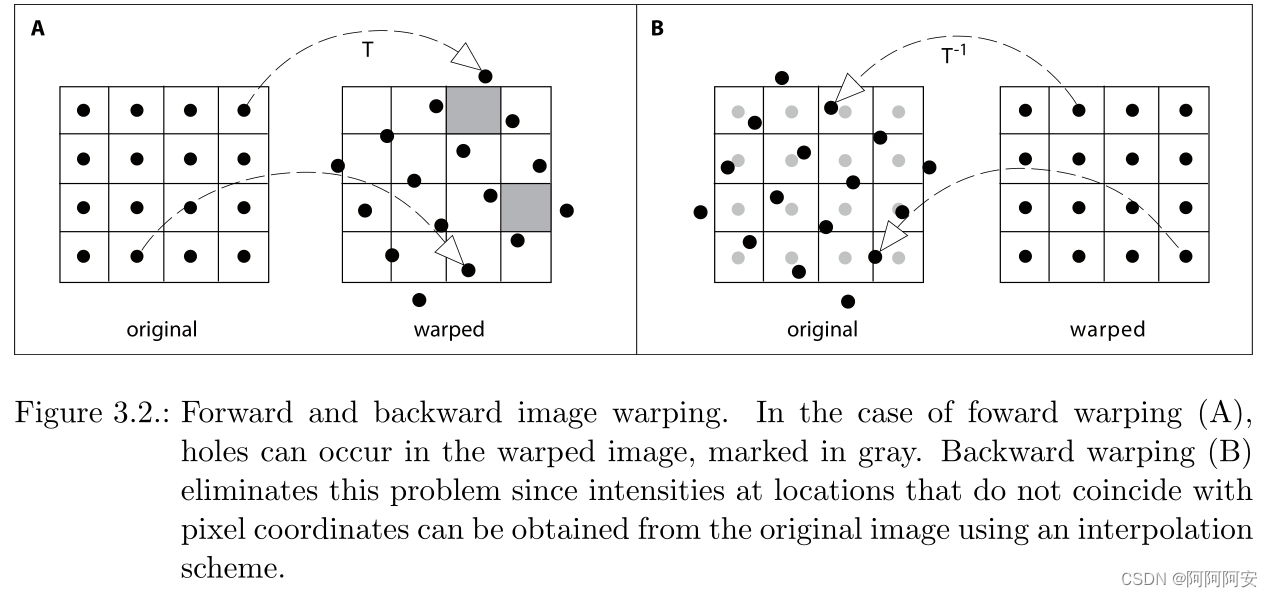
在这里插入图片描述

1.fordward warp

若存在前后两帧相邻图像（或左图右图） $I_1,I_2$ ，对应 $I_1 \rightarrow I_2$ 的光流 Flow 为 $F_{1\rightarrow2}$ （光流就是两张图像上对应点的偏移关系），则在 forward warp 操作下，第一帧图像的像素点值 $I_1(x,y)$ 会出现在第二帧图像上的 $I_2((x,y)+F_{1\rightarrow2})$ 坐标位置上，即 $I_1(x,y) = I_2(x+\Delta x,y+\Delta y)$ ，其中 $F_{1\rightarrow2}(x,y) = (\Delta x,\Delta y)$ 。

forward warp 可以简单理解为“前向变形/扭曲”，即图像变换方向与光流的流向相同，这与我们的固有认知思维是一致的。比如使用 $I_1\rightarrow I_2$ 的光流，将 $I_1$ 变换到 $I_2$ 的视角，这就是一种 forward warp；
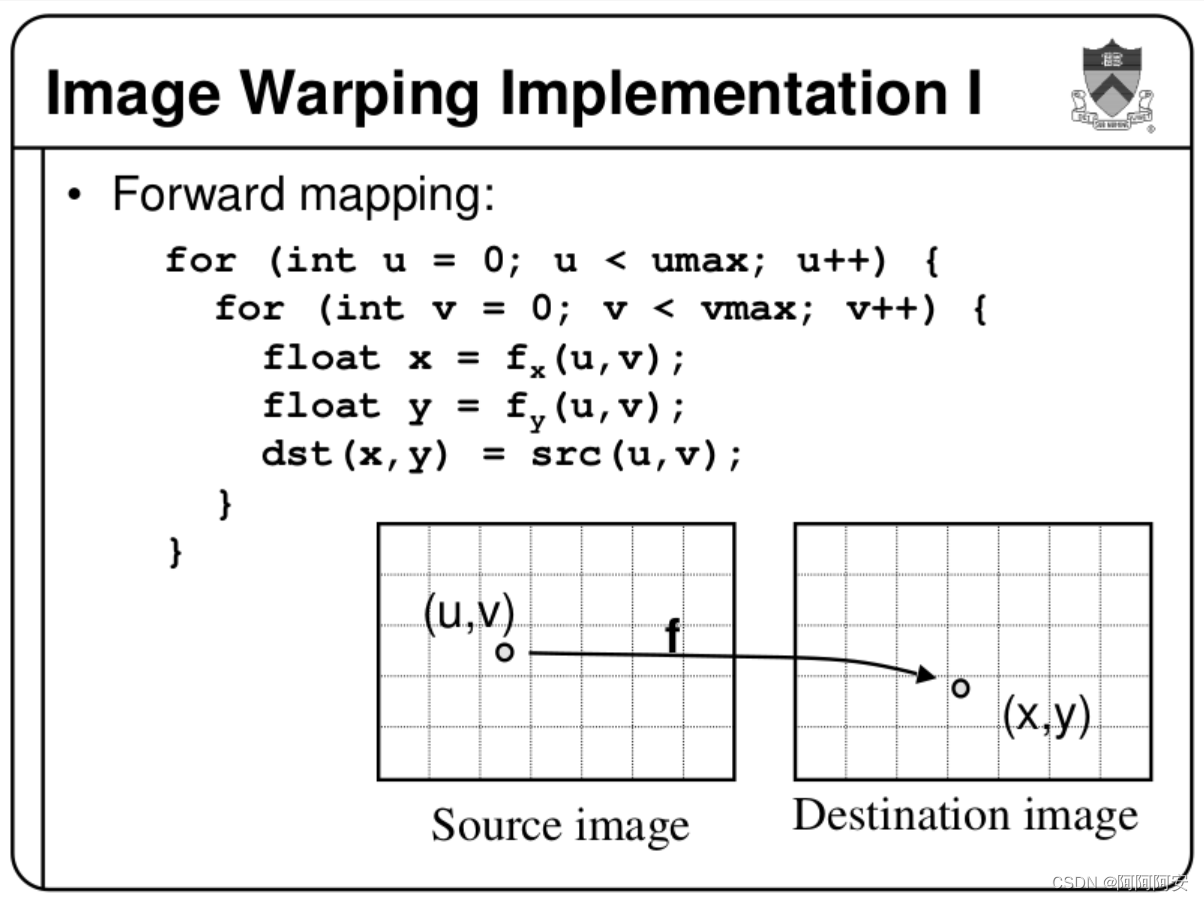
在这里插入图片描述

forward warp的实现思路为遍历source image中的每个点p_source，通过光流 $F_{Source\rightarrow Destination}$ 中点p_source处的坐标偏移量，计算后将其像素值投影到destination image中得到p_destination，如果p_destination的坐标不是整数，则一般会采用四舍五入取整或选择最近邻的方式。其简单实现代码如下：

im1 = torch.zeros_like(im0)
B = im0.shape[0]
H = im0.shape[2]
W = im0.shape[3]
round_flow = torch.round(flow)
for b in range(B):
    # 遍历source image中的每个点p_source
	for h in range(H):
		for w in range(W):
            # 获取投影到destination image中的对应坐标点p_destination，采用四舍五入取整
			x = w + int(round_flow[b, h, w, 0])
			y = h + int(round_flow[b, h, w, 1])
            # 判断映射位置是否在有效范围内，若在则赋值，否则保留zero
			if x >= 0 and x < W and y >= 0 and y < H:
				im1[b, :, y, x] = im0[b, :, h, w]
return im1

forward warp 的实现和思路非常简单，但是这也带来了很多问题：

空洞问题：forward warp 的这种映射关系既不是单射也不是满射，而是一种离散化的随机映射。这就会导致destination image中有的位置没有从source image中投影过来的点，或者有的位置同时有多个从source image中投影过来的点，所以会产生很多空洞，出现类似波纹的效果。其解决方案考虑如下：
- 多点映射：对于多个点同时映射到一个点的情况，我们可以选择“移动幅度”最大的那一个点，因为“移动幅度”更大的通常是前景，前景移动多，以保留前景为主。
- 无点映射： 这种情况一般考虑通过插值处理。但是destination image作为被投影帧，其每个位置的点不是均匀分布的，直接使用 bilinear 这种需要固定线性位置的插值算法比较困难，最简单的还是直接使用最近邻或取整。
当然也有一些人在专门研究如何解决 forward warp 的空洞问题，提出了很多新的思路和方法，比如 softmax-splatting 这篇文章。
技术限制： 因为在forward warp中多使用最近邻或取整的方式来取点，这就导致没法在 forward warp 中使用反向传播算法，使得其在深度学习中的应用不明显。
线程安全： 如果是在多线程、并行场景下，CUDA版本还有线程安全的问题，影响速度

2.backward warp

若存在前后两帧相邻图像（或左图右图） $I_1,I_2$ ，对应 $I_2 \rightarrow I_1$ 的光流 Flow 为 $F_{2\rightarrow1}$ ，则在 backward warp 操作下，第二帧图像的像素点 $I_2(x,y)$ 会在第一帧图像上的 $I_1((x,y)+F_{2\rightarrow1})$ 坐标位置范围内找值（相当于 $I_1$ 是已知的， $I_2$ 是未知的），即 $I_2(x,y) = I_1(x+\Delta x,y+\Delta y)$ ，其中 $F_{2\rightarrow1}(x,y) = (\Delta x,\Delta y)$ 。注意，backward warp 也存在找值时映射坐标不为整数的情况，但是由于 $I_1$ 是已知的， $I_2$ 是未知的，我们是对于 $I_2$ 的每个坐标 $(x, y)$ 在 $I_1$ 中 $(x+\Delta x,y+\Delta y)$ 处找值，所以不为整数的坐标可以在 $I_1$ 范围内通过双线性插值来近似计算，因此不会产生forward warp的空洞问题。

backward warp 可以理解为“后向变形/扭曲”，即图像变换方向与光流的流向相反，这与我们的固有认知思维恰好是不一样的。比如使用 $I_2\rightarrow I_1$ 的光流，将 $I_1$ 变换到 $I_2$ 的视角；或者使用 $I_1\rightarrow I_2$ 的光流，将 $I_2$ 变换到 $I_1$ 的视角，这就是一种 backward warp；
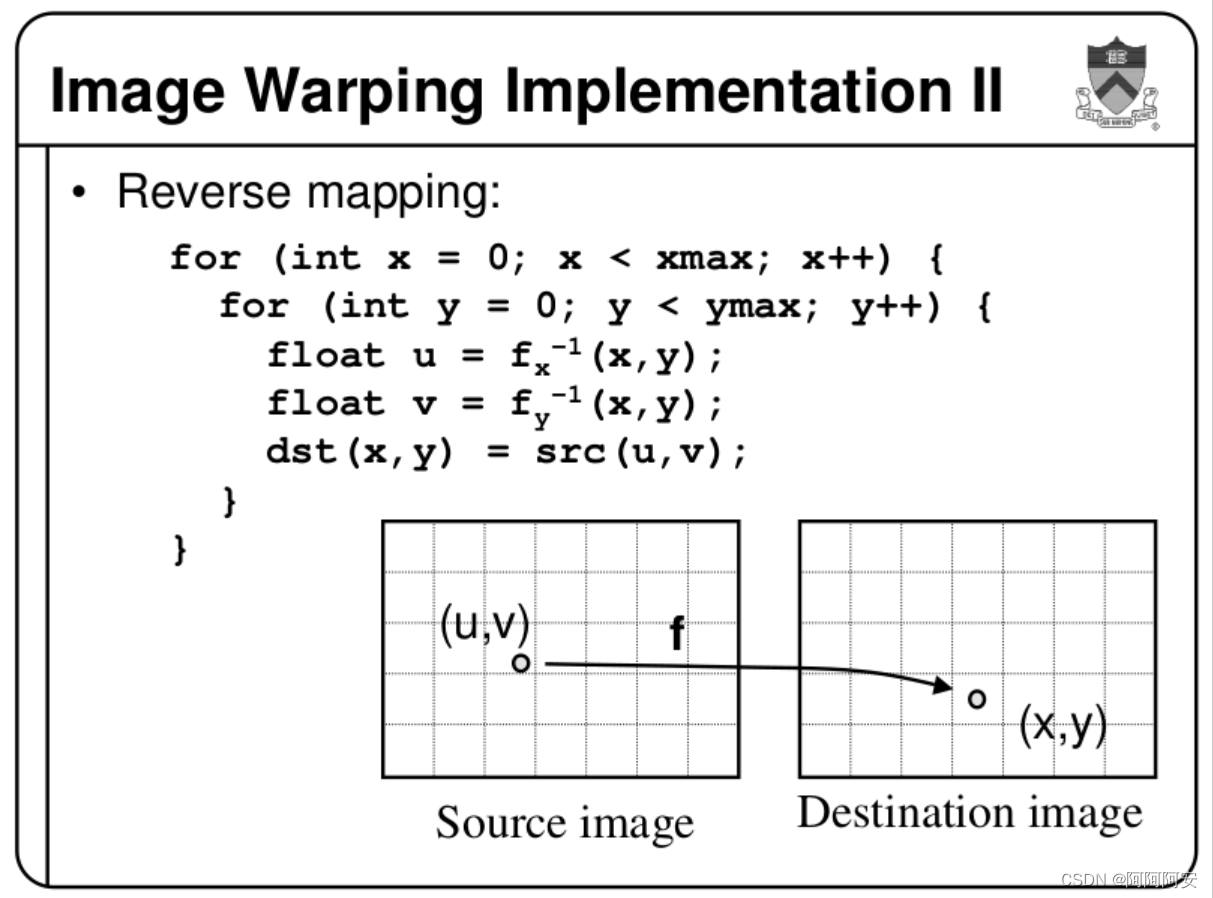
在这里插入图片描述

backward warp的实现思路为遍历destination image中的每个点p_destination，通过光流 $F_{Destination\rightarrow Source}$ 计算点p_destination在Source image中的对应点p_source，令p_destination的像素值等于p_source的值。如果p_source的坐标不是整数，则一般采用双线性插值的方式来近似计算（Source Image是已知的、参照的），因此不会产生的Forward Warping的问题。其简单实现代码如下：

def backward_warp(self, x, flo):
        """
        warp an image/tensor (im2) back to im1, according to the optical flow(im1->im2)
        x: [B, C, H, W] (im2)
        flo: [B, 2, H, W] flow
        """
        B, C, H, W = x.size()
        # mesh grid 
        xx = torch.arange(0, W).view(1,-1).repeat(H,1)
        yy = torch.arange(0, H).view(-1,1).repeat(1,W)
        xx = xx.view(1,1,H,W).repeat(B,1,1,1)
        yy = yy.view(1,1,H,W).repeat(B,1,1,1)
        grid = torch.cat((xx,yy),1).float()

        if x.is_cuda:
            grid = grid.cuda()
        vgrid = Variable(grid) + flo

        # scale grid to [-1,1] 
        vgrid[:,0,:,:] = 2.0*vgrid[:,0,:,:].clone() / max(W-1,1)-1.0
        vgrid[:,1,:,:] = 2.0*vgrid[:,1,:,:].clone() / max(H-1,1)-1.0

        vgrid = vgrid.permute(0,2,3,1)  
        # 双线性插值 functional.grid_sample
        output = nn.functional.grid_sample(x, vgrid)
        # implementational hack in PyTorch0.2 for the warping function.
        mask = torch.autograd.Variable(torch.ones(x.size())).cuda()
        mask = nn.functional.grid_sample(mask, vgrid)

        # if W==128:
            # np.save('mask.npy', mask.cpu().data.numpy())
            # np.save('warp.npy', output.cpu().data.numpy())
        
        mask[mask<0.9999] = 0
        mask[mask>0] = 1
        
        return output*mask

backward warp 的实现和思路也非常清晰，主要是如何合理地使用插值来处理数据。backward warp也存在一些优缺点分析如下：

算法优化：backward warp 引入各种插值来计算坐标，不会使得图像被分裂或产生空洞问题，并且backward warp是可以进行反向传播计算的，这使得backward warp的应用更加广泛和简单，尤其在深度学习领域中。
重影问题： backward warp会在图像中产生重影问题，这是由于这种非保序变换会使得像素间的位置关系在映射前后可能发生改变，当前景和背景产生相对运动时就会出现重影、留白等现象，这种歧义与无效信息产生的本质原因是相对运动形成的遮挡。对重影问题的通用解决方法是引入一个遮挡掩码 mask 来细化图像。