这场数学和思维偏多，特别是数学，五个小时过于充实了，而且更加考验你的心态。
这场不乏码量大的毒瘤题，也不乏人类智慧妙妙题。

A 不断减损的时间
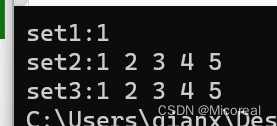
题意 给定一个数组$a$，我们可以执行任意次操作，该操作定义为选择一个偶数并除以2，问数组和最小为多少， $-1e9<=a_i<=1e9,n<=2e5$ 。
思路 贪心，负数考虑不对他进行改变，因为改变就会变大，正数是能除以2就除以2 。
代码

B 勉强拼凑的记忆
题意 小红想用恰好$n$块木块凑成正方形，木块是为长不超过$(n+1)/2$，宽为1的木块，问你能够拼出的正方形最大时多大， $n<=1e9$ 。
思路 考虑我们先凑出长为$(n+1)/2$的正方形，用去了$(n+1)/2$的木块，然后我们考虑向右向下延伸，我们可以发现可以表示成下图

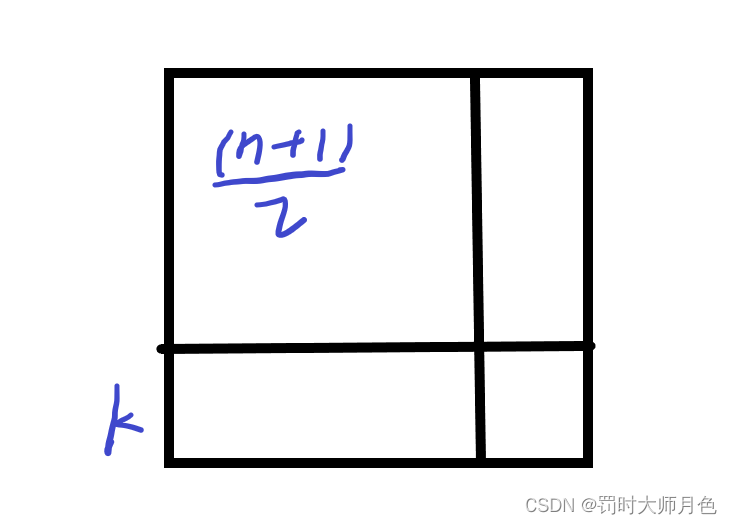
如果我们想要$k$每次增加1，就要花费三个木块，所以答案为$(n+1)/2+n/2/3$
代码

C 忽远忽近的距离
题意 这是一道构造题 ，要求构造一个数组$a$，对于所有的$a_i$满足$2<=|a_i-i|<=3$ , $n<=2e5$。
思路 考虑模数构造，用了一个比较麻烦的思路，我们观察样例，发现长度为4、5、6时有合法解，我们可以考虑对模数分类讨论，当$n$%4 为 0 时，我们可以按长度为4的方式对于所有的相邻4个块类比构造，当$n$%4 为 1时，我们可以向前抽一个长度为4的区间，然后我们要构造长度为5的区间，当$n$%4 为 2时，我们类似地向前借一个区间构造长度为6的区间，当$n$%4 为 3时，这个时候不能用长度为7的区间，长度为7是无解情况，我们用长度为11的区间构造，剩下的就是每四个区间按上述方式构造，然后不同长度的区间的合法情况可以通过写暴力获得，剩下的就是代码实现问题。
代码

D 宿命之间的对决
题意 小红和小紫正在玩游戏， 给你一个数字$n$, 小红小紫轮流操作，每轮可以选择$n$的因子，并且让$n$减去这个因子，谁先在当前轮把$n$减到0就输 , $n<=1e18$。
sample

input
2
output
kou

解释：小红先手取，只能取1（若取2，则小红直接失败），将$n$变成1。此时小紫只能取1，所以小红获胜。

思路 当时看完题也是脑子晕乎乎的，然后想到有没有可能双方一个一个取的情况，于是尝试对$n$判断奇偶性，即判断$n$模2的模数，如果当前自己先手，模数为0，这是先手必胜态，因为模数为零一定是大于等于2的偶数(若要是为0游戏结束) ，所以一定能先手必胜。模数为1是否是先手必败态呢？答案是是的，若我们为先手必败态，我们考虑想办法让对面对先手必败，即当前能够拿出偶数因子(奇数减去偶数还是偶数), 考虑是否有这个情况，如果因子为偶数，一定不可能有对应的数与其相乘等于奇数，所以该情况不成立，因此先手必败态每次操作后转移给对方的一定是先手必胜态。因此该题得证，判断$n$的奇偶性即可。
代码

E 公平守望的灯塔
题意 给你两个点$A,B$问找一顶点$C$,并且能够能以$AB$为斜边构成等腰直角三角形,给定$A,B$的坐标为整数，所求的$C$的坐标也要求为整数，若不合法输出$NoAnswer!$ 。坐标系的范围为$[-1e9,1e9]$ 。
思路 求$AB$的中点E，将$AE$旋转90度即可，手动调试可以发现无解情况为，$dx为abs(X_a,X_b),dy为abs(Y_a,Y_b)$ , $dx$和$dy$的奇偶性不同。
代码

F 迎接终结的寂灭
题意 输出42
代码

G 严肃古板的秩序
题意 给你一个运算表达式，保证是一个合法的运算式子。即

运算符号可填’+’ , ‘-’ , ‘#’,其中’#‘的运算a # b表示为$a^a模b$ 。
思路 发现’?‘的个数只有十二个，考虑跑3 ¹²的暴力即可，需要注意的是可能会报long long,在’#'运算时可以采用$int128$ , 提前取模或者龟速乘的方式避免爆long long。
代码

H 穿越万年的轮回
题意

思路
我们可以发现子串为$"red"$的情况很好统计，两种字符串$red和edr$，$red$只会出现在red和两个edr之间，无其他情况。
接下来对三种操作分类讨论。
第一种操作，加上字符串$red$后，答案加1
第二种操作，加上字符串$edr$后，我们需要考虑前一个位置是哪种字符串，如果前一个位置是$edr$字符串，则答案加1，否则没有贡献。
第三种操作，我们需要考虑空串的情况，空串则没有贡献，然后考虑重复10次，对答案的影响是乘10的影响，然后我们发现有一种特例是头部尾部都是”edr"字符串时，会对答案多贡献9个$red$。
然后期望考虑维护概率，然后$1-n$的顺序去做，一定要一直维护$pi\ast 操作次数$的形式即可。如果有概率论基础的人可以在一定时间内写出来。
代码+思维整体难度偏难 。
代码

I 灵魂碎片的收集
题意

思路
本场最有意思的一道妙妙题，这题考察了一个非常偏门但是有意思的一个结论，当时看到这题我就从质因子分解入手，发现不是很可做，然后自己打了一个表，观察一下奇数的合法解有哪些，观察过程中发现一些数很有意思，比如说 11 对应 21 ， 21 对应 51 ，然后拆一下质因子发现他们的和为$n-1$且有两个，然后猜想是不是所有的偶数都能分解为质数，然后搜了一下哥德巴赫猜想，然后奇数情况就做完了。
现在开始讨论偶数情况，题目保证$x-1$和$x-3$至少有一个为质数，一直在思考这两个条件的作用，$x-3$的情况非常容易想到可以变成$1+2+(x-3)$的形式，对应的数就是$2\ast (x-3)$，然后在思考$(x-1)$的情况，一直没有想到解法，然后我从打表的数据中找一些满足只有$(x-1)$为质数的情况$(38-1369)$ ，然后$1369$的质因子分解为$37\ast 37$，然后就得出来若$(x-1)$为质数时，答案为$(x-1{)}^2$。这道题就做完了，需要特判$1，3，7$情况即可。
代码

K 永恒守候的爱恋
题意

思路
我们有一个结论可以快速求因子数量，我们对其质因子分解，p1^a1*p2^a2*p3^a3形式的因子个数为$(a1+1)\ast (a2+1)\ast (a3+1)$然后我们就可以发现每加一个质因子对答案的影响是，当前质因子的个数为$m$，对答案的影响为乘上$(m+1)/m$，然后我们发现出现1次对应加上的倍数是$2,3/2,4/3$,慢慢变小的，按照贪心的思路，我们应该让倍数增加最大的放在前面，即一层一层的把所有的质数全部加上去，简要的说就是每一步我们扫一遍每个数拿出去一个去加到数组上。
举例如下
我们有4个2，3个3，5个7，4个11。
我们每一层加到数组的顺序为 $[2,3,5,7],[2,3,5,7],[2,3,5,7],[2,5,7],[5]$这样子一定是最优的，然后暴力模拟该过程即可，我们可以考虑按块去模拟这个过程，因为我们发现层数最多$2e5$层，考虑暴力$2e5$去做操作， 我们用差分维护每层有多少个数，然后每层一个一个加上数的过程本质上可以看成一个等比数列，维护长度和首项以及数列的上一项的值便可以算出答案。
代码