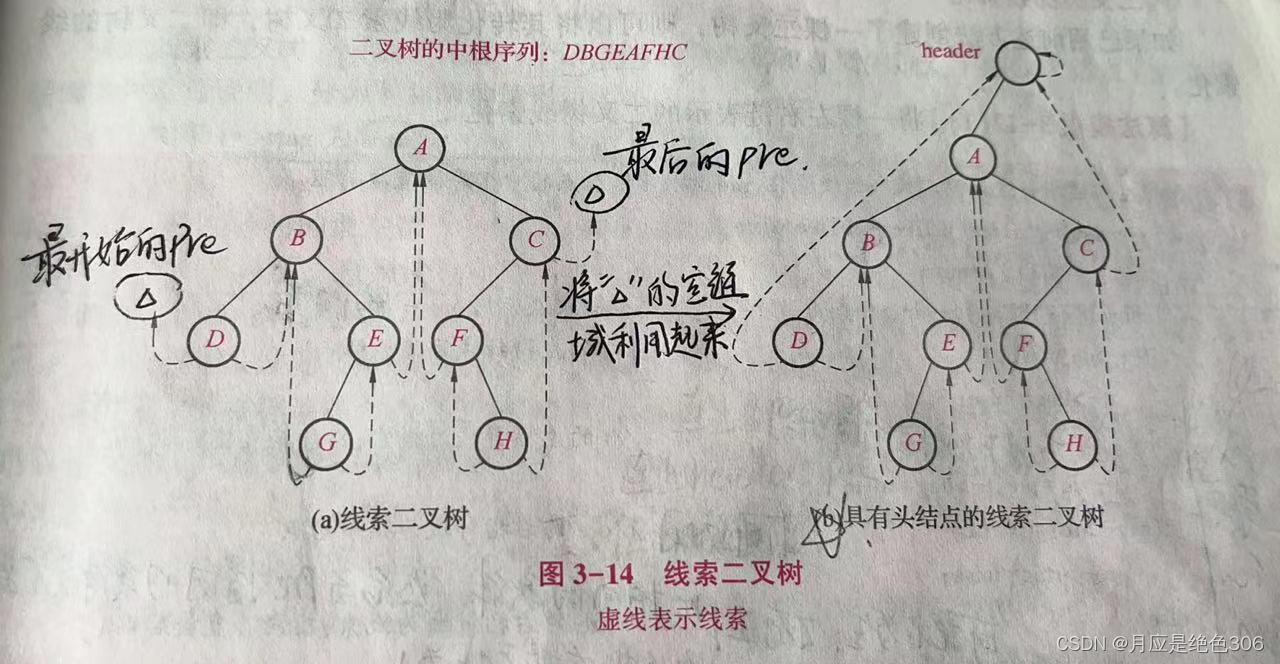
二维矩阵的元素和
- 1.背景
- 2.原理
- 3.实现
1.背景
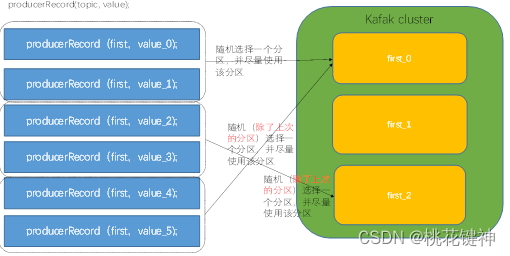
对矩阵元素进行求和,或者求子矩阵的元素和;给定矩阵左上角坐标(x1,y1)和右下角坐标(x2,y2); 如何快速求出 以(x1,y1),(x2,y2)围成的矩阵的元素和?
例如:有4x4矩阵A, 求A中所有元素和; 即求以左上角[0,0], 右下角[3,3]的矩阵的元素和
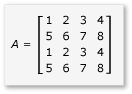
一种方法是暴力枚举,从左至右,从上至下依次加上每个元素:
int matrixElementSum(vector<vector<int>> &matrix, int x1,int y1, int x2, int y2) {
int sum = 0;
for (int i = x1; i <= x2; i++ ) { /
for (int j = y1; j <= y2; j++ ) {
sum += matrix[i][j];
}
}
return sum
}
但是,如果需要求多个子矩阵的和,需要枚举多次,有没有一种方法,以O(1)的时间复杂度求出矩阵的元素和?可以通过预处理求出每个矩阵的元素和,然后让两个矩阵相减求得任意子矩阵的元素和。
2.原理
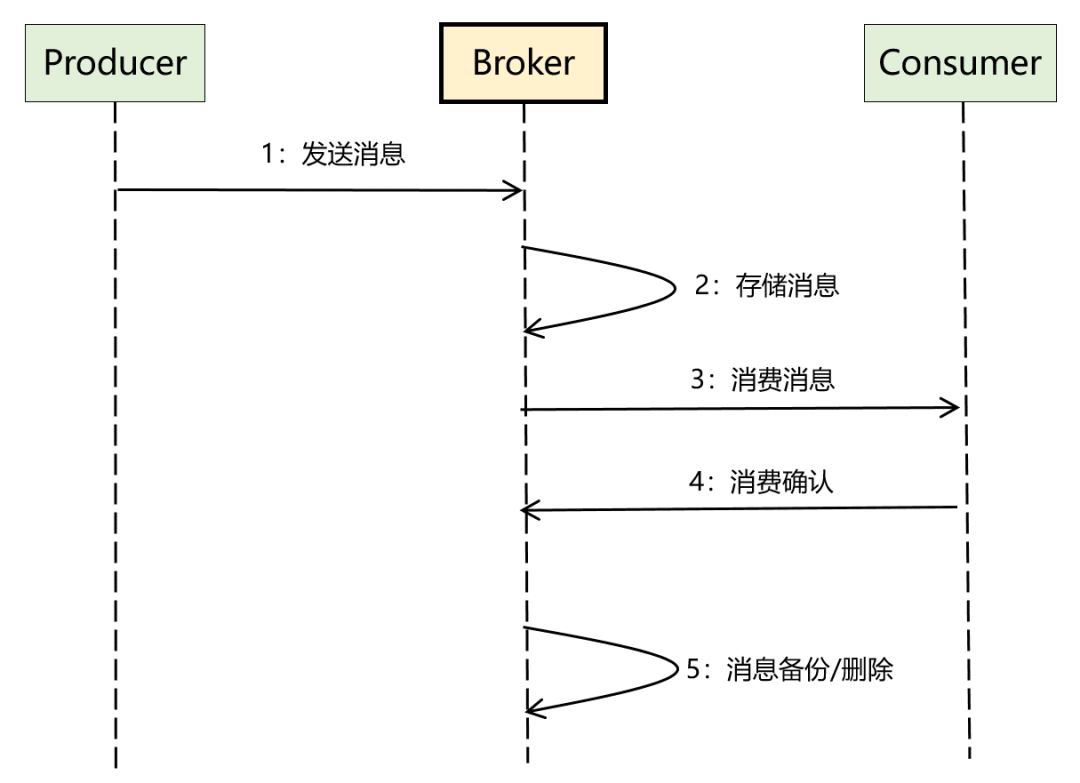
如何求得M的元素和?求前缀和再作差
首先,将矩阵M分成4块,
A:红色矩形
B:蓝色矩形
C:绿色矩形
D:紫色矩形
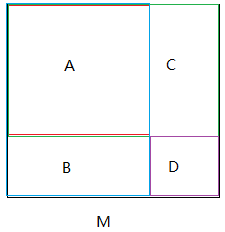
矩阵A、B、C、D的元素和记为 Sa,Sb,Sc,Sd; 那么矩阵M中所有元素的和S可以表示为:
S = Sc+Sb-Sa+Sd;
因为B, C中均包含了A, Sa加了两次,所以是Sb+Sc-Sa, 最后加上D部分的元素和Sd, 即为S的元素和;
S的递推式可以写成
S = Sc+Sb-Sa+Sd; C的右下角坐标(i-1,j), B的右下角坐标(i,j-1), A的右下角坐标(i-1,j-1), D的坐标(i,j), S的递推式
S[i][j] = S[i][j-1] + S[i-1][j] - S[i-1][j-1] + M[i][j];
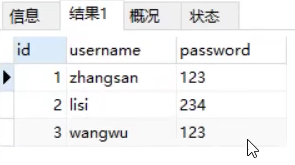
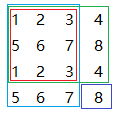
举个例子:
矩阵M如下图,矩阵M的元素和S, 矩阵下标从0开始, 根据上述递推公式
S[3][3] = S[3][2] + S[2][3] - S[2][2] + M[3][3]
以0,0为左上角,i,j (0 <= i <= m, 0 <= j <= n) 为右下角的矩阵元素和矩阵为
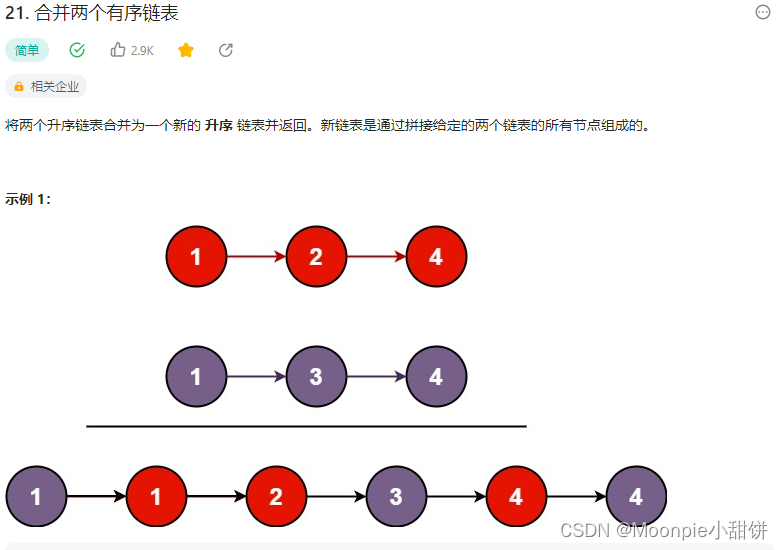
如果要求其中任意矩阵的元素和,例如右上角(1,1),坐下角(3,3)子矩阵的元素和, 即下图中子矩阵的元素和
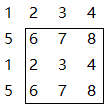
可以用整个矩阵的元素和S,减去蓝色部分子矩阵元素和,减去绿色部分子矩阵元素和,加上红色部分子矩阵元素和(因为减了两次), 于是,上一张图中的矩阵元素和为
S1 = S[3][3] - S[3]0] - S[0][3] + S[0][0]
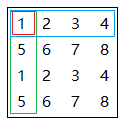
记右上角(row1,col1),坐下角(row2,col2), 子矩阵元素和计算公式
S1 = S[row2][col2] - S[row2][col2] - S[row1][col2] + S[row1][col1]
3.实现
#include<iostream>
#include<vector>
#include<string.h>
#define N 101
using namespace std;
int A[N][N];
int S[N][N];
int main() {
int n = 6;
memset(A,0,sizeof(A));
memset(S,0,sizeof(S));
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
A[i][j] = j+1;
cout << A[i][j] << " ";
}
cout << endl;
}
cout << "---sum---" << endl;
//S[i][j] = S[i-1][j]+S[i][j-1]-S[i-1][j-1]+F[i][j]
//S[0][j] = S[0][j-1]+A[0][j]
//S[i][0] = S[i-1][0]+A[i][0]
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (i==0 && j==0) {
S[i][j] = A[i][j];
} else if (i==0) {
S[i][j] = S[i][j-1] + A[i][j]; //A[0][j], 第一行
} else if(j==0) {
S[i][j] = S[i-1][j] + A[i][j]; //A[i][0], 第一列
} else {
S[i][j] = S[i-1][j] + S[i][j-1] - S[i-1][j-1] + A[i][j];
}
cout << S[i][j] << " ";
}
cout << endl;
}
cout << "---sub matrix sum---" << endl;
//S1 = S[x2][y2] - S[x2][y1] - S[x1][y2] + S[x1][y1]
int x1,x2,y1,y2;
// 1 1 4 4
cin >> x1 >> y1 >> x2 >> y2;
int S1 = S[x2-1][y2-1] - S[x2-1][y1-1] - S[x1-1][y2-1] + S[x1-1][y1-1];
cout << S1 << endl;
return 0;
}
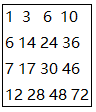
输出:
1 2 3 4
5 6 7 8
1 2 3 4
5 6 7 8
—sum—
1 3 6 10
6 14 24 36
7 17 30 46
12 28 48 72
—sub matrix sum—
1 1 4 4
51
参考:
https://www.bilibili.com/video/BV1oz4y1S7px?spm_id_from=333.880.my_history.page.click