1.引言：

二叉树的三种遍历方法能将二叉树中的结点按某种方式生成一个线性序列，能将一个非线性结构进行线性化操作。但随之也产生两个问题：

• 遍历效率低
  在采用左右链表示方法作为二叉树的存储结构时，当二叉树更新后，并不能直接得到某个结点的直接前驱和直接后继，只能对二叉树进行重新遍历，
• 浪费存储空间
  在一个具有n个结点的二叉树中，空指针域的数量为n+1，占用存储空间

 于是，我们希望空间最大化利用的同时，能够记录前驱后继结点。为此我们提出线索二叉树的概念。

2.线索二叉树

线索二叉树是指在二叉树上添加线索。通过线索二叉树，可以求任何一个结点的直接前驱和直接后继。 

现将某结点的空链域赋予特定含义，指向该结点的前驱后继，定义规则如下：

• 若结点的左子树为空，则该结点的左孩子指针指向其前驱结点
• 若结点的右子树为空，则该结点的右孩子指针指向其后继结点

这种指向直接前驱和直接后继的指针（链域）称为线索，将一棵普通的二叉树以某种次序遍历，并添加线索的过程称为线索化。

下面以中根线索二叉树为例进行说明

中根线索二叉树是指在左右链所表示的二叉树中，将结点的空左链域指向二叉树中中根序列中该结点的直接前驱，将结点的空右链域指向二叉树中根序列中该结点的直接后继。 

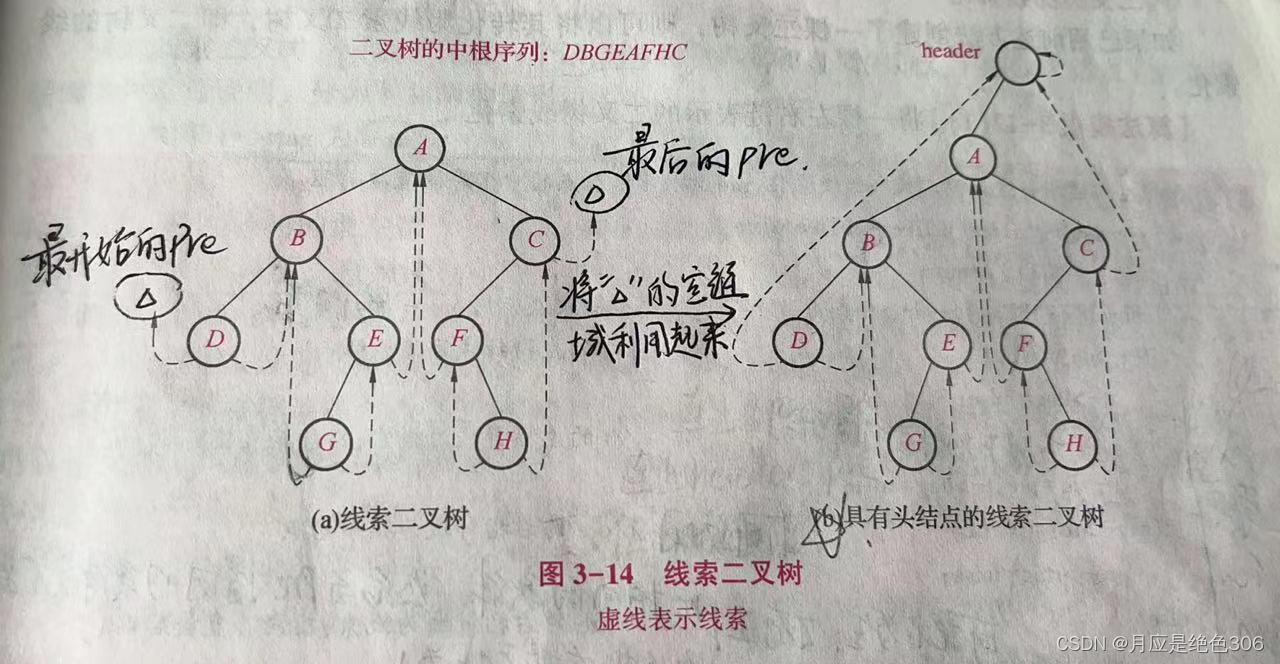
注意：（a）图最后的 pre 和 t 都指向 C ；（b）中一开始header是D的线索前继，自身的线索后继，最后是C的右节点。

任意一个二叉树的左右链表示法都可以转化为线索二叉树，一个结点的左(右)链域可能是指向该结点的左(右)孩子，也可能指向该结点的直接前驱(后继）。为了区分结点的孩子链域是否为线索，于是为左右链域各添加一个标识：

(1) ltag：判别左链域lc是否为线索。当ltag=true 时，lc为指向当前结点直接前驱的线索，否则lc指向当前结点的左孩子结点；

(2) rtag：判别右链域rc是否为线索。当rtag=true 时，rc为指向当前结点后继的线索，否则rc指向当前结点的右孩子结点。

 转化过程分为如下两步：

        第一步为线索二叉树添加一个头结点header，根据前面的规定对头结点进行设置，然后从二叉树的根结点出发为二叉树添加线索，这一步在函数thTree_create 中实现。

        第二步为二叉树添加线案，方法是利用中根遍历方法遍历每一个结点，在遍历过程中需要记录当前结点t的上一个结点 pre，在第一步中设置pre 的初始值为header。如果t 的左孩子为线索，则t的直接前驱为pre；如果pre 的右孩子为线索，则pre 的直接后继为t。

        当第二步完成后，pre 应该为中根序列的最后一个结点，需要按要求设置其后继。

3.完整代码展示 

#include<iostream>
using namespace std;
typedef char datatype;

//左右链指针表示的线索二叉树的结点的定义
typedef struct thNode {
    datatype data;
    thNode* lc, * rc;
    bool ltag, rtag;
    thNode() :lc(NULL), rc(NULL), ltag(false), rtag(false) { //有线索为true
        data = 0;
    }
}*thTree;

//线索二叉树初始化
void createthTree(thTree& th) {
    char ch;
    cin >> ch;
    if (ch == '#') th = NULL;
    else {
        if (!(th = new thNode)) exit(-1);
        th->data = ch;
        createthTree(th->lc);
        createthTree(th->rc);
    }
}

//将一棵左右链表示的二叉树线索化
//将左右链指针表示的二叉树t线索化，pre为树t根结点的中根序的直接前驱
//pre和t 的位置一直在不断的进行变动；左孩子（false）和直接前驱（true）存一，右孩子和直接后继存一。
void convert_to_thTree(thTree t, thTree& pre) {
    if (t == NULL) return;

    convert_to_thTree(t->lc, pre); // 进入左子树

    //因为已经默认ltag，rtag为false，所以可以将以下内容简写
    /*
    if (t->lc != NULL) //t的左指针域为孩子结点
        t->ltag = false;
    else //t的左指针域为线索，指向其直接前驱pre
        t->lc = pre, t->ltag = true;

    if (pre->rc != NULL)  //pre的右指针域为孩子结点
        pre->rtag = false;
    else //pre的右指针域为线索，指向其直接后继t
        pre->rtag = true, pre->rc = t;
    */

    if (t->lc == NULL) {
        t->lc = pre, t->ltag = true;
    }

    if (pre->rc == NULL) {
        pre->rtag = true;
        pre->rc = t;
    }

    pre = t; //t的右子树中根序的第一个结点的直接前驱为t
    convert_to_thTree(t->rc, pre);
}

//将左右链表示的二叉树转化为带头结点header的线索二叉树，使之可以双向操作
void thTree_create(thTree& header, thTree t) {
    if (!(header = new thNode)) exit(-1);

    if (t == NULL) {
        header->lc = header;
        return;       //若根结点不存在,则该二叉树为空,让该头结点指向自身.
    }
    //header线索的直接后继设置为header
    header->rtag =true;
    header->rc = header;
    
    thTree pre;
    //原二叉树中根序的第一个结点的直接前驱为header
    header->lc = t;
    pre = header; 

    //开始递归输入线索化
    convert_to_thTree(t, pre);
    //此时结束了最后一个结点的线索化了,下面的代码把头结点的后继指向了最后一个结点.
    //并把最后一个结点的后继也指向头结点,此时树成为了一个类似双向链表的循环.
    pre->rc = header,pre->rtag =true; pre为中根序列的最后一个节点
    header->rc = pre; //该代码删除后，为单向
    return ;
}

//基于线索二叉树的中根遍历
//该遍历方法不需要递归或其他辅助容器，可以更快的获得二叉树的中根序列。   
void thTree_midOrder(thTree header) {
    thTree p = header->lc;     
    while (p != header) {
        while (p->ltag == false) p = p->lc;    //走向左子树的尽头
        cout<<p->data<<endl;
        //此时的p为中根序列的第一个结点，后面根据线索遍历
        while (p->rtag ==true && p->rc != header) {  //访问该结点的后续结点
            p = p->rc;
            cout << p -> data<<endl;
        }
        p = p->rc;
    }
    return ;
}

//注意：学会查找左子树的最左/最右孩子，右子树的最左或最右孩子

int main() {
    thTree B, T;
    createthTree(B);
    thTree_create(T, B);
    cout<<"中序遍历二叉树的结果为："<<endl;
    thTree_midOrder(T);
    cout << endl;
}

//测试数据:ABD##EG###CF#H###