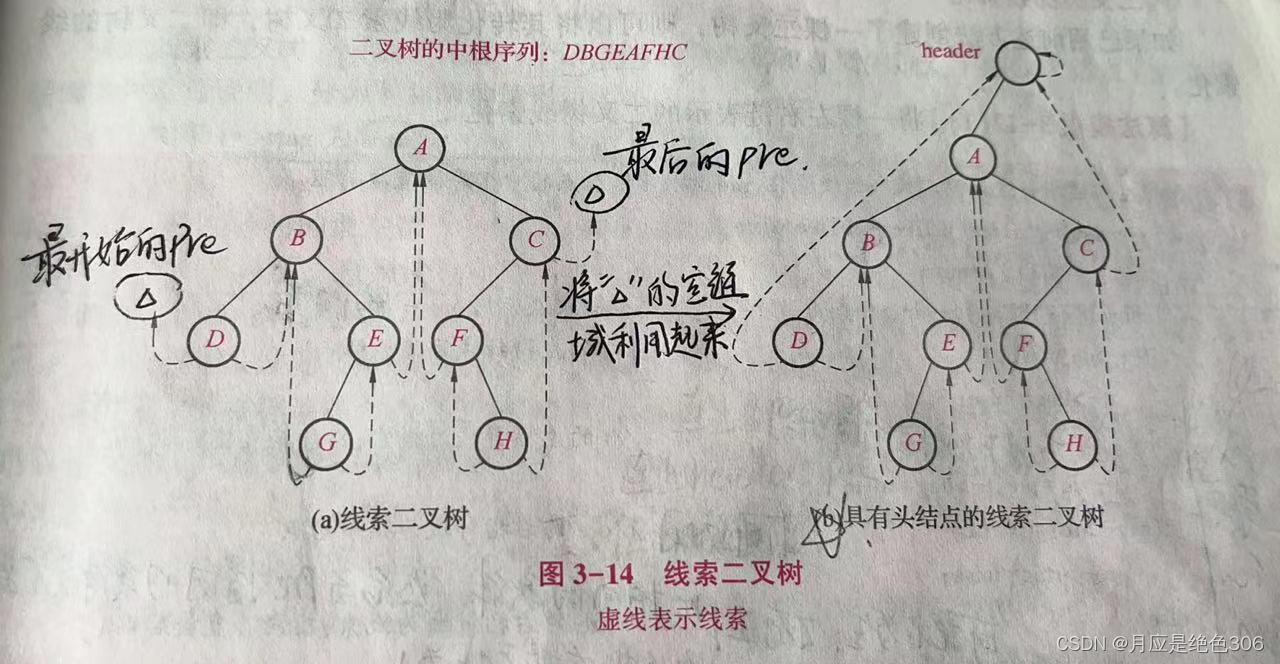
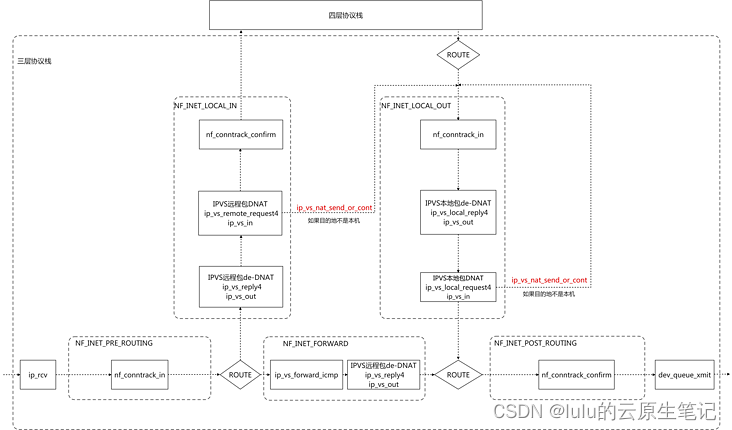
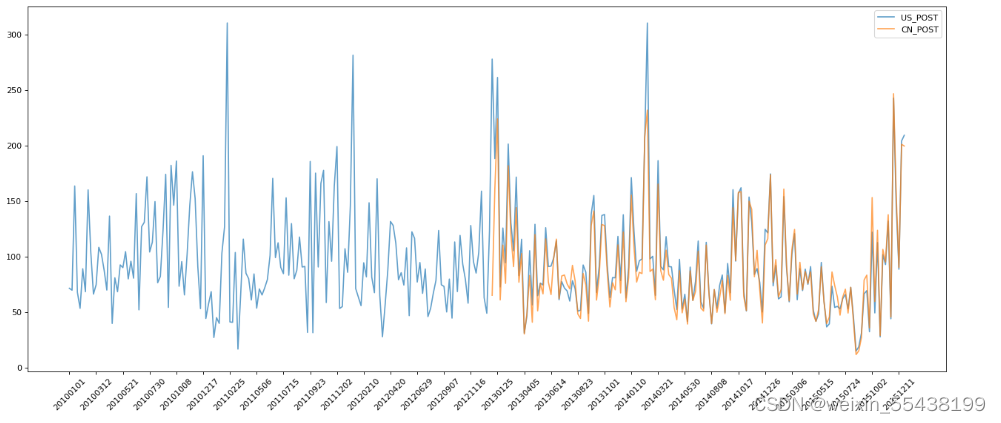
不严谨的说，时域和频域分析就是在不同的空间看待问题的，不同空间所对应的原子(基函数)是不同的。你想一下时域空间的基函数是什么？频域空间的基函数是什么？一般的时-频联合域空间的基函数是什么？小波域空间的基函数是什么？

有的空间域比较容易分析，有的空间域不容易分析。

举个例子吧，首先加载一个双曲Chirp信号，数据的采样频率为2048Hz，第一个Chirp信号持续时间为0.1~0.68秒，第二个Chirp信号持续时间为0.1~0.75 秒，第一个Chirp信号在时间t处的瞬时频率为（单位Hz）：

​

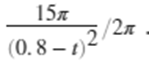
添加图片注释，不超过 140 字（可选）

第二个Chirp信号在时间t处的瞬时频率为（单位Hz）：

​

看一下从时域空间看待的时域图

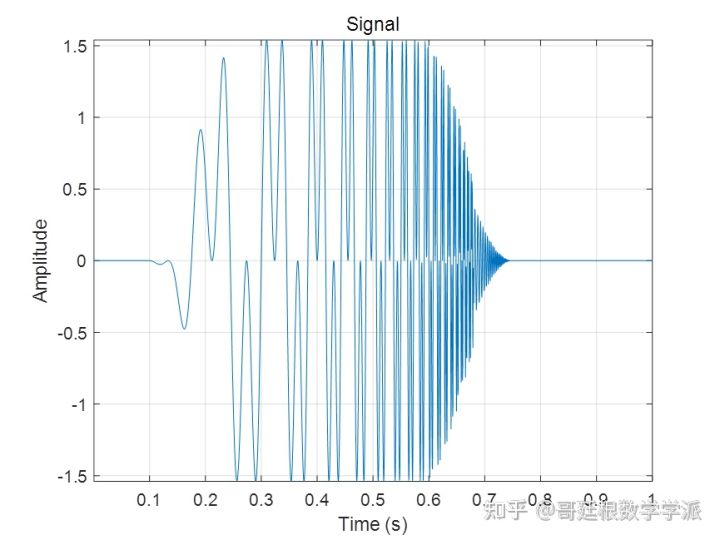
​然后看一下频域空间的频谱图 傅里叶变换（FT）比较擅长识别信号中存在的频率分量， 但是FT无法定位频率分量。绘制上面信号的幅值谱，并放大0到200Hz之间的区域

​再看一下一般的时频域空间的时频谱图，以短时傅里叶变换为例 傅里叶变换不提供时间信息，为了定位频率，短时傅里叶变换STFT方法将信号分割成不同的窗，并对每个窗执行FT。STFT的时频分析窗口如下：

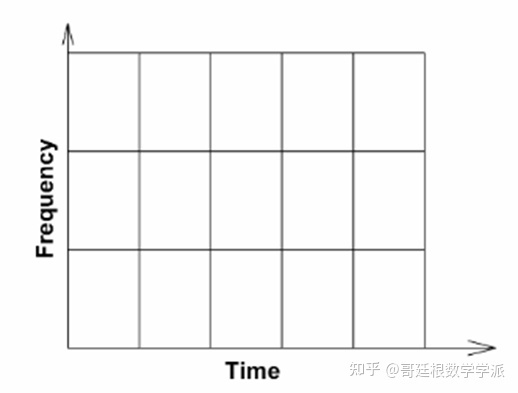
​STFT提供了信号时间-频率域中的一些信息， 但是选择窗的大小是关键。 对于STFT时频分析，选择更短的窗以牺牲频率分辨率为代价从而获得良好的时间分辨率。相反，选择较大的窗以时间分辨率为代价从而获得良好的频率分辨率（著名的测不准原理）。一旦STFT的分析窗确定后，将在整个分析中保持不变（最致命的缺陷）。以 200 毫秒的时间窗大小绘制上述双曲Chirp信号的频谱图，频谱图上的瞬时频率为黑色虚线段。

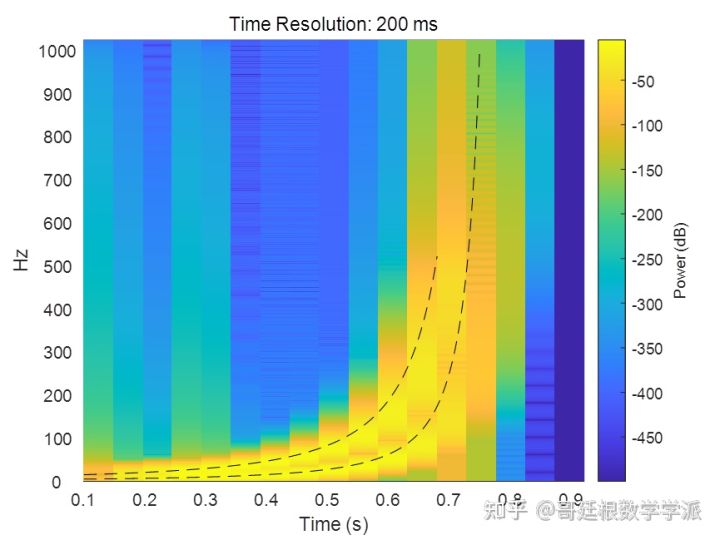
​然后绘制时间窗大小为50毫秒的频谱图

​两个图的结果是显而易见的，没有单一的窗口大小可以解析此类信号的整个频率信息。 最后看一下小波空间对应的小波时频谱图 连续小波变换 CWT是为了克服 STFT中固有的时频分辨率问题。CWT的时频分析窗口如下：

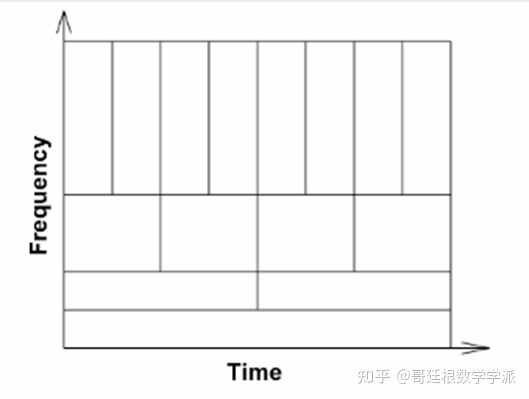
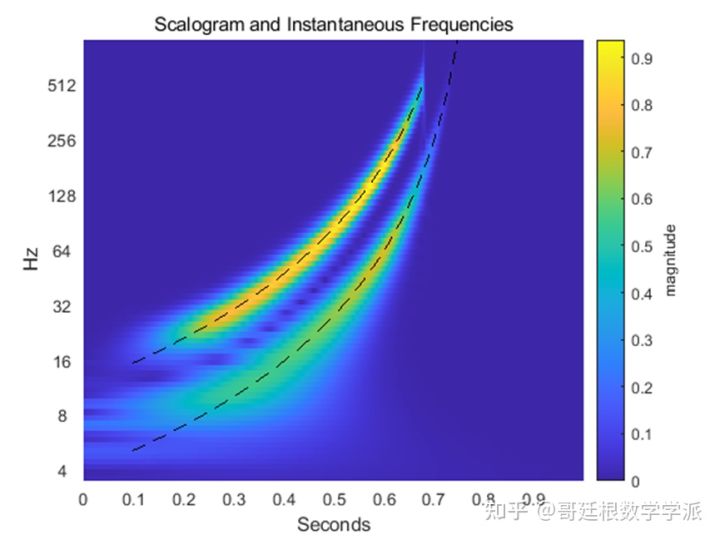
​CWT和人类的听觉系统非常一致:在低频处有更好的频率定位能力，在高频处有更好的时间定位能力。绘制 CWT时尺度谱（尺度谱是作为时间和频率绘制的 CWT的绝对值），因为CWT 中的频率是对数的，所以使用对数频率轴。

​从图中可以清楚地看出信号中两个双曲Chirp信号的存在，CWT可以比较准确估计持续时间的瞬时频率，而无需担心选择窗的大小。要了解小波系数幅度增长速度有多快，可以看一下3-D 图

​在尺度谱上绘制一下瞬时频率，可见瞬时频率与尺度谱特征非常吻合

​

从不同的空间域（角度）看待问题，分析的难度也不一样