解题思路

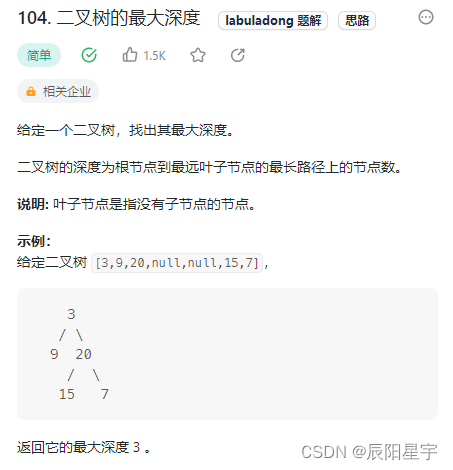
在这里插入图片描述
原题链接：104. 二叉树的最大深度

解题思路

1、迭代法：层次遍历BFS

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(!root)       return 0;
        int res = 0;
        queue<TreeNode*> que;
        que.push(root);
        while(!que.empty()) {
            int n = que.size();
            res++;
            while(n--) {
                TreeNode* node = que.front();
                que.pop();                
                if(node->left)      que.push(node->left);
                if(node->right)     que.push(node->right);
            }
        }
        return res;
    }
};

2、递归：先序遍历DFS

设置一个变量depth记录深度变化，一个变量res记录全局中最大深度。每次是先判定中间节点，再分别处理左、右子树。当中间结点为叶子结点时，判定此时是否为最大高度。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int res = 0;    
    void traversal(TreeNode* node, int &depth) {
        if(node == NULL)       return ;
        // 该层结点不为空，深度加一
        depth++;
        // 当遍历到叶结点时，计算最大高度
        if(node->left == NULL && node->right == NULL)   // 中
            res = max(res, depth);
        traversal(node->left, depth);                   // 左
        traversal(node->right, depth);                  // 右
        // 该层结点已遍历完，返回上一层，去剩余情况遍历
        depth--;
    }

    int maxDepth(TreeNode* root) {
        int depth = 0;
        traversal(root, depth);
        return res;
    }
};

3、递归：后序遍历DFS（分解问题思路）

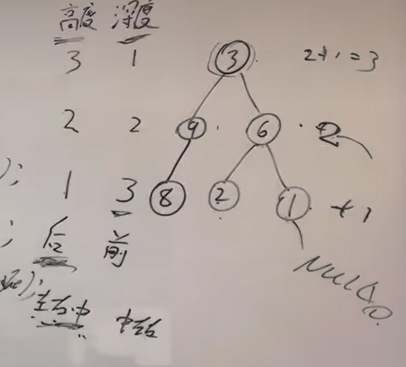
想要求出最大深度，也就是得到左子树最大深度和右子树最大深度。将该问题看作，自底向上，每次获取子树的最大深度，即可得到整个树的最大深度。

使用栈的特点，第一次执行时，会将初始函数压入栈中，最终结果的答案会在最后返回。之后子函数会不断压栈，计算最大深度，并把计算结果返回给上一次层的函数。

这个实现，实际上也就是二叉树的后序遍历，以左右中的顺序处理，每次处理完中后，即将该层的结果返回给上一层，上一层继续处理。

注意：后序遍历实际上求得是最大高度。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(root == NULL)    return 0;
        int maxLeft = maxDepth(root->left);     // 左
        int maxRight = maxDepth(root->right);   // 右
        return max(maxLeft, maxRight) + 1;      // 中，处理完后，交给上一层处理
    }
};