导读
大多数关于假设检验的教程都是从先验分布假设开始,列出一些定义和公式,然后直接应用它们来解决问题。然而,在本教程[1]中,我们将从第一原则中学习。这将是一个示例驱动的教程,我们从一个基本示例开始,逐步了解假设检验的内容。
1. 选哪个骰子?

想象一下,您面前有两个无法区分的骰子。您随机选择一个骰子并扔掉它。在观察它落在哪张面上之后,您能确定您选择了哪个骰子吗?
骰子的概率分布如下图所示:
Die 1:
P(X=x) = 1/6 if x = {1, 2, 3, 4, 5, 6}
Die 2:
P(X=x) = 1/4 if x = {1, 2}
= 1/8 if x = {3, 4, 5, 6}
在二元假设检验问题中,我们通常会面临两个我们称之为假设的选择,我们必须决定是选择一个还是另一个。
假设由 H₀ 和 H₁ 表示,分别称为原假设和备择假设。在假设检验中,我们拒绝或接受零假设。
在我们的示例中,骰子 1 和骰子 2 分别是原假设和备择假设。接受或拒绝零假设的决定取决于观察的分布。
所以我们可以说假设检验的目标是画一个边界,把观察空间分成两个区域:拒绝区域和接受区域。
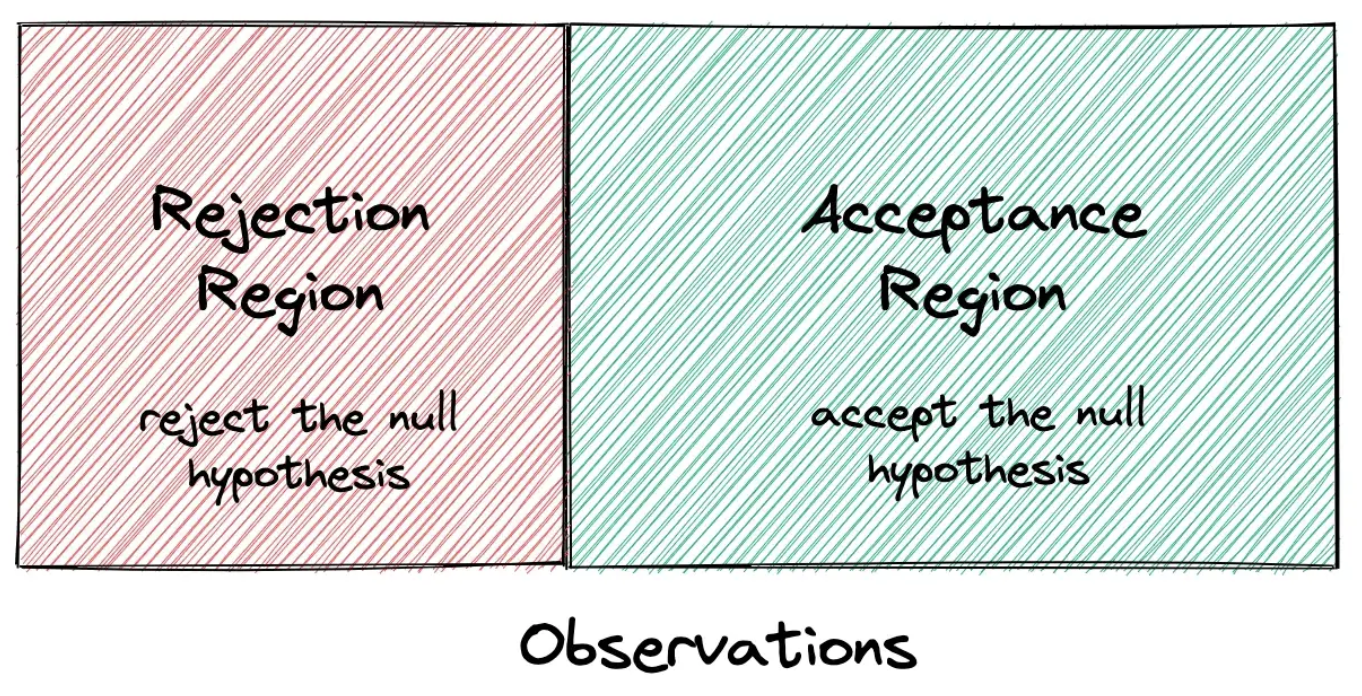
如果落在拒绝区域,我们拒绝原假设,否则我们接受它。现在,决策边界不会是完美的,我们会犯错误。例如,骰子 1 可能落在骰子 1 或 2 上,而我们将其误认为是骰子 2;但发生这种情况的可能性较小。我们将在下一节中学习如何计算错误概率。
我们如何确定决策边界?有一种简单有效的方法称为似然比检验,我们接下来将讨论。
2. 似然比检验
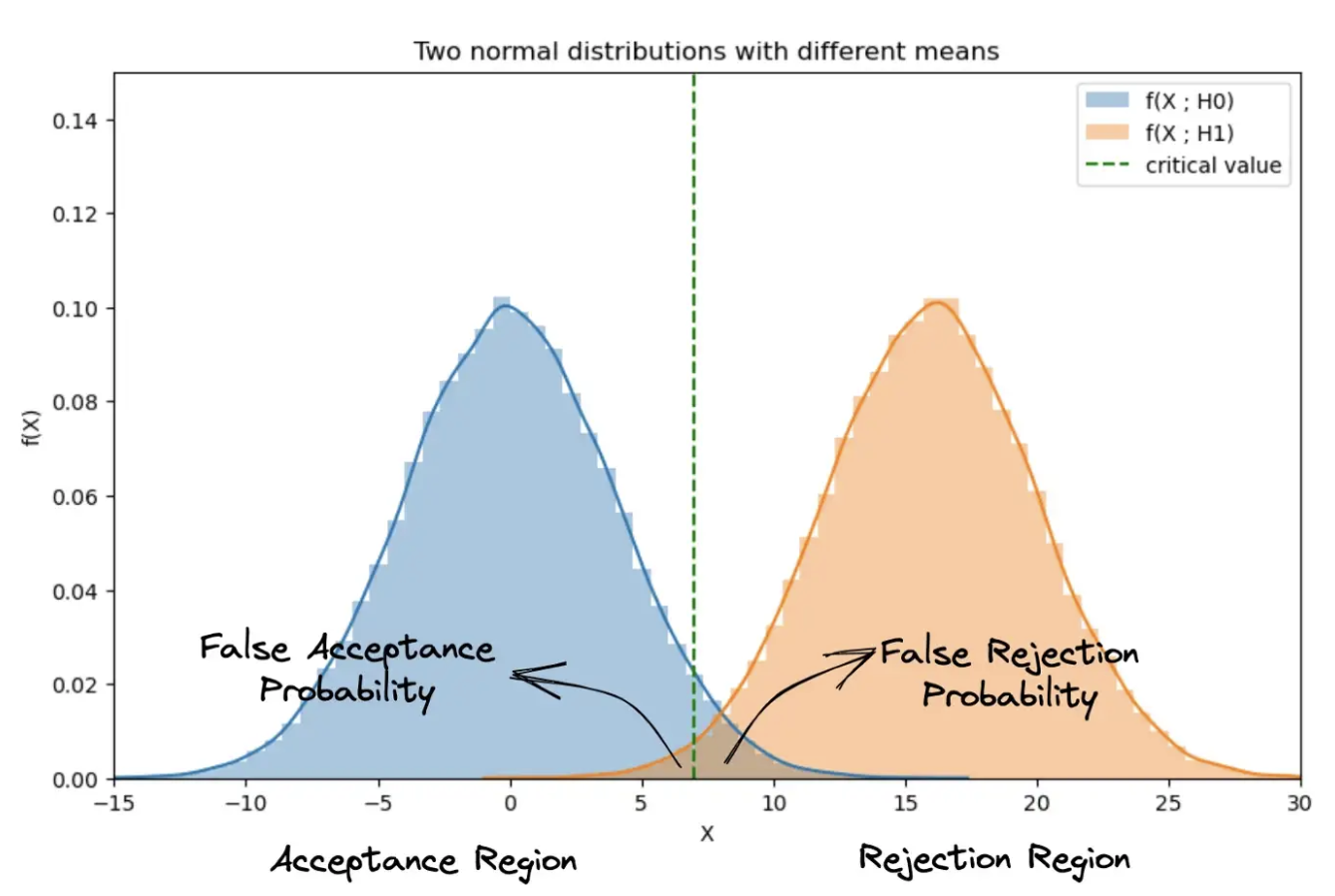
你必须首先意识到观察的分布取决于假设。下面我根据两个假设绘制了示例中的分布:
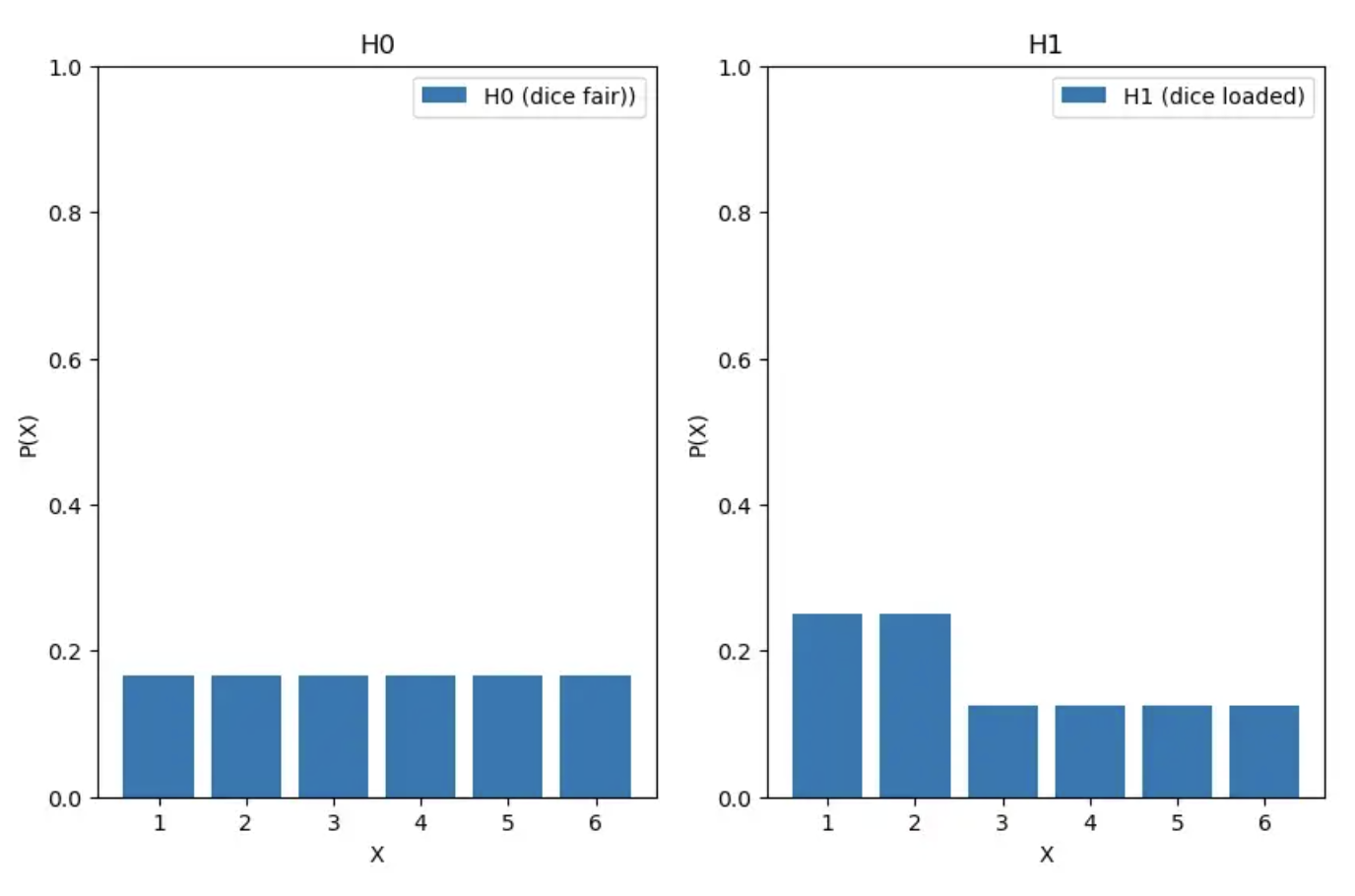
现在,P(X=x;H₀) 和 P(X=x;H₁) 分别表示在假设 H₀ 和 H₁ 下观察的可能性。它们的比率告诉我们,对于不同的观察,一个假设比另一个假设正确的可能性有多大。
这个比率称为似然比,用 L(X) 表示。 L(X) 是依赖于观察值 x 的随机变量。
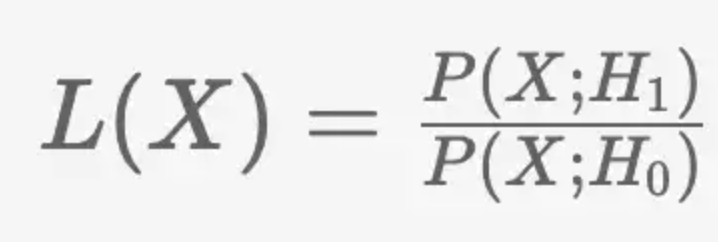
在似然比检验中,如果该比率高于某个值,我们拒绝原假设,即如果 L(X) > 𝜉 则拒绝原假设,否则接受它。称为临界比。
因此,这就是我们绘制决策边界的方法:我们将似然比大于临界比的观察值与似然比大于临界值的观察值分开。
所以形式为 x 落入拒绝域,其余落入接受域。
让我们用我们的骰子例子来说明它。似然比可以计算为:
L(X) = (1/4) / (1/6) = 3/2 if x = {1, 2}
= (1/8) / (1/6) = 3/4 if x = {3, 4, 5, 6}
似然比图如下所示:
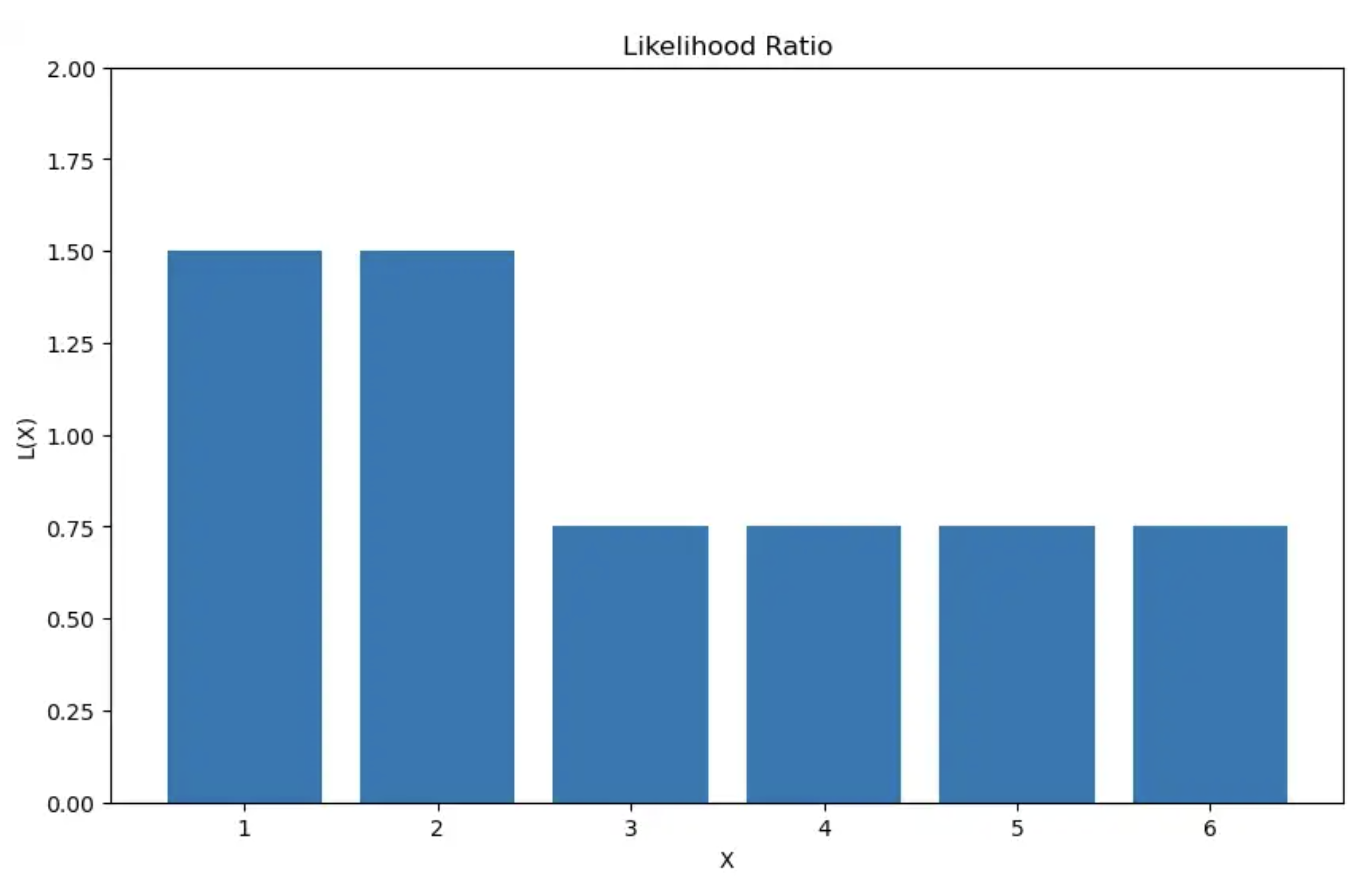
现在决策边界的放置归结为选择临界比率。假设临界比率是 3/2 和 3/4 之间的值,即 3/4 < 𝜉 < 3/2。然后我们的决策边界看起来像这样:
if 3/4 < 𝜉 < 3/2:
L(X) > 𝜉 if x = {1, 2} (rejection region)
L(X) < 𝜉 if x = {3, 4, 5, 6} (acceptance region)
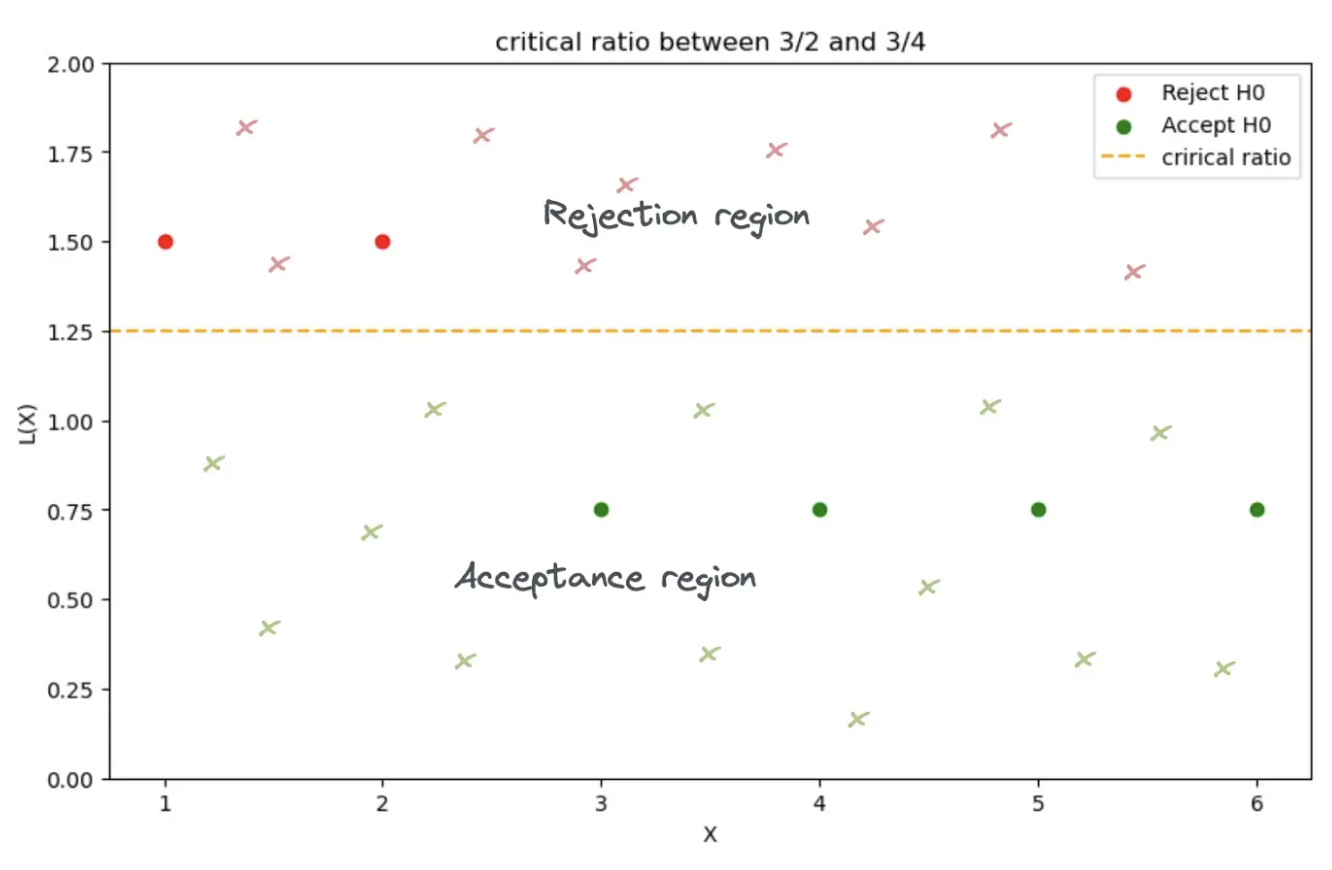
让我们讨论与此决定相关的错误。如果观察 x 属于拒绝区域但发生在零假设下,则会发生第一类错误。在我们的示例中,这意味着骰子 1 落在 1 或 2 上。
这称为错误拒绝错误或类型 1 错误。此错误的概率由下式表示并且可以计算为:
False Rejection Error:
𝛼 = P(X|L(X) > 𝜉 ; H₀)
如果观察 x 属于接受区域但发生在备择假设下,则会发生第二个错误。这称为错误接受错误或类型 2 错误。此错误的概率由下式表示并且可以计算为:
False Acceptance Error:
𝛽 = P(X|L(X) < 𝜉 ; H₁)
在我们的示例中,错误拒绝和错误接受错误可以计算为:
Computing errors in the dice example:
𝛼 = P(X|L(X) > 𝜉 ; H₀)
= P(X={1, 2} ; H₀)
= 2 * 1/6
= 1/3
𝛽 = P(X|L(X) < 𝜉 ; H₁)
= P(X={3, 4, 5, 6} ; H₁)
= 4 * 1/8
= 1/2
让我们考虑另外两种情况,其中临界比率采用以下值:𝜉 > 3/2 和 𝜉 < 3/4。
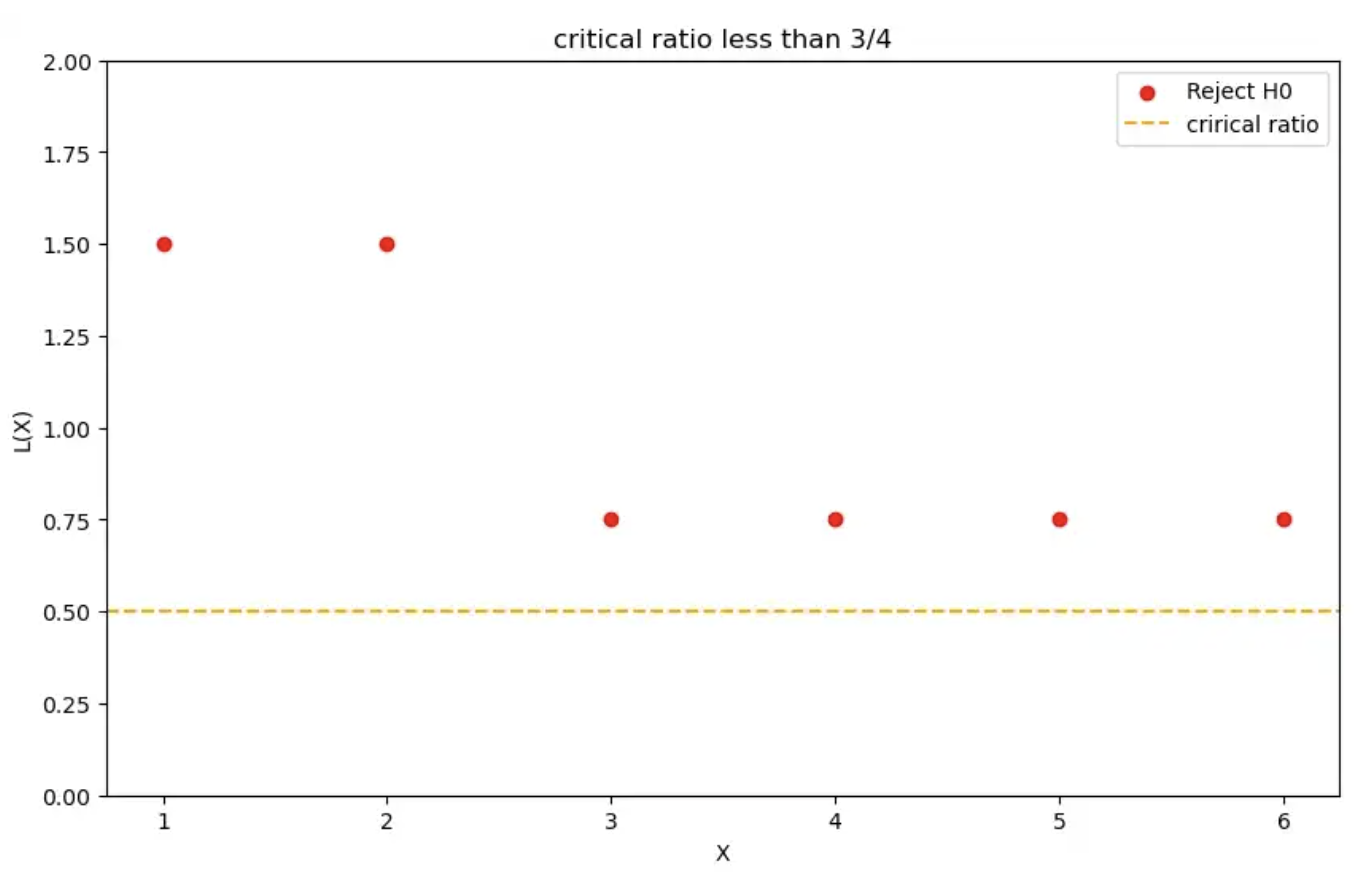
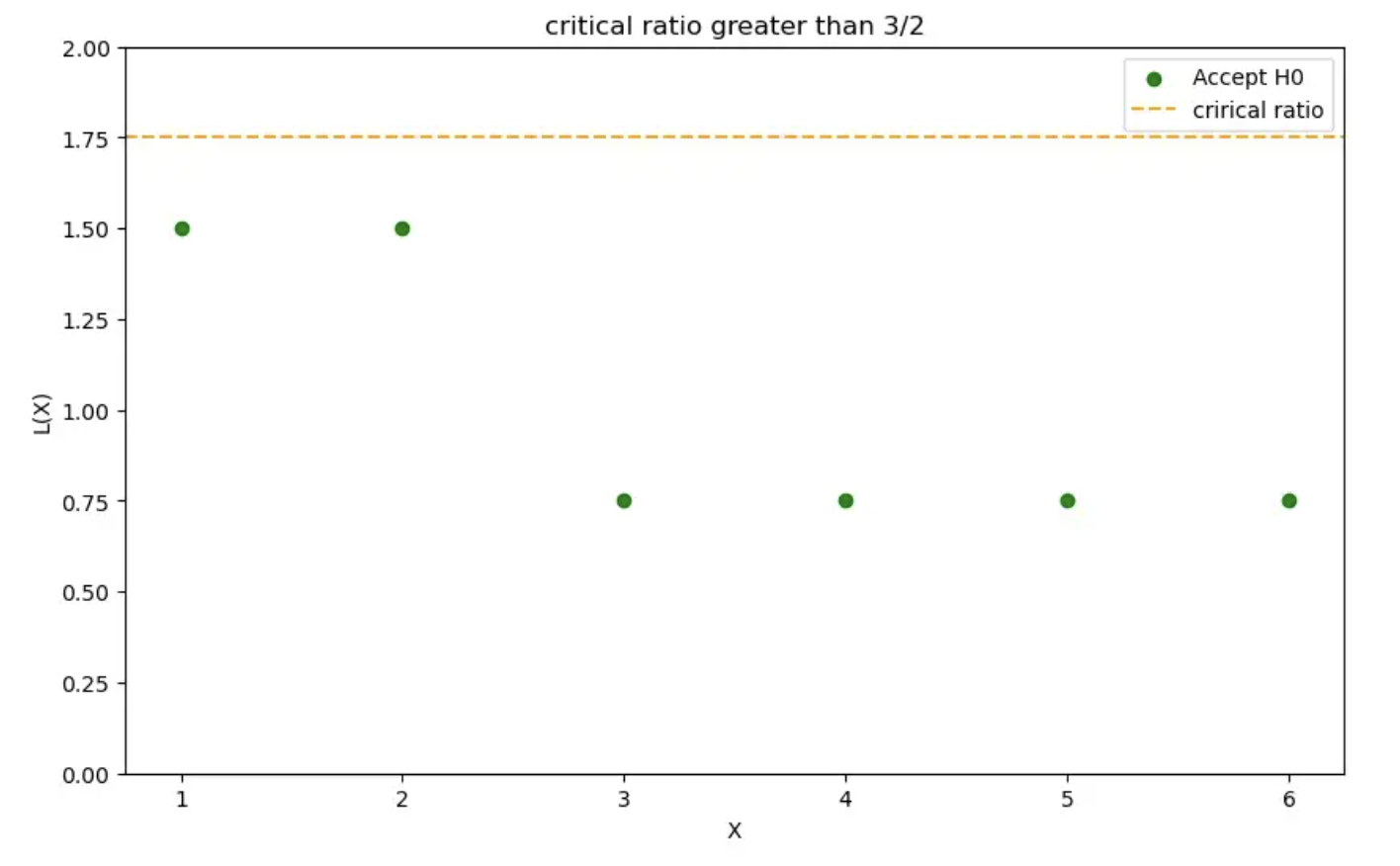
可以类似地计算类型 1 和类型 2 错误。
𝛼 = 0 if 𝜉 > 3/2
= 1/3 if 3/4 < 𝜉 < 3/2
= 1 if 𝜉 < 3/4
𝛽 = 1 if 𝜉 > 3/2
= 1/2 if 3/4 < 𝜉 < 3/2
= 0 if 𝜉 < 3/4
让我们绘制不同 𝜉 值的误差。
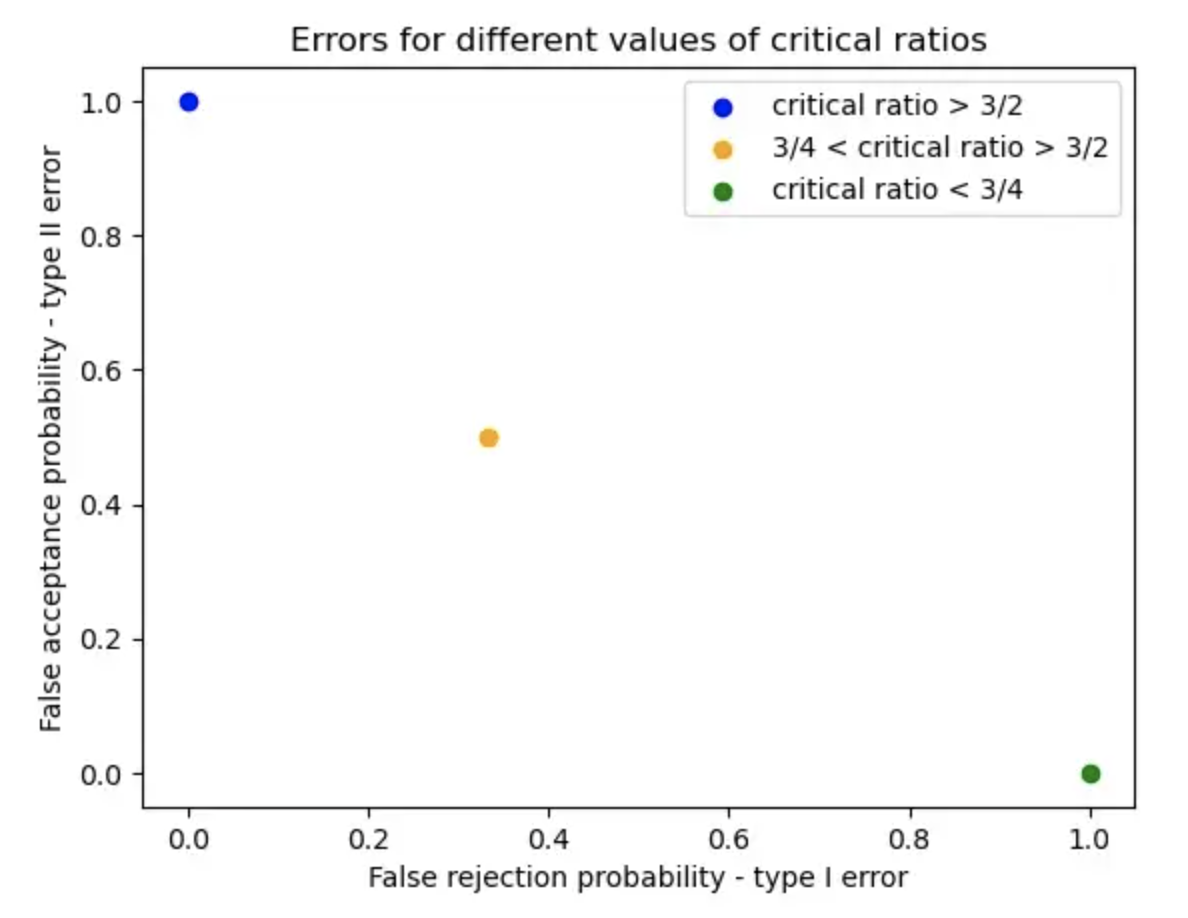
随着临界值的增加,拒绝域变小。结果,错误拒绝概率降低,而错误接受概率增加。
3. 似然比的作用
我们可以在观察空间的任何地方画出边界。为什么我们需要计算似然比并通过所有这些?
下面我计算了不同边界的 I 类和 II 类错误。
Type I and Type II errors for different boundaries.
'|' is the separator - {rejection region | acceptance region}
1. {|, 1, 2, 3, 4, 5, 6}
𝛼 = P(x={} ; H₀) = 0
𝛽 = P(x={1, 2, 3, 4, 5, 6} ; H₁) = 1
𝛼 + 𝛽 = 1
2. {1, |, 2, 3, 4, 5, 6}
𝛼 = P(x={1} ; H₀) = 1/6
𝛽 = P(x={2, 3, 4, 5, 6} ; H₁) = 1/4 + 1/2 = 3/4
𝛼 + 𝛽 = 0.916
3. {1, 2, |, 3, 4, 5, 6}
𝛼 = P(x={1, 2} ; H₀) = 1/3
𝛽 = P(x={3, 4, 5, 6} ; H₁) = 1/2
𝛼 + 𝛽 = 0.833
4. {1, 2, 3, |, 4, 5, 6}
𝛼 = P(x={1, 2, 3} ; H₀) = 1/2
𝛽 = P(x={4, 5, 6} ; H₁) = 3/8
𝛼 + 𝛽 = 0.875
5. {1, 2, 3, 4, |, 5, 6}
𝛼 = P(x={1, 2, 3, 4} ; H₀) = 2/3
𝛽 = P(x={5, 6} ; H₁) = 1/4
𝛼 + 𝛽 = 0.916
6. {1, 2, 3, 4, 5, |, 6}
𝛼 = P(x={1, 2, 3, 4, 5} ; H₀) = 5/6
𝛽 = P(x={6} ; H₁) = 1/8
𝛼 + 𝛽 = 0.958
6. {1, 2, 3, 4, 5, 6, |}
𝛼 = P(x={1, 2, 3, 4, 5, 6} ; H₀) = 1
𝛽 = P(x={} ; H₁) = 0
𝛼 + 𝛽 = 1
I 类和 II 类错误及其不同边界总和的图如下所示:
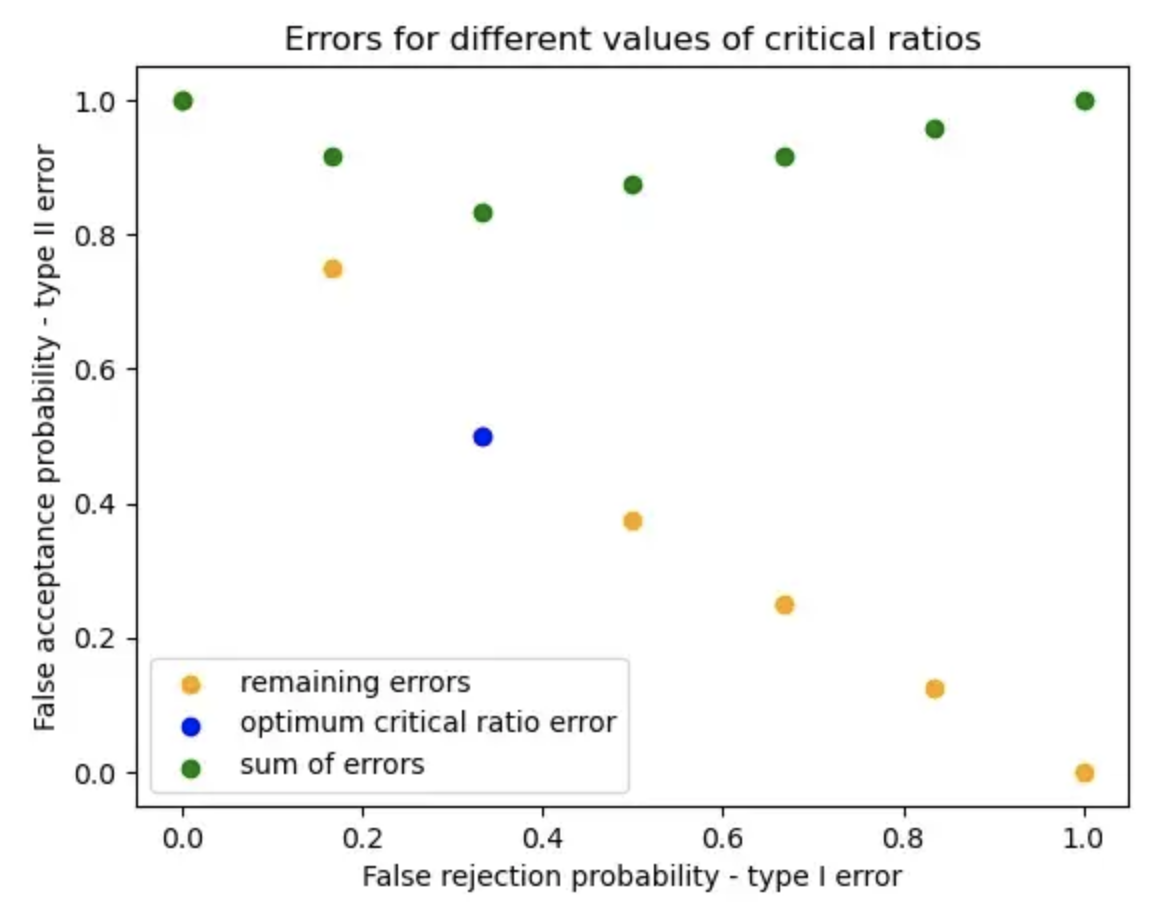
可以看出,对于似然比检验得到的临界比值的最优值,Ⅰ类和Ⅱ类错误之和最小。
换句话说,对于给定的错误拒绝概率,似然比检验提供了最小可能的错误接受概率。
4. 连续分布
在上面的例子中,我们没有讨论如何选择临界比的值。概率分布是离散的,因此临界比率的微小变化不会影响边界。
当我们处理连续分布时,我们固定错误拒绝概率的值并据此计算临界比率。
P(L(X) > 𝜉 ; H₀) = 𝛼
但同样,过程将是相同的。一旦我们获得临界比率的值,我们就分离观察空间。
𝛼的典型选择是 𝛼 = 0.01、𝛼 = 0.05 或 𝛼 = 0.01,具体取决于错误拒绝的不良程度。
例如,如果我们正在处理正态分布,我们可以对其进行标准化并查找 Z 表以找到给定的值。
总结
在本文中,我们了解了假设检验背后的概念和过程。整个过程可以总结为下图:

我们从两个假设 H₀ 和 H₁ 开始,使得基础数据的分布取决于假设。目标是通过找到将观察值 x 的已实现值映射到两个假设之一的决策规则来证明或反驳原假设 H₀。最后,我们计算与决策规则相关的误差。
欢迎Star -> 学习目录
参考资料
Source: https://towardsdatascience.com/introduction-to-hypothesis-testing-with-examples-60a618fb1799
本文由 mdnice 多平台发布