拓扑排序

有向无环图一定是拓扑序列,有向有环图一定不是拓扑序列。

无向图没有拓扑序列。

首先我们先来解释一下什么是有向无环图：

有向就是我们两个结点之间的边是有方向的，无环的意思就是整个序列中没有几个结点通过边形成一个圆环。

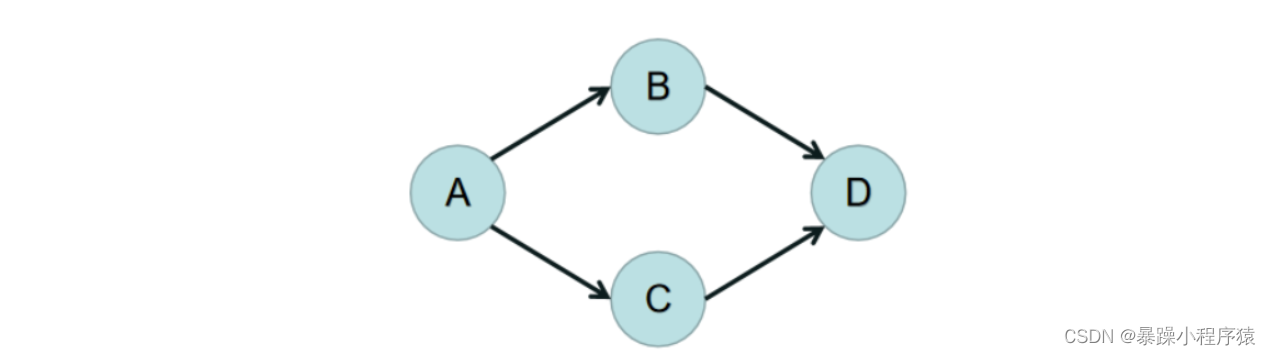
下图就是一个有向无环图，它也一定是拓扑序列。

下图就是有向有环图：

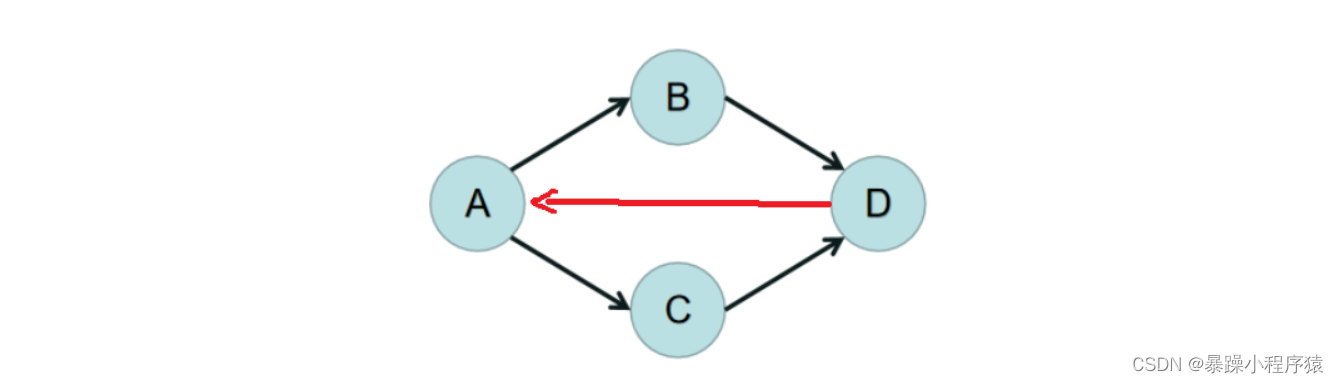
拓扑序列：

首先我们引入度的概念：

对于有向图每个结点都有入度和出度，入度就是指向该结点的边数，出度就是该结点指向其他结点的边数。

如第一个图：

A的入度为0，出度为2；

B的入度为1，出度为1；

C的入度为1，出度为1；

D的入度为2，出度为0；

总结一下拓扑排序就是只有从前指向后的边，没有从后指向前的边。

如果是一个有向无环图，那么一定有一个点的入度为0，如果找不到一个入度为0的点，这个图一定是带环的。

拓扑排序满足：每条边(x,y)，x在序列中都在y前面。

拓扑排序的思路：

一个有向图，如果图中有入度为 0 的点，就把这个点删掉，同时也删掉这个点所连的边。

一直进行上面出处理，如果所有点都能被删掉，则这个图可以进行拓扑排序。

我们画图来解释一下：

首先我们的有向无环图是这样的：

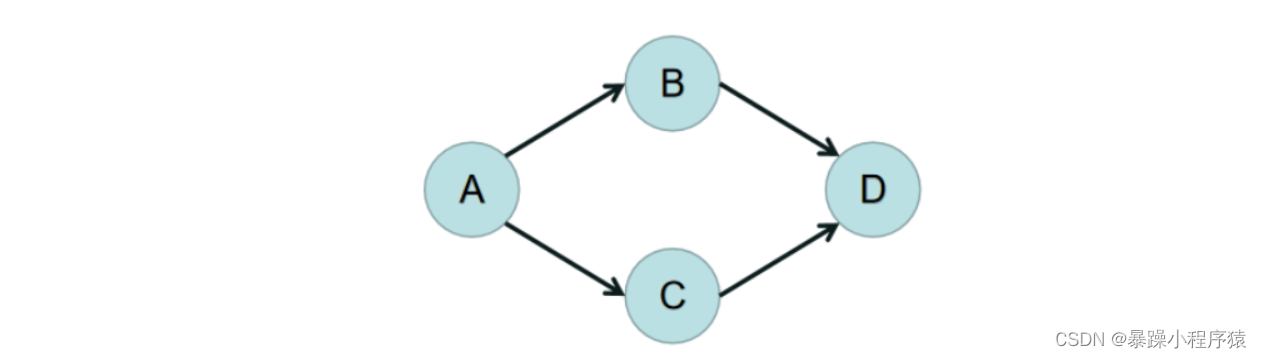
我们发现A的入度为0，那么A就可以作为源点（不会有边在它前面），然后删除A和A上所连的边，如下图：

然后我们发现B和C的入度都是0，那么同样删除B，C和B，C上所连的边，如下图：

然后D的入度为0，我们同样操作，最后图被删除干净，证明可以拓扑排序。

解题思路

首先记录各个点的入度

然后将入度为 0 的点放入队列

将队列里的点依次出队列，然后找出所有出队列这个点发出的边，删除边，同时边的另一侧的点的入度 -1。

如果所有点都进过队列，则可以拓扑排序，输出所有顶点。否则输出-1，代表不可以进行拓扑排序。

我们先来看一下拓扑排序的模板：

时间复杂度 O(n+m), n表示点数，m表示边数。

bool topsort()
{
    int hh = 0, tt = -1;

    // d[i] 存储点i的入度
    for (int i = 1; i <= n; i ++ )
        if (!d[i])
            q[ ++ tt] = i;

    while (hh <= tt)
    {
        int t = q[hh ++ ];

        for (int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (-- d[j] == 0)
                q[ ++ tt] = j;
        }
    }

    // 如果所有点都入队了，说明存在拓扑序列；否则不存在拓扑序列。
    return tt == n - 1;
}

我们来看一下练习题：

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=1e5+10;
int h[N],e[N],ne[N],idx; //邻接表存储图
int n,m; //n个点，m个边
int q[N],d[N];//q表示队列,d表示点的入度
void add(int a,int b)
{
    e[idx]=b;
    ne[idx]=h[a];
    h[a]=idx++;
}
bool topsort()
{
    int hh=0,tt=-1;
    for(int i=1;i<=n;i++)
    {
        if(!d[i])//如果i这个点的入度为0，那么我们就入队
        q[++tt]=i;
    }
        while(hh<=tt) //如果队列不为空
        {
            int t=q[hh++];//用t来接收队头的元素，同时队头指针hh++；
            for(int i=h[t];i!=-1;i=ne[i])//我们来从t结点开始遍历它的边
            {
                int j=e[i];//t有一条边指向j
                d[j]--;//删除掉t指向j的这条边，j的入度-1；
                if(d[j]==0) //如果j的入度为0，那么我们就将j入队
                q[++tt]=j;
            }
        }
    
    return tt==n-1;
     //表示如果n个点都入队了话,那么该图为拓扑图,返回true,否则返回false
     //我们的tt初始值是-1，当插入一个值的时候tt先++在插入，所以我们一个有n个结点，全部入队的话tt指针应该是n-1；
}
int main()
{
    cin>>n>>m;//保存点的个数和边的个数
    memset(h,-1,sizeof(h));//初始化邻接表
    for(int i=0;i<m;i++)//我们一共有m个边，所以我们循环插入边
    {
        int a,b;
        scanf("%d%d",&a,&b);
        add(a,b);
        d[b]++;//插入的边是由a指向b的，所以b的入度++；
    }
    if(topsort())
    {
        for(int i=0;i<n;i++) 
        printf("%d ",q[i]);
        puts("");
    }
    else
    puts("-1");
    return 0;
    
}