linux学习：栈（汉诺塔游戏）

news2024/11/26 12:42:50

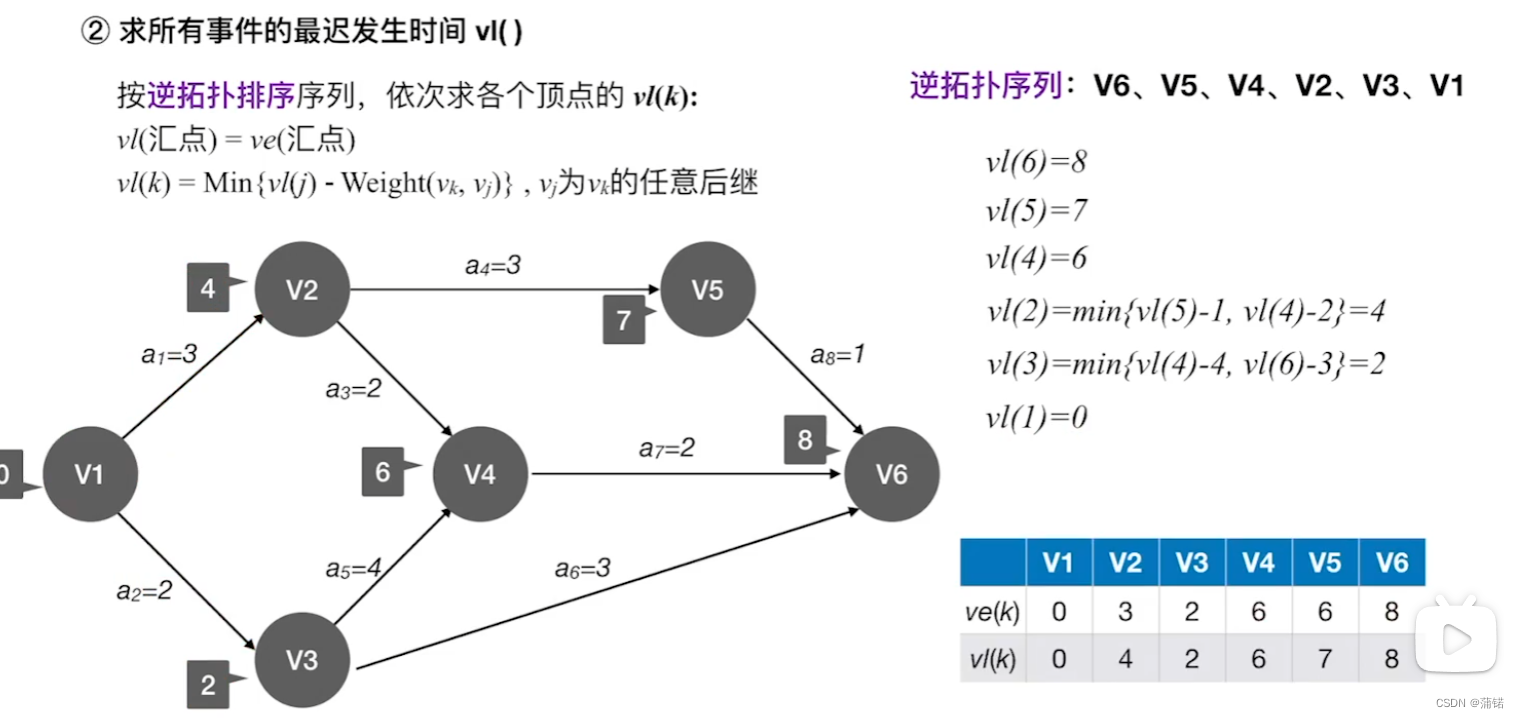
第一根上面套着 64 个圆的金片，最大的一个在底下，其余一个比一个小，依次叠上去，庙里的众僧不倦地把它们一个个地从这根棒搬到另一根棒上，规定可利用中间的一根棒作为帮助，但每次只能搬一个，而且大的不能放在小的上面。

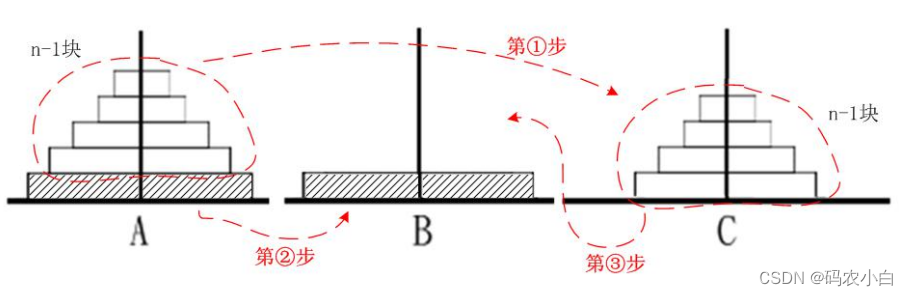
每次只能拿最上面的一个，然后放的时候也必须放到最上面，这个逻辑其实就是栈。再要解决这个问题，可以将这个问题“递归化”：假设有 n 个汉诺塔在 A 号柱子上，那么解题的步骤是：

第①步：将 A 上面的 n-1 个汉诺塔先搬到 C 上。
第②步：直接将 A 最底下的那块汉诺塔出栈，然后直接在 B 上压栈。
第③步：再把那 n-1个汉诺塔从 C 搬到 B 上。

1 #include <stdio.h>
2 #include <unistd.h>
3 #include <stdlib.h>
4 #include <stdbool.h>
5
6 struct node // 链式栈节点
7 {
8     int data;
9     struct node *next;
10 };
11
12 struct linked_stack // 链式栈的管理结构体
13 {
14     struct node *top; // 栈顶元素指针
15     int size; // 当前栈元素总数
16 };
17
18 struct linked_stack *s1, *s2, *s3; // 定义成全局变量是为了方便打印
19
20 bool stack_empty(struct linked_stack *s) // 判断栈是否为空
21 {
22     return s->size == 0;
23 }
24
25 struct node *new_node(int data) // 创建一个新的节点
26 {
27     struct node *new = malloc(sizeof(struct node));
28     if(new != NULL)
29     {
30         new->data = data;
31         new->next = NULL;
32     }
33     return new;
34 }
35 // 将新节点 new 压入栈 s 中
36 bool push(struct linked_stack *s, struct node *new)
37 {
38     if(new == NULL)
39         return false;
40
41     new->next = s->top;
42     s->top = new;
43     s->size++;
44
45     return true;
46 }
47 // 从栈 s 中取出栈顶元素
48 bool pop(struct linked_stack *s, struct node **p)
49 {
50     if(stack_empty(s))
51         return false;
52
53     *p = s->top;
54     s->top = s->top->next;
55     (*p)->next = NULL;
56     s->size--;
57
58     return true;
59 }
60
61 void show(struct linked_stack *s1, 
62     struct linked_stack *s2, 
63     struct linked_stack *s3) // 纵向同时显示三个链栈数据
64 {
65     int maxlen, len;
66
67     maxlen = s1->size > s2->size ? s1->size : s2->size;
68     maxlen = maxlen > s3->size ? maxlen : s3->size;
69     len = maxlen;
70
71     struct node *tmp1 = s1->top;
72     struct node *tmp2 = s2->top;
73     struct node *tmp3 = s3->top;
74
75     int i;
76     for(i=0; i<maxlen; i++)
77     {
78         if(tmp1 != NULL && len <= s1->size)
79         {
80             printf("%d", tmp1->data);
81             tmp1 = tmp1->next;
82         }
83         printf("\t");
84
85         if(tmp2 != NULL && len <= s2->size)
86         {
87             printf("%d", tmp2->data);
88             tmp2 = tmp2->next;
89         }
90         printf("\t");
91
92         if(tmp3 != NULL && len <= s3->size)
93         {
94             printf("%d", tmp3->data);
95             tmp3 = tmp3->next;
96         }
97         printf("\n");
98
99         len--;
100     }
101     printf("s1\ts2\ts3\n-----------------\n");
102 }
103
104 void hanoi(int n, struct linked_stack *ss1, 
105     struct linked_stack *ss2, 
106     struct linked_stack *ss3)
107 {
108     if(n <= 0)
109         return;
110
111     struct node *tmp;
112
113     hanoi(n-1, ss1, ss3, ss2); // 第①步：将 n-1 个汉诺塔从 s1 移到 s3
114     getchar();
115     show(s1, s2, s3);
116     pop(ss1, &tmp);// 第②步：将最底层汉诺塔从 s1 移动到 s2
117     push(ss2, tmp);
118     hanoi(n-1, ss3, ss2, ss1); // 第③步：将 n-1 个汉诺塔从 s3 移到 s2
119 }
120 // 初始化一个空的链栈
121 struct linked_stack *init_stack(void)
122 {
123     struct linked_stack *s;
124     s = malloc(sizeof(struct linked_stack)); // 申请链栈管理结构体
125
126     if(s != NULL)
127     {
128         s->top = NULL;
129         s->size = 0;
130     }
131     return s;
132 }
133
134 int main(void)
135 {
136     printf("how many hanois ? ");
137     int hanois;
138     scanf("%d", &hanois);
139
140     s1 = init_stack(); // 初始化三个链栈，用来表示三根金刚石柱子
141     s2 = init_stack();
142     s3 = init_stack();
143
144     int i;
145     for(i=0; i<hanois; i++) // 在第一个栈中压入 n 个数，代表汉诺塔
146     {
147         struct node *new = new_node(hanois-i);
148         push(s1, new);
149     }
150
151     hanoi(hanois, s1, s2, s3); // 使用递归算法移动这些汉诺塔
152     show(s1, s2, s3); // 显示移动之后的汉诺塔形状
153
154     return 0;
155 }