“合并K个升序链表”，这是一道中等难度的题目，经常出现在编程面试中。以下是该问题的详细描述、解题步骤、不同算法的比较、代码示例及其分析。

问题描述

给你一个链表数组，每个链表都已经按升序排列。

请你将所有链表合并到一个升序链表中，返回合并后的链表。

示例：

输入：lists = [[1,4,5],[1,3,4],[2,6]]

输出：[1,1,2,3,4,4,5,6]

解释：链表数组如下：

[
  1->4->5,
  1->3->4,
  2->6
]

将它们合并到一个有序链表中得到。

1->1->2->3->4->4->5->6

方法一：直接合并

解题步骤

1. 初始化：
   • 如果链表数组为空，则返回None。
   • 如果链表数组中只有一个链表，则直接返回这个链表。
2. 逐对合并链表：
   • 初始化merged_list为lists[0]，即从第一个链表开始。
   • 逐个遍历余下的链表，与merged_list进行合并，每次合并后更新merged_list。
3. 合并两个链表的函数：
   • 创建一个哑结点dummy作为合并链表的起始节点。
   • 使用两个指针分别指向两个链表的头部，比较指针所指节点的值，将较小值节点连接到结果链表上，然后移动该指针到下一个节点。
   • 如果某一链表遍历完毕，将另一链表的剩余部分直接连接到结果链表的尾部。
   • 返回哑结点的下一个节点，即合并后链表的头部。
4. 完成合并：
   • 继续遍历并合并剩余的链表，直至所有链表均合并完成。

代码示例

class ListNode:
    def __init__(self, val=0, next=None):
        self.val = val
        self.next = next

def mergeTwoLists(l1: ListNode, l2: ListNode) -> ListNode:
    dummy = ListNode(0)
    current = dummy
    
    while l1 and l2:
        if l1.val < l2.val:
            current.next = l1
            l1 = l1.next
        else:
            current.next = l2
            l2 = l2.next
        current = current.next
    
    # Attach the remaining part of l1 or l2
    current.next = l1 if l1 is not None else l2
    return dummy.next

def mergeKLists(lists: List[Optional[ListNode]]) -> Optional[ListNode]:
    if not lists:
        return None
    if len(lists) == 1:
        return lists[0]
    
    merged_list = lists[0]
    for i in range(1, len(lists)):
        merged_list = mergeTwoLists(merged_list, lists[i])
    
    return merged_list

性能分析

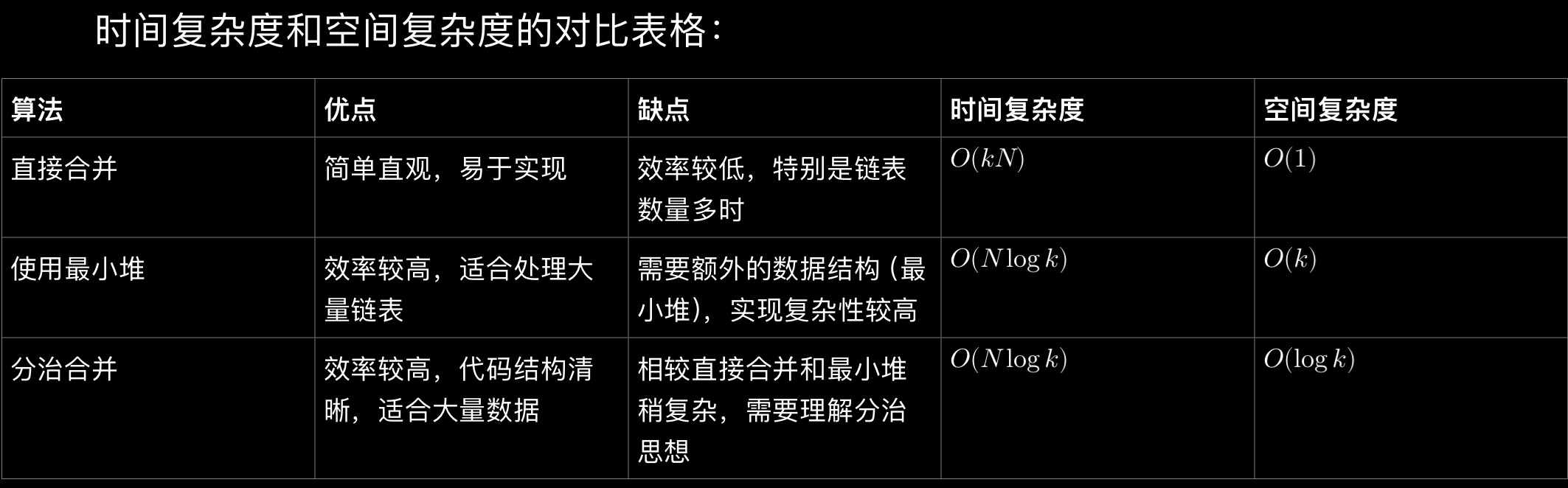
时间复杂度：对于k个链表的情况，直接合并的时间复杂度是O(kN)，其中N是链表中的节点总数。这是因为每次合并操作需要遍历涉及的两个链表的长度，而链表长度随着合并次数增加而增长。
空间复杂度：O(1)，不计入输入和输出占用的空间，合并过程中只使用了常数额外空间。

结论

直接合并是一个简单直观的方法，适合链表数量较少或对时间复杂度要求不是非常严格的情况。然而，对于大量链表的合并，使用最小堆或分治法（如两两合并）可能会更高效。

方法二：使用最小堆

解题步骤

1. 初始化最小堆：
   • 创建一个空的最小堆（优先队列）来存储链表节点，堆中的元素按节点的值排序。
   • 遍历所有链表，将每个链表的头节点加入最小堆中。
2. 构建结果链表：
   • 创建一个哑结点（dummy node）作为结果链表的头部，这样可以方便地添加新节点。
   • 使用一个指针current跟踪结果链表的最后一个节点。
3. 遍历并合并：
   • 当最小堆不为空时，执行以下操作：
   • 从堆中弹出最小元素（当前最小节点）。
   • 将current的next指针指向这个最小节点。
   • 移动current指针到最小节点。
   • 如果这个最小节点有后继节点，则将后继节点加入最小堆中。
4. 完成合并：
   • 当最小堆为空时，所有链表的节点都已链接到结果链表中。
   • 返回哑结点的next，即合并后链表的头部。

代码示例

import heapq

class ListNode:
    def __init__(self, val=0, next=None):
        self.val = val
        self.next = next

def mergeKLists(lists):
    if not lists:
        return None

    # Create a heap and a dummy node to start the merged list
    heap = []
    dummy = ListNode(0)
    current = dummy

    # Initial population of the heap with the first node of each list, if available
    for i, node in enumerate(lists):
        if node:
            heapq.heappush(heap, (node.val, i, node))

    # Iterate over the heap and build the merged list
    while heap:
        val, idx, node = heapq.heappop(heap)
        current.next = node
        current = current.next
        if node.next:
            heapq.heappush(heap, (node.next.val, idx, node.next))

    return dummy.next

性能分析

时间复杂度：每个节点被处理一次，而且每次处理涉及的时间复杂度为O(log k)，因此总的时间复杂度是O(Nlogk)，其中是所有链表中元素的总数，是链表的数量。
空间复杂度：最小堆中最多存储个元素，因此空间复杂度是O(k)。

结论

使用最小堆的方法在合并多个链表时非常有效，尤其是当链表数量较多时。这种方法的时间复杂度相对较低，是因为它能快速地找到当前最小的节点并将其加入到结果链表中，而空间复杂度则主要由堆的大小决定。这使得最小堆方法在处理大规模数据时表现出色。

方法三：分治合并

解题步骤

1. 递归分治函数定义：
   • 创建一个函数mergeKLists，如果列表为空或长度为1，直接返回。
   • 如果列表长度大于1，将链表列表分成两半，分别对这两半递归调用mergeKLists。
2. 合并两个链表的函数：
   • 创建另一个辅助函数mergeTwoLists用于合并两个链表。这个函数将两个链表头作为输入，合并后返回新链表的头。
3. 执行分治合并：
   • 在mergeKLists中，通过递归地将链表数组拆分至只剩单个链表，然后开始合并。
   • 使用mergeTwoLists逐对合并链表，直至整个数组合并为一个链表。
4. 返回结果：
   • 递归完全执行完毕后，返回合并后的链表头部。

代码示例

class ListNode:
    def __init__(self, val=0, next=None):
        self.val = val
        self.next = next

def mergeTwoLists(l1: ListNode, l2: ListNode) -> ListNode:
    if not l1 or not l2:
        return l1 or l2
    dummy = ListNode(0)
    current = dummy
    while l1 and l2:
        if l1.val < l2.val:
            current.next = l1
            l1 = l1.next
        else:
            current.next = l2
            l2 = l2.next
        current = current.next
    current.next = l1 or l2
    return dummy.next

def mergeKLists(lists: List[ListNode]) -> ListNode:
    if not lists:
        return None
    if len(lists) == 1:
        return lists[0]
    mid = len(lists) // 2
    left = mergeKLists(lists[:mid])
    right = mergeKLists(lists[mid:])
    return mergeTwoLists(left, right)

性能分析

时间复杂度：
• 每次合并操作需要线性时间，即O(n)，其中n是参与合并的两个链表的总节点数。
• 通过每次递归减半链表数组的长度，整体上每层递归需要O(N)时间，其中N是所有链表中元素的总数。
• 递归的深度是O(log k)，因此总的时间复杂度是O(N logk)。
空间复杂度：
• 递归调用栈的深度为O(logk)，因此空间复杂度为O(logk)。

结论

分治合并是解决合并多个链表的问题中非常有效的方法，尤其适合处理大量链表的情况。它的时间复杂度与使用最小堆的方法相同，但通常在实际应用中由于常数因子较小而表现更优。此外，分治法的代码结构清晰，易于理解和实现，使其成为面试和实际工程中的常用策略。

总结

合并 K 个升序链表可以通过多种算法实现，包括直接合并、使用最小堆和分治合并。在面试中，根据具体情况选择最适合的方法。其中，使用最小堆和分治合并的方法因其较优的时间复杂度通常更受青睐。这些方法不仅展示了数据结构的有效使用，也体现了分治策略在实际问题中的应用。