目录
一、基因遗传名词解释
二、什么叫显性遗传和隐性遗传?
三、如何确定遗传性质呢?是显性还是隐性?
四、常规例子1:
五、常规例子2:
六、实际案例:
七、思考题:
八、参考:
九、使用工具:
一、基因遗传名词解释
遗传基因即 DNA,控制着遗传后代的表现特征,成对出现且微观层面为双螺旋链状结构。
人类有 23 对共 46 条染色体。其中有一对染色体控制着性别,男为 xy,女为 xx。其他 22 对共 44 条染色体为常染色体,即普通的染色体。
遗传分为 2 种性质和 3 种位置:
2 种性质:显性遗传,隐性遗传。
3 种位置:常染色体遗传,伴 x 遗传,伴 y 遗传。
二、什么叫显性遗传和隐性遗传?
显性遗传:如果某个体的一对基因中,只要出现了某个基因(比如:A),就显病。比如:AA、Aa 都显病,其中 A 为致病基因,a 为正常的等位基因。
可以比喻一锅粥,只要有一粒老鼠屎,这锅粥就变坏了。
隐性遗传:和显性遗传刚好相反。如果某个体的一对基因中,只有全是某个基因(比如:a),才显病。比如:aa,其中 a 为致病基因,A 为正常的等位基因。
可以比喻一锅粥,只要有一些米就叫粥,一粒米都没有就不能叫粥了。
三、如何确定遗传性质呢?是显性还是隐性?
记住一句口诀:无中生有则为隐,有中生无则为显。
详细解释:
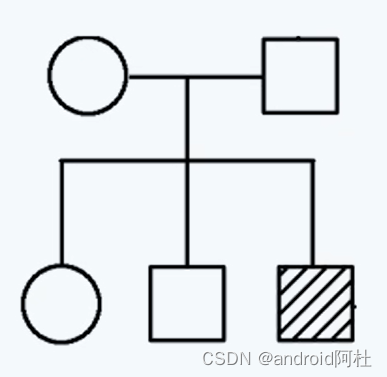
如果父母双方都没有表现病状,但是生出了有病的子或女,那就一定是隐性遗传。
图1
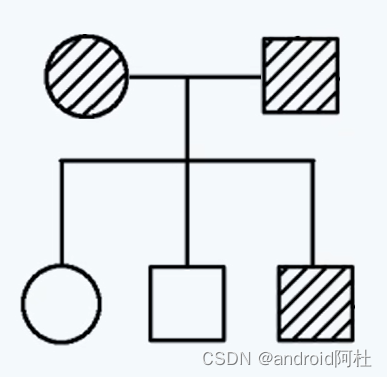
如果父母双方都表现了病状,但是生出了没有病的子或女,那就一定是显性遗传。
图2
确定了显、隐性后,如何确定是哪个位置的遗传呢?
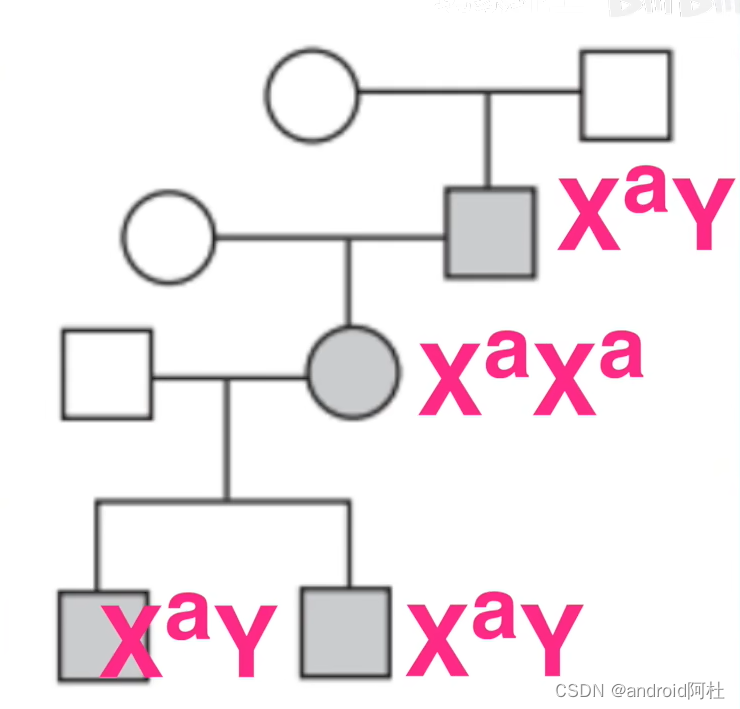
如果确定了该患者为隐性遗传,那就在该家族中寻找女患者,判断该女子的父亲和所有儿子后代是否都患病。如果是,则该病为伴 x 隐性遗传;否则为常染色体隐性遗传。
图3
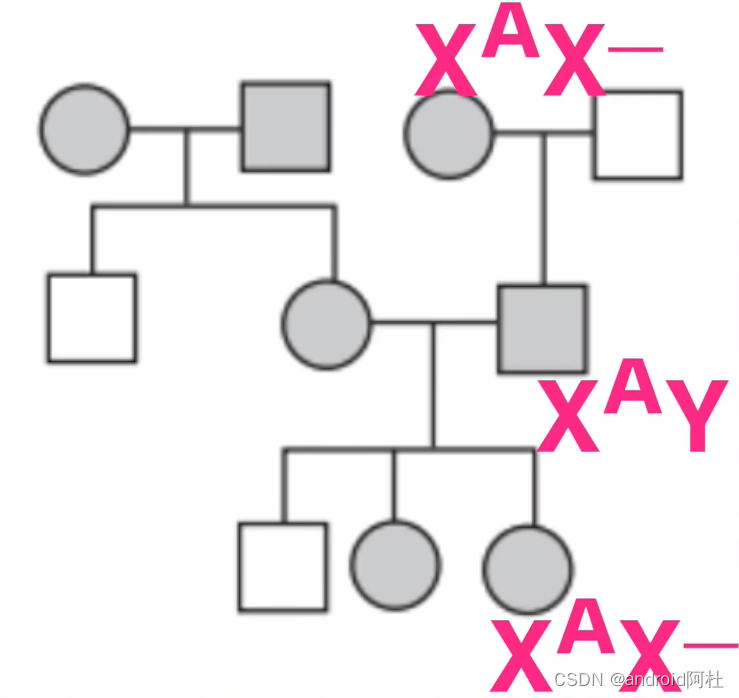
如果确定了该患者为显性遗传,那就在该家族中寻找男患者,判断该男子的母亲和所有女儿是否都患病。如果是,则该病为伴 x 显性遗传;否则为常染色体显性遗传。
图4
如果是家族中男性患病,且是代代连续相传,那就是伴 y 遗传。
一般情况下,
一个基因是常染色体显性遗传,以大写字母标记。
比如:A(取别的字母也可以,随意,但最好不要用 X 和 Y,容易混淆伴性遗传)。那患病的个体基因组成为 AA、Aa。
一个基因是常染色体隐性遗传,以小写字母标记。
比如:a(取别的字母也可以,随意,但最好不要用 x 和 y,容易混淆伴性遗传)。那患病的个体基因组成为 aa。
四、常规例子1:
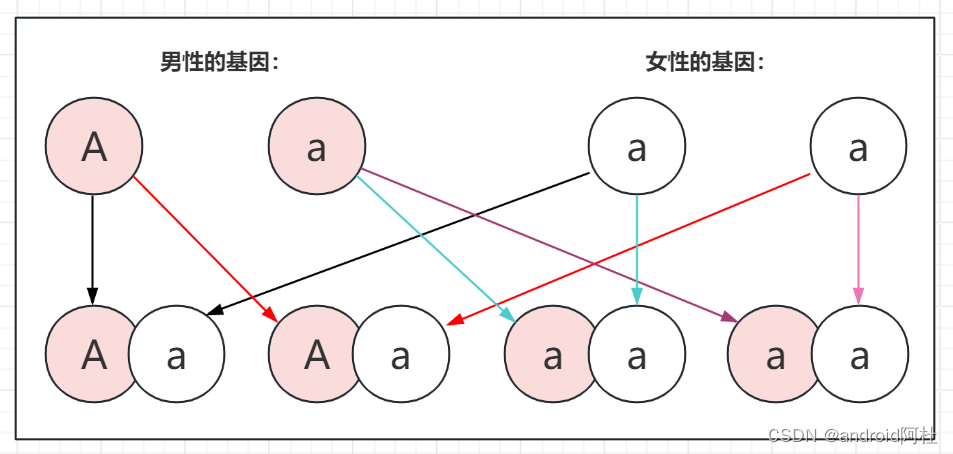
如果一个有常染色体显性遗传的男患者(Aa),与一个健康的异性结婚,生育的子女患病的数据是怎么样的?
分析:
男患者的基因:Aa。女性健康,则基因为:aa(由于 A 是显性,即只要含有 A 就患病,所有健康的女性基因只能是 aa)。
打散后自由交叉组合为:Aa Aa aa aa,即 50% 的患病孩子 Aa,50% 健康的孩子 aa。
图5
五、常规例子2:
如果一个有常染色体隐性遗传的男患者(aa),与一个健康但携带的异性结婚,生育的子女患病的数据是怎么样的?
分析:
隐性遗传,只有 aa 显病,AA、Aa 都不显病。所以:
男性患者基因:aa。健康但携带女性基因:Aa。
打散后自由交叉组合为:Aa Aa aa aa,即 50% 的健康但携带致病基因的孩子 Aa,50% 的患病的孩子 aa。
六、实际案例:
小明患有一种疾病,他是全家族中(父亲、母亲两边亲属分支上下查找多代)唯一一个患者。
那么小明和一个健康且不携带的女子结婚,生育的后代患病概率是怎么样的?
分析:
小明是全家族唯一的患者,那他的父亲、母亲不患病,符合无中生有,则是隐性遗传。
确定了是隐形遗传,再找女性患者。但是没有女性患者,那就不是伴 x 隐性遗传,也不是伴 y 遗传。
所以确定了,小明所患的疾病为常染色体隐性遗传。
所以确定小明的患病基因为:aa(也可以用别的小写字母代替)。
小明的两个 a,一个一定是来自父亲,另一个来自母亲,小明父母又是健康的。所以小明父母的基因为:Aa,Aa。
小明基因:aa。另一个健康且不携带的女性:AA。
打散后自由交叉组合为:Aa Aa Aa Aa,即全是 100% 的健康但携带致病基因的孩子 Aa。
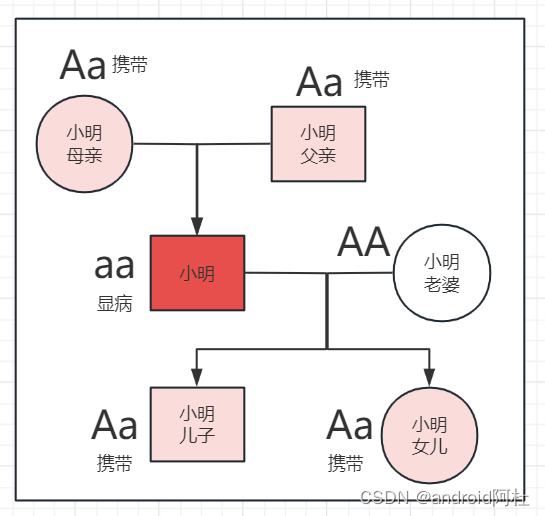
画一下小明家的基因遗传图:
图6
七、思考题:
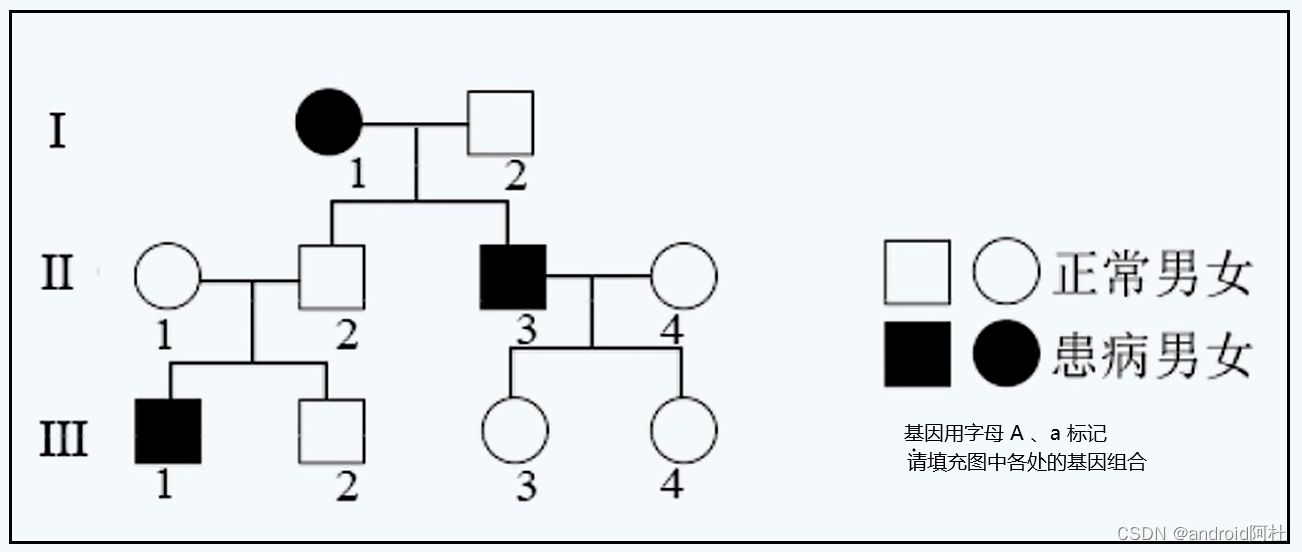
了解了以上知识,你可以填充下图中各处的基因组合吗?
图7
若文章中有错误描述或结论,欢迎评论正确的内容。感谢!
八、参考:
https://www.bilibili.com/video/BV1sE411s7uh/?spm_id_from=333.788&vd_source=cb6af91ff4f75ca79f764ed8f999786f
https://www.bilibili.com/video/BV1fa4y1F7oC?p=5&vd_source=cb6af91ff4f75ca79f764ed8f999786f
九、使用工具:
https://www.processon.com/