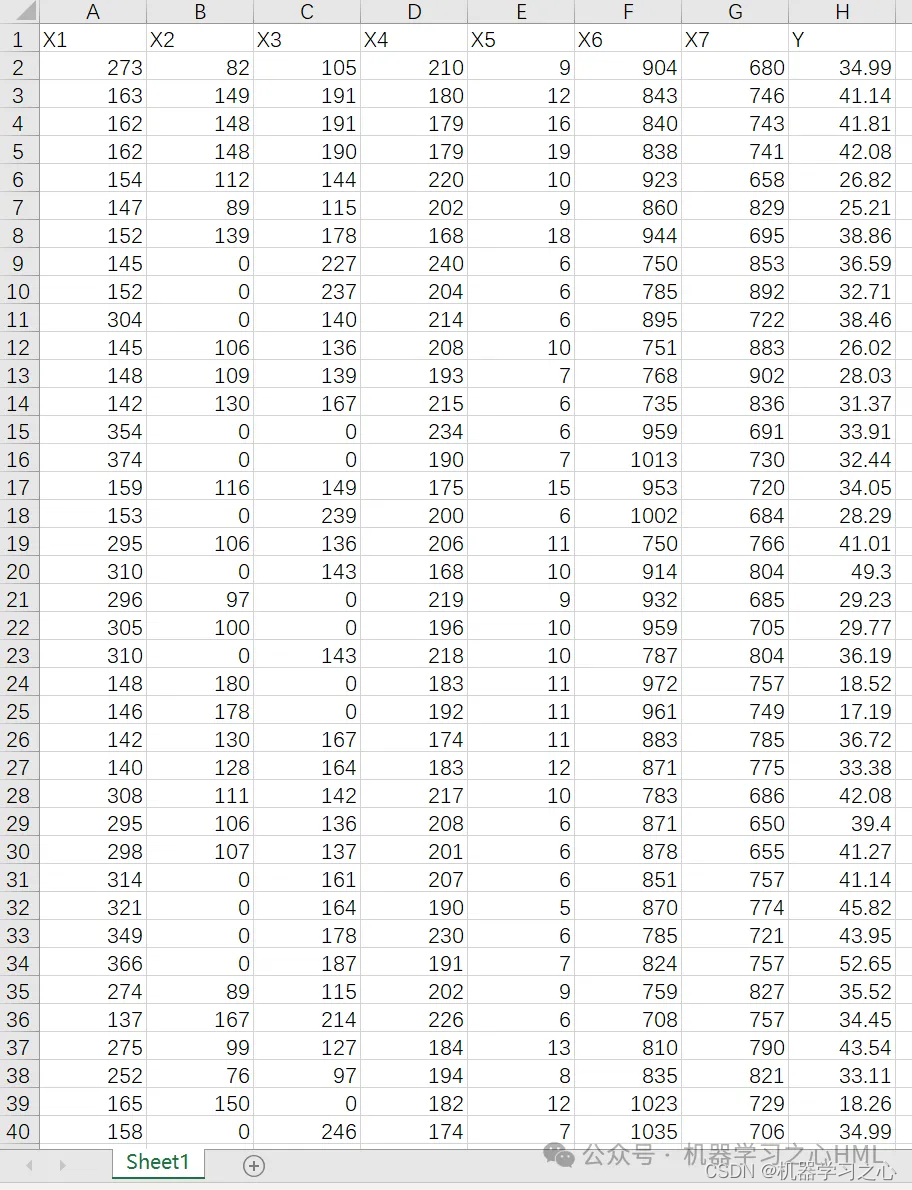
目录
前言
AOE网
AOE网的两个性质:
AOE网的五个时间
事件的最早发生时间Ve[k]
活动的最早开始时间E[i]
事件的最迟发生时间Vl[k]
活动的最晚开始时间L[i]
活动的时间余量
关于关键路径的缩短
代码实现思路
前言
本博客是博主用于复习数据结构以及算法的博客,如果疏忽出现错误,还望各位指正。
AOE网
AOE网是Activity On Edge Network,活动在路径上的图。
AOE网更多的是关心整个工程完成的最短时间是多少,哪些活动的延期将会影响整个工程的进度,而加速这些活动是否会提高整个工程的效率。
AOE网的两个性质:
- 只有再某个顶点所代表的事情发生后,从该顶点出发的各有向边所代表的活动才能开始。
- 只有在进入到某个顶点的各有向边所代表的活动都已经结束,该顶点所代表的事儿才能开始。
通俗地来讲,就是事儿办完了下一个活动才能开始,活动办完了下一个事儿才能开始。
同时,在AOE网中仅有一个入度为0的顶点,称为开始顶点(源点)。
也仅有一个出度为0的顶点,称为结束顶点(汇点),它表示整个工程的结束。
AOE网的五个时间
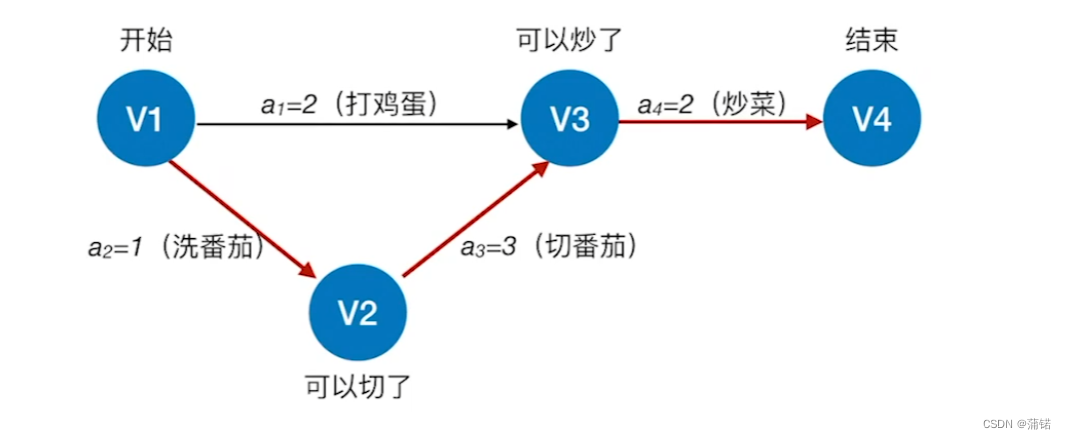
就拿王道举的例子,做一道西红柿炒鸡蛋来讲。
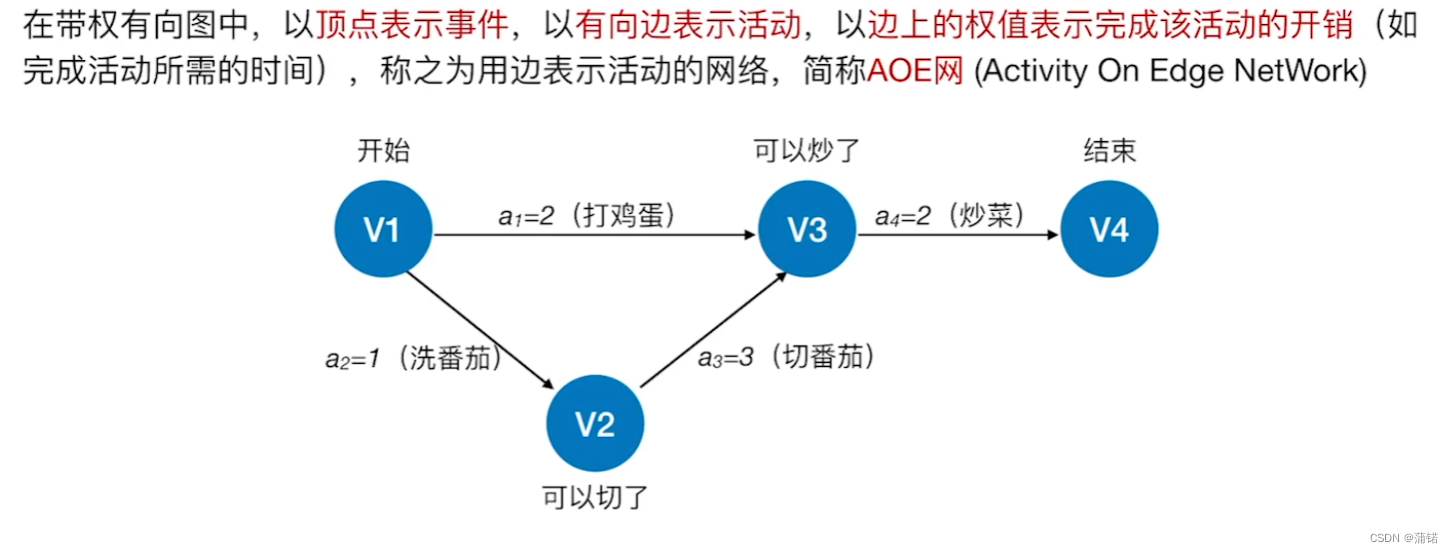
从源点到汇点的有向路径可能有多条,所有路径中,具有最大路径长度的路径称为关键路径,而把关键路径上的活动称为关键活动。
完成整个工程的最短时间就是关键路径的长度,若关键活动不能按时完成,则整个工程的完成时间就会延长。
对于AOE网,仍采用邻接表存储。
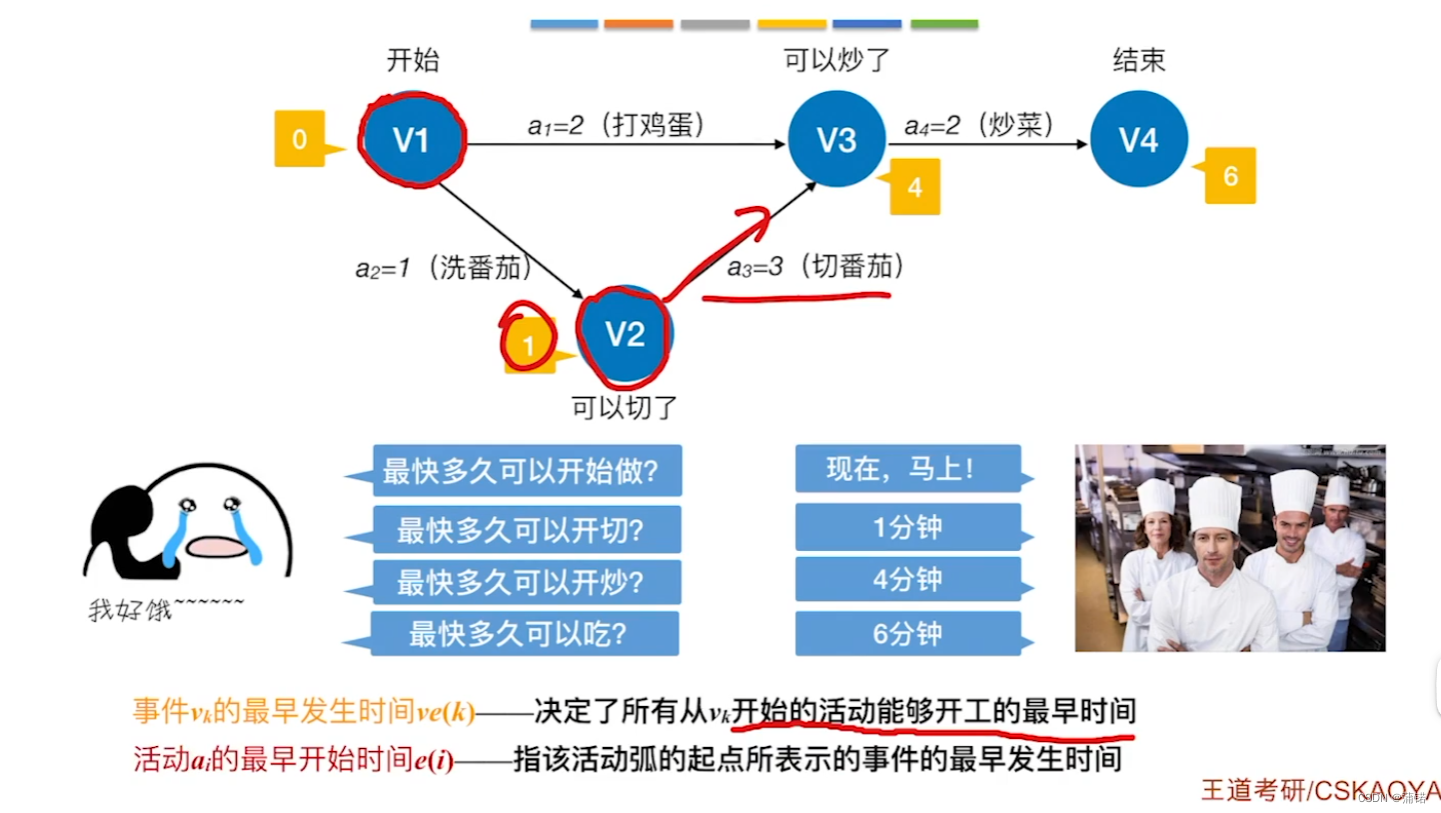
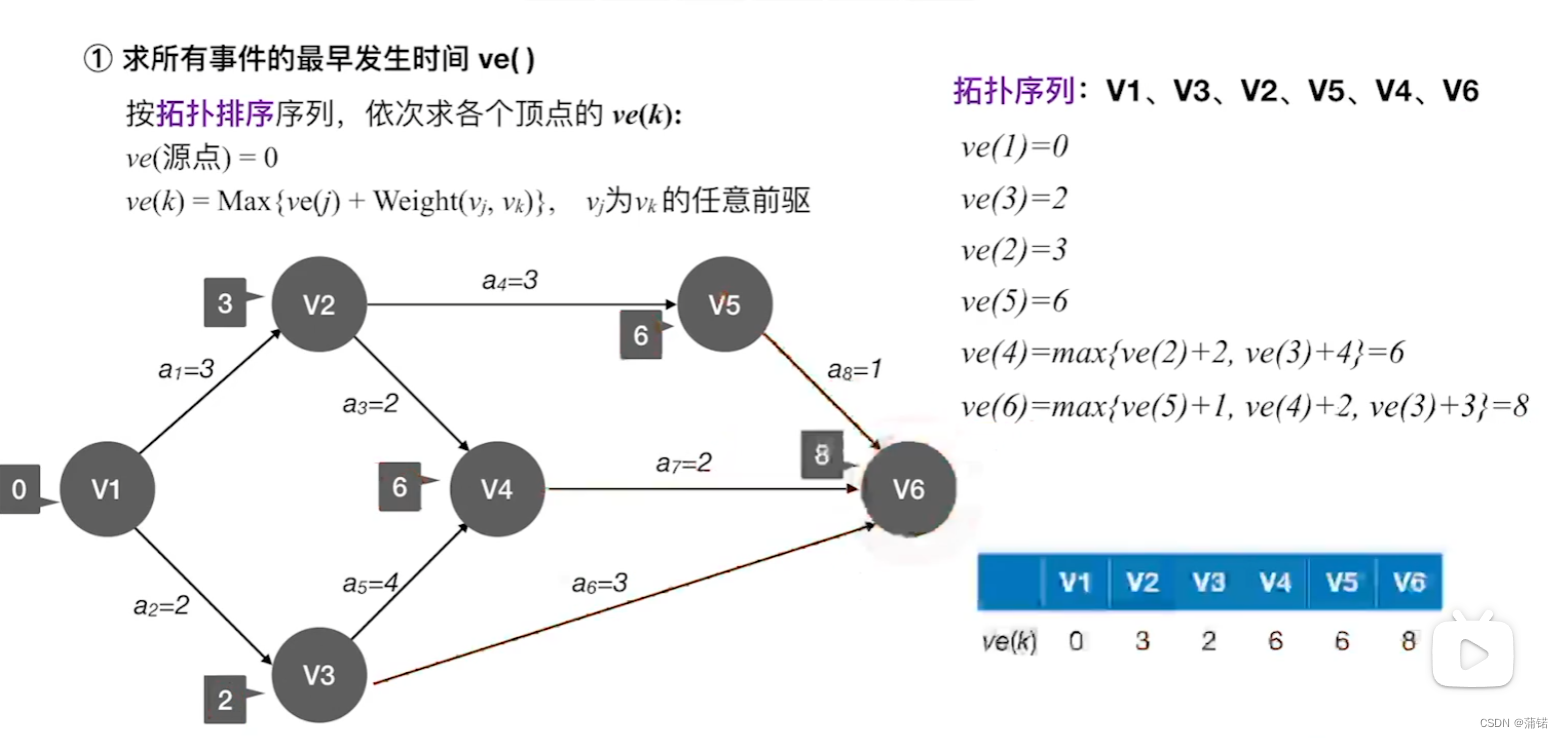
事件的最早发生时间Ve[k]
弧头指向自己,去看弧尾们结点的VE+边的权重中最大的,作为自己的VE
活动的最早开始时间E[i]
看边的弧尾是谁,其VE就是。
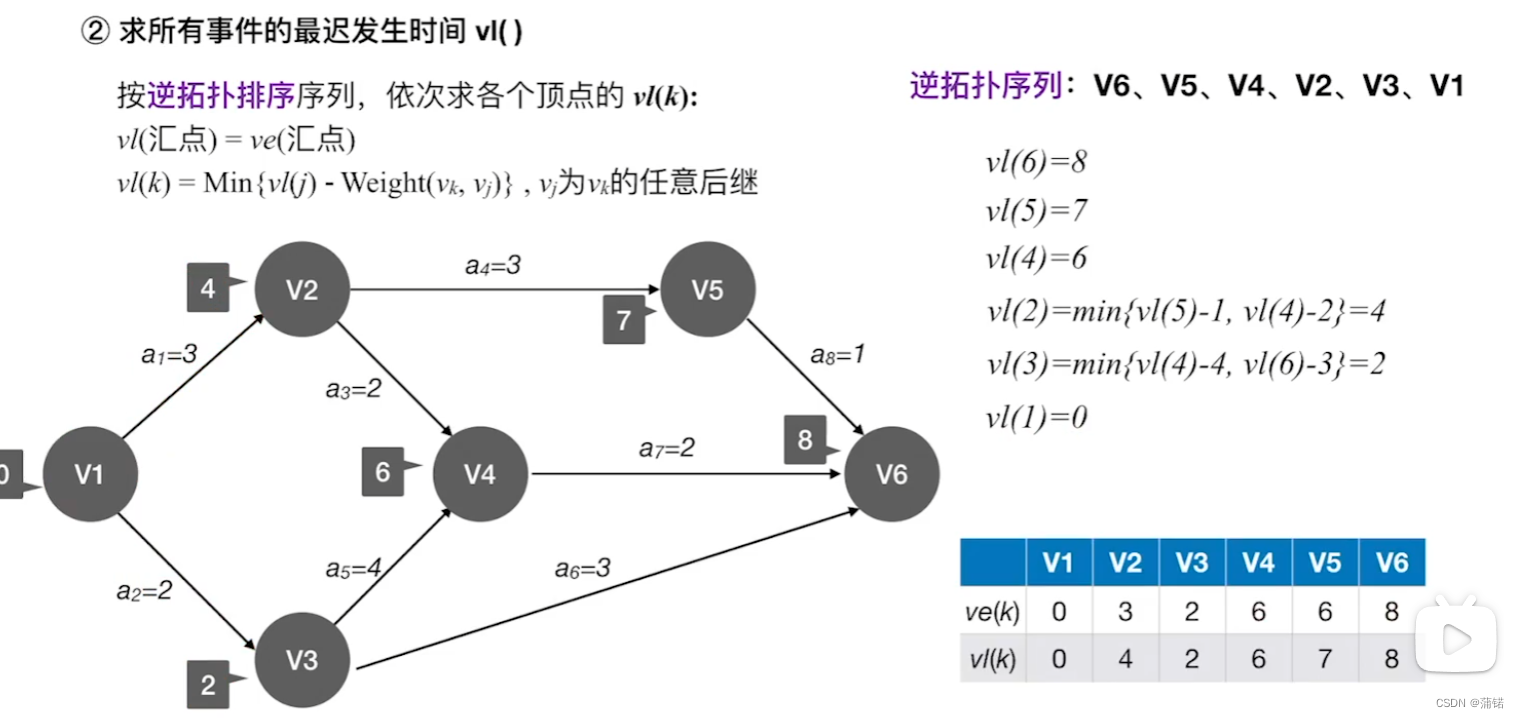
事件的最迟发生时间Vl[k]
自己作为弧尾,看弧头指向的结点的VL-边权 里面的最小值
活动的最晚开始时间L[i]
边的弧头VL - 权重
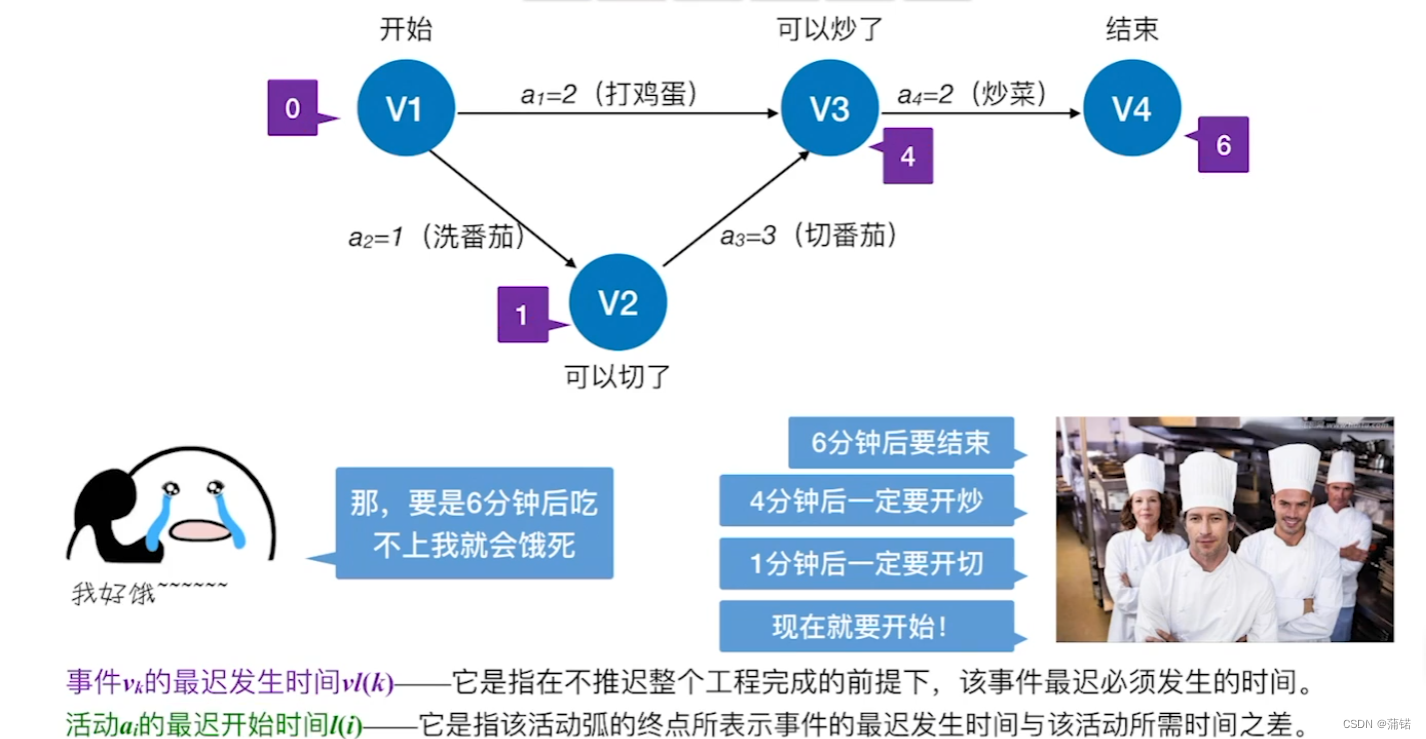
活动的时间余量
就是L-E
关于关键路径的缩短
若关键活动耗时增加,则整个工程的工期将增长
缩短关键活动的时间,可以缩短整个工程的工期
当缩短到一定程度时,关键活动可能会变成非关键活动
可能有多条关键路径,只提高一条关键路径上的关键活动速度并不能缩短整个工程的工期,只有加快那些包括在所有关键路径上的关键活动才能达到缩短工期的目的。
代码实现思路
- 对于代码实现,虽然说是邻接表存储(其实可以不用我感觉),不过要先拓扑排序得到拓扑序列。
- 然后取第一个源点,VE[i]设置为0,然后往后遍历拓扑序列,依次设置VE的值,就是edges[from][to],直到INF。
- 下一个,直接遍历从自己往后的拓扑序列,依次设置VE的值(注意这个过程中要Math.max(现在的edges[from][to],原先的值))。
- 如此直到终点
- 然后有了终点的VE之后,刚才的拓扑排序结果翻个过就行(然后到这,我意识到倒着没法用邻接表,于是干脆不用,把前面也改了,直接遍历逆拓扑序列,虽然有点出入,但能保证是邻接结点,然后碰到INF就结束)。
- 终点还是设置为VL=VE,然后遍历逆拓扑序列,弧头结点VL减去权重,就是弧尾结点的VL(注意这个过程中要Math.min(现在的edges[to][from]-weight,原先的)),直到INF。
- 在存入有向图时候,我们就可以用from to结构来存储边,然后根据已经有的VE和VL,我们先来存E,就是遍历,看它的from是谁,直接设置VE[from]就可以。
- 然后存L,就是遍历,看它的to是谁,直接设置VL[to]-weight就可以。
后续的代码,感觉用的不多,回头写了再上传上来吧,咕咕咕。