目录：

1： 常见函数的导数

2: 梯度与微分的关系

3: 常见函数的梯度

4： 梯度更新常见问题

---

一 常见函数的导数

（复合函数求导证明）

---

二 梯度与微分的关系

2.1 微分

： x 为一元变量时微分

： x 为向量时微分

矩阵

2.2 微分与梯度关系

1 根据给定的f 求微分 df

2 求df 的迹

3 等式右边简化到dx,可以得到对应的梯度

---

三 常见函数的梯度

3.1 已知 ,

则：

3.2 已知

则：

3.3 已知

则：

3.4 已知

则：

3.5 已知

则：

---

四 梯度的常见问题

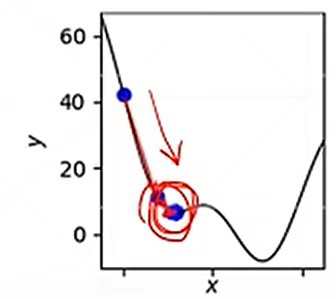
2.1 learing rate

过大的学习率，导致权重系数无法收敛.

理想的参数更新为绿色方向，到达极小值点

但是当学习率过大的时候,会导致参数更新如红色

方向,参数震荡

2.2 初始化值

相对于A点,B 点更容易陷入局部极小值点

2.3 动量

梯度不仅仅由当前的梯度决定，也由历史梯度叠加而成。

这样不会陷入到局部极小值点无法出来.