还记得当时才大一，上离散数学课，当时觉得很不屑，就是觉得这学的什么玩弄啥用没有，但是其实很多的算法思想在解决题目时很有价值。
本文就将使用染色法解决判断二分图问题，使用广度优先搜索遍历和 Java 语言实现

一、题目描述

存在一个 无向图 ，图中有 n 个节点。其中每个节点都有一个介于 0 到 n - 1 之间的唯一编号。给你一个二维数组 graph ，其中 graph[u] 是一个节点数组，由节点 u 的邻接节点组成。形式上，对于 graph[u] 中的每个 v ，都存在一条位于节点 u 和节点 v 之间的无向边。该无向图同时具有以下属性：

• 不存在自环（graph[u] 不包含 u）。
• 不存在平行边（graph[u] 不包含重复值）。
• 如果 v 在 graph[u] 内，那么 u 也应该在 graph[v] 内（该图是无向图）
• 这个图可能不是连通图，也就是说两个节点 u 和 v 之间可能不存在一条连通彼此的路径。

二分图定义：如果能将一个图的节点集合分割成两个独立的子集 A 和 B ，并使图中的每一条边的两个节点一个来自 A 集合，一个来自 B 集合，就将这个图称为 二分图 。

如果图是二分图，返回 true ；否则，返回 false 。

示例：

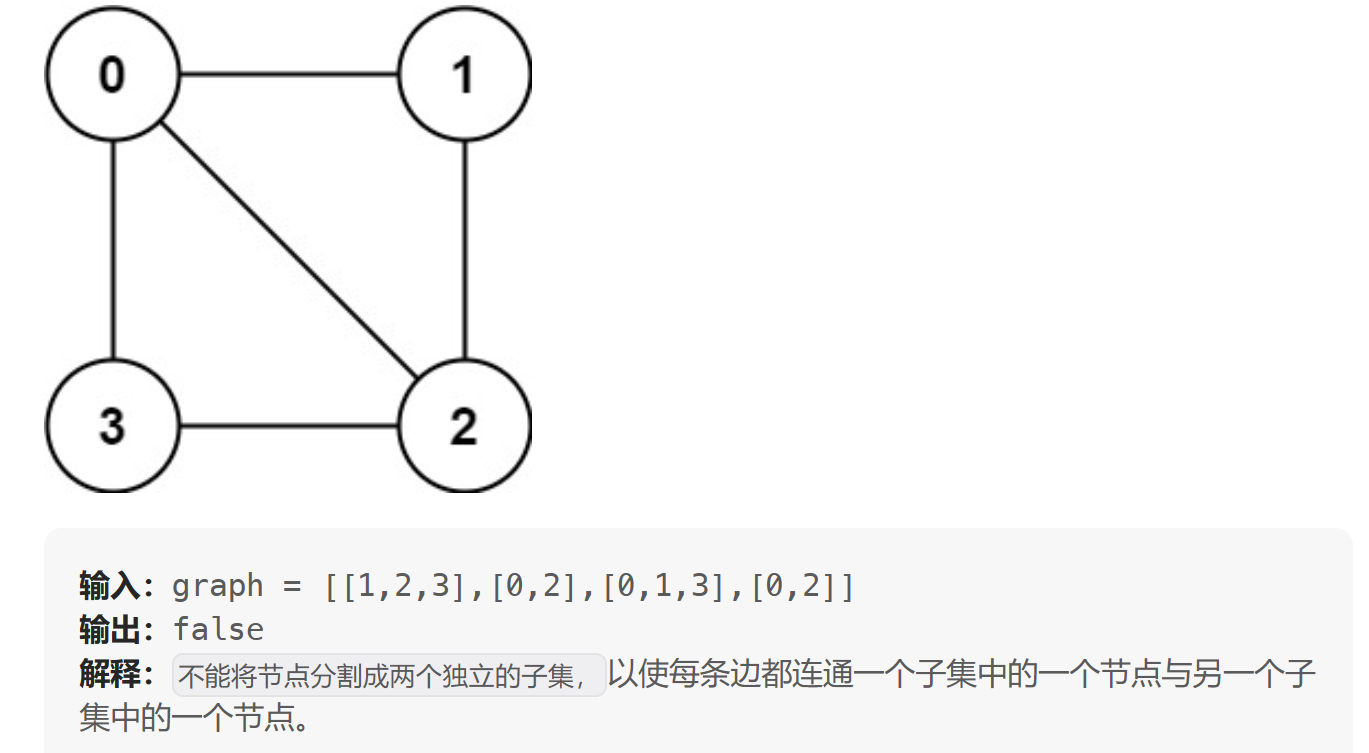
二、思路

1. 染色法思路：

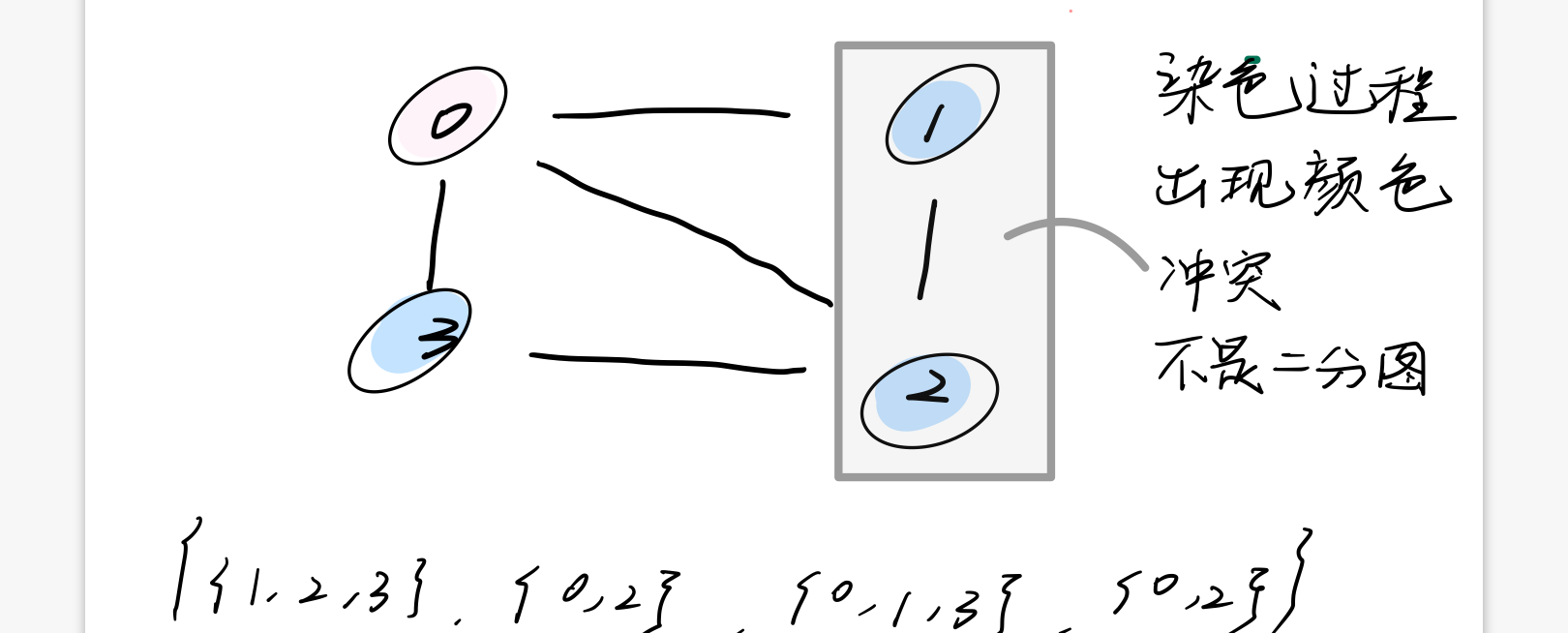
使用两种颜色对图中每个节点染色，对遍历到的节点染成一种颜色，将其相邻节点染成与其相反的颜色。

• 在染色的过程中，若出现了颜色冲突，则不是二分图
• 若一直未出现颜色冲突，则证明是二分图

代码实现 ——

这部分的代码实现思路很简单，我们可以额外引入一 visited[] 数组，0表示未访问过，1表示粉色，-1表示蓝色。

在遍历过程中，通过对 visited[] 数组的判断，判断颜色是否出现了冲突。

2. 广度优先搜索遍历思路

广度优先，顾名思义，对每个节点，搜索其所有相邻节点，在对这些相邻节点，搜索其下一层节点，周而复始，直到结束。

代码实现 ——

广度优先搜索遍历的代码实现上，就是个套路，与二叉树层次遍历类似，都是采用一个队列存储当前层的节点，遍历直至队列为空。

三、代码

    public boolean isBipartite(int[][] graph) {
        // 第一步 —— 定义 visit 数组， 0 表示当前节点未被访问过，1 表示染成粉色，-1 表示染成蓝色
        int[] visited = new int[graph.length];
        // 队列 —— 用于广度优先搜索遍历
        Queue<Integer> queue = new LinkedList<>();
        // 开始搜索
        for(int i=0; i<graph.length; i++){
            if(visited[i] != 0){ // 当前节点已经被访问过
                continue;
            }
            // 当前节点入队
            queue.offer(i);
            // 染成粉色
            visited[i] = 1;
            // 遍历当前层的所有节点
            while(!queue.isEmpty()){
                int temp = queue.poll();
                // 遍历当前节点的所有相邻节点
                for(int next : graph[temp]){
                    if(visited[next] == visited[temp]){ // 染色时，出现颜色冲突
                        return false;
                    }
                    if(visited[next] == 0){ // 当前邻节点未被染色过
                        visited[next] = -visited[temp]; // 染成相反颜色
                        queue.offer(next); // 加入队列
                    }
                }
            }
        }
        return true;
    }