一二叉查找树简介

二叉查找树【二叉搜索树或是二叉排序树】
- 左子树中所有结点的值，均小于其根结点的值
- 右子树中所有结点的值，均大于其根结点的值
- 二叉搜索树的子树也是二叉搜索树
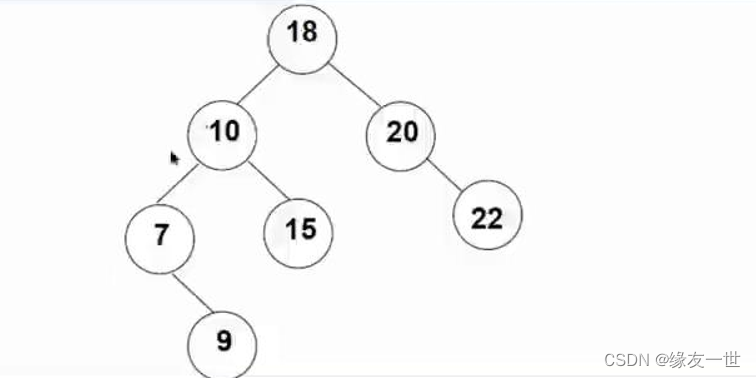
规则：二义查找树满足左边一定比当前结点小，右边一定比当前结点大
比如需要在这颗树种查找值为15的结点
1. 从根结点18开始，因为15小于18，所以从左边开始找
2. 接着来到10，发现10比15小，所以继续往右边走
3. 来到15，成功找到。

二创建和插入操作

结点的结构和二叉搜索树的创建

#include<iostream>
using namespace std;
typedef int E;
typedef struct TreeNode {
    E element;
    struct TreeNode *left;
    struct TreeNode *right;
} *Node;

Node createNode(E element) {
    Node node = (Node) malloc(sizeof(struct TreeNode));
    node->left = node->right = NULL;
    node->element = element;
    return node;
}

插入

二叉树不能插入重复元素，如果出现重复元素，则直接忽略
关于代码实现部分，如果对递归不太熟悉的朋友可以运行完整代码进行调试，逐步进行有利于理解程序的运行！

Node insert(Node root,E element) {
    if(root) {
        if(element< root->element)
            root->left= insert(root->left,element);
        else if(element>root->element)
            root->right= insert(root->right,element);
    }else {//当节点为空时，说明已经找到插入的位置，创建对应的结点
        root= createNode(element);
    }
    return root;//返回当前结点
}

三查找操作

3.1 查找思路

查找的思路就是不断比较值的大小，直到找到数值
如果要查找最大值，就不断往右边遍历；如果要查找最小值，就不断往左边遍历。

3.2 代码实现

Node find(Node root,E target) {
    while(root) {
        //如果要找的值比当前值小，就往左边查找
        //如果要找的值比当前值大，就往右边查找
        //否则，就是找到了
        if(target<root->element) {
            root=root->left;
        }else if(target>root->element) {
            root=root->right;
        }else {
            return root;
        }
    }
    //如果没找到，就返回NULL
    return NULL;
}
Node findMax(Node root) {
    while(root && root->right) {
        root=root->right;
    }
    return root;
}

四删除操作

4.1 情况讨论

首先分析一下，删除操作可能出现的情况
1. 要删除的结点是叶子节点
2. 要删除的结点只有一个孩子结点
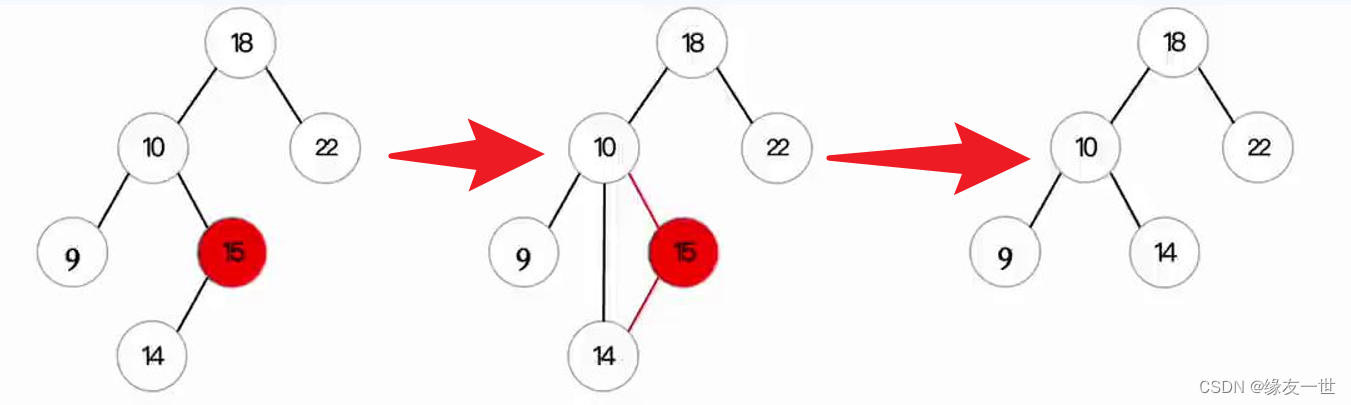
3. 要删除的结点有两个孩子结点
  - 为保持二叉查找数的性质，我们需要选择一个孩子补充删除的结点。这里选取其左子树中最大节点上位

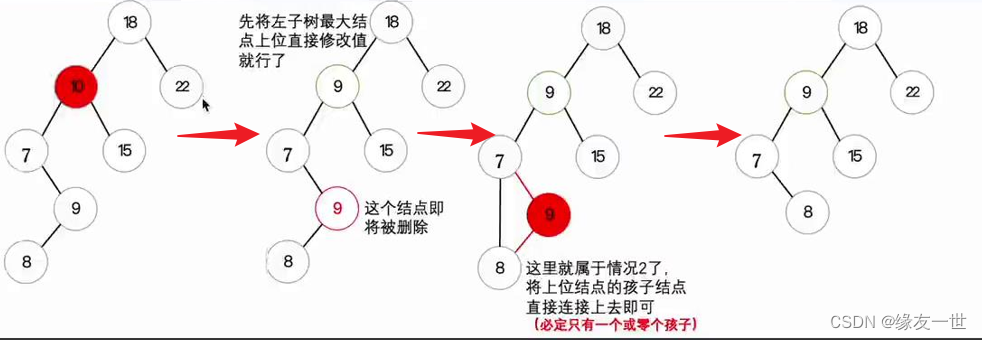
在这里插入图片描述

4.2 代码实现

Node deleteValue(Node root,E target) {
    if(root==NULL) return NULL;
    if(target<root->element) {
        root->left= deleteValue(root->left,target);
    }else if(target>root->element) {
        root->right= deleteValue(root->right,target);
    }else {//找到的情况
        //处理结点左右都有孩子的情况
        if(root->left && root->right) {
            //第一步：找到左边最大的值
            Node leftMax= findMax(root->left);
            //第二步：将原来的值替换为其左子树的最大值
            root->element=leftMax->element;
            //第三步：删除最大值【只有一个左孩子或者没孩子】,返回删除结点的根节点
            //同时注意的是：将情况转化为删除只有一个孩子\叶子结点的情况
            //函数会进入下面的情况[else]中进行处理
            root->left= deleteValue(root->left,root->element);
        }else {
            //只要删除这个节点，
            //当这个节点有走孩子或右孩子时，就进行删除孩子结点并修改指针指向；否则，直接删除当前节点即可
            Node temp=root;
            if(root->right) {
                root=root->right;
            }
            else {
                root=root->left;
            }
            free(temp);
        }
    }
    return root;//返回最终的结点
}

五完整代码

作者在这里列出完整的代码，并不希望诸位直接粘贴复制
希望诸位可以在运行代码调试的过程中，加深对这部分内容的理解。
删除操作部分的代码涉及到递归且情况较为复杂，读者可以运行这儿的代码，认真理解删除的具体实现！

5.1 二叉查找树的结构

5.2 完整代码内容

//
// Created by HP on 2023/1/10.
//

#include<iostream>
using namespace std;
typedef int E;
typedef struct TreeNode {
    E element;
    struct TreeNode *left;
    struct TreeNode *right;
} *Node;

Node createNode(E element) {
    Node node = (Node) malloc(sizeof(struct TreeNode));
    node->left = node->right = NULL;
    node->element = element;
    return node;
}

Node insert(Node root,E element) {
    if(root) {
        if(element< root->element)
            root->left= insert(root->left,element);
        else if(element>root->element)
            root->right= insert(root->right,element);
    }else {//当节点为空时，说明已经找到插入的位置，创建对应的结点
        root= createNode(element);
    }
    return root;//返回当前结点
}

void inOrder(Node root) {
    if(root==NULL) return ;
    inOrder(root->left);
    cout<<root->element<<" ";
    inOrder(root->right);
}

Node find(Node root,E target) {
    while(root) {
        //如果要找的值比当前值小，就往左边查找
        //如果要找的值比当前值大，就往右边查找
        //否则，就是找到了
        if(target<root->element) {
            root=root->left;
        }else if(target>root->element) {
            root=root->right;
        }else {
            return root;
        }
    }
    //如果没找到，就返回NULL
    return NULL;
}
Node findMax(Node root) {
    while(root && root->right) {
        root=root->right;
    }
    return root;
}
Node deleteValue(Node root,E target) {
    if(root==NULL) return NULL;
    if(target<root->element) {
        root->left= deleteValue(root->left,target);
    }else if(target>root->element) {
        root->right= deleteValue(root->right,target);
    }else {//找到的情况
        //处理结点左右都有孩子的情况
        if(root->left && root->right) {
            //第一步：找到左边最大的值
            Node leftMax= findMax(root->left);
            //第二步：将原来的值替换为其左子树的最大值
            root->element=leftMax->element;
            //第三步：删除最大值【只有一个左孩子或者没孩子】,返回删除结点的根节点
            //同时注意的是：将情况转化为删除只有一个孩子\叶子结点的情况
            //函数会进入下面的情况[else]中进行处理
            root->left= deleteValue(root->left,root->element);
        }else {
            //只要删除这个节点，
            //当这个节点有走孩子或右孩子时，就进行删除孩子结点并修改指针指向；否则，直接删除当前节点即可
            Node temp=root;
            if(root->right) {
                root=root->right;
            }
            else {
                root=root->left;
            }
            free(temp);
        }
    }
    return root;//返回最终的结点
}
int main() {
    Node root= insert(NULL,18);
    insert(root,22);
    insert(root,10);
    insert(root,7);
    insert(root,15);
    insert(root,9);
    insert(root,8);
    inOrder(root);
    cout<<endl;
    Node res=find(root,17);
    if(res)
        cout<<res->element<<endl;
    else
        cout<<"没找到"<<17<<endl;
    Node res1=find(root,9);
    if(res1)
        cout<<res1->element<<endl;
    else
        cout<<"没找到"<<endl;
    cout<<"成功删除："<<deleteValue(root,10)->element;
    return 0;
}