Hermite多项式

Hermite多项式是一种非常重要的正交多项式，尤其在量子力学中，是谐振子的本征态，在物理学中，其定义为

$$H_n(x)=(-1{)}^n{e}^{x^2}\frac{{\text{d}}^n}{\text{d}{x}^n}{e}^{-x^2}$$

其中$n$为厄密特多项式的阶数，在Python中，提供了Hermite类，构造函数为

numpy.polynomial.hermite.Hermite(coef, domain=None, window=None, symbol='x')

其中coef为系数列表$a_0,a_1,\cdots ,a_n$，表示生成

$$\sum _{i=0}^n{a}_i{H}_i(x)$$

domain表示$x$的定义域，window表示缩放系数。

from numpy.polynomial.hermite import Hermite
h3 = Hermite(coef=[4,3,2,1])
print(h3)
# 输出为4.0 + 3.0 H_1(x) + 2.0 H_2(x) + 1.0 H_3(x)

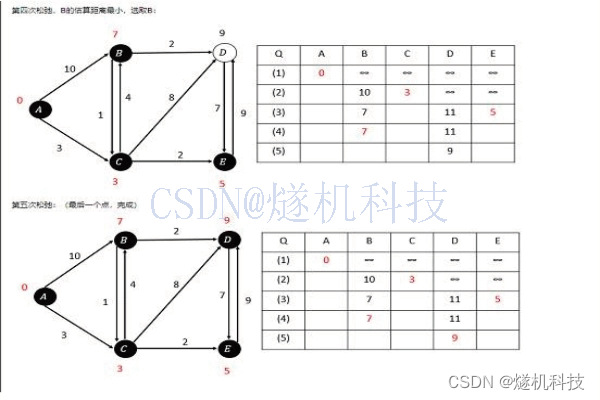
为了便于理解Hermite多项式到底是个啥，可以绘制一下不同阶数的Hermite多项式的函数

import matplotlib.pyplot as plt
for i in range(5):
    c = np.zeros(i+1)
    c[i] = 1
    h = Hermite(coef=c, domain=(-5,5))
    xs, ys = h.linspace()
    plt.plot(xs, ys, label=str(i))

plt.legend()
plt.show()

其中h.linspace表示在定义域范围内对多项式进行采样，有一个参数n，表示在定义域范围内等间隔生成n组$x,y$，默认为100。

得图如下

求导和积分

Hermite支持简单的符号计算，比如可通过deriv(n)求多项式的n阶导数；通过integ(n)可求n阶积分，示例如下

>>> h3.deriv(1)
Hermite([6., 8., 6.], domain=[-1.,  1.], window=[-1.,  1.])
>>> h3.deriv(3)
Hermite([48.], domain=[-1.,  1.], window=[-1.,  1.])
>>> h3.integ(2)
Hermite([0.5       , 0.        , 0.5       , 0.125     , 0.04166667, 0.0125    ], domain=[-1.,  1.], window=[-1.,  1.])

求导后得到的系数可通过递推关系验证，

$$H_n^{\prime }(x)=2n{H}_{n-1}(x)$$

所以$H_3^{\prime }(x)=6H_2^{\prime }(x)$，即上述计算是没毛病的。

求根和反演

roots可用于求根，而fromroot可根据根来生成Hermite多项式

rs = h3.roots()
print(rs)
# [-1.50000000e+00, -3.61717794e-16,  5.00000000e-01]
pNew = p3.fromroots(rs)
print(pNew)
# 0.49999999999999983 + 0.37499999999999994 H_1(x) +
# 0.25000000000000006 H_2(x) + 0.125 H_3(x)

可以发现roots和fromroots并非对称的关系。

拟合

Hermite类中同样提供了拟合函数fit，定义为

Hermite.fit(x, y, deg, domain=None, rcond=None, full=False, w=None, window=None, symbol='x')

其中domain, window, symbol不必赘述，其中x,y为待拟合多项式；deg为多项式的阶数。rcond表示截止误差。full为False时，只返回拟合系数，否则还返回拟合的标准差等。

>>> p3.fit(xs, ys, 3)
>>> xs, ys = h3.linspace()
>>> h3_3 = h3.fit(xs, ys, 3)
>>> print(h3_3)
3.999999999999998 + 3.000000000000002 H_1(x) + 1.9999999999999984 H_2(x) +
1.0000000000000002 H_3(x)
>>> h3_4 = h3.fit(xs, ys, 4)
>>> print(h3_4)
3.9999999999999916 + 3.0000000000000036 H_1(x) +
1.9999999999999896 H_2(x) + 1.0000000000000002 H_3(x) -
9.797539357718845e-16 H_4(x)

可见其拟合效果还是不错的。

其他

degree返回多项式的最高项次数，cutdeg可以对多项式的次数做阶段，例如

>>> h3.degree()
3
>>> h3.cutdeg(2)
Hermite([4., 3., 2.], domain=[-1.,  1.], window=[-1.,  1.])