文章目录
- 简介
- 常见的Big-Oh
简介
精确的考虑程序运行时间会使得寸步难行,而且毫无意义,所以可以用一种“概量”的概念来衡量运行时间,称之为“时间复杂度”。
时间复杂度的定义:
在一个完全立项状态下的计算机中,我们定义T(n)来表示程序执行所要花费的时间,其中n代表数据的输入量。当人程序的最坏运行时间或最大运行时间是时间复杂度的衡量标准,一般以Big-Oh表示
在分析算法的时间复杂度时,往往用函数来表示它的成长率(Rate of Growth),其实时间复杂度是一种“渐进表示法”
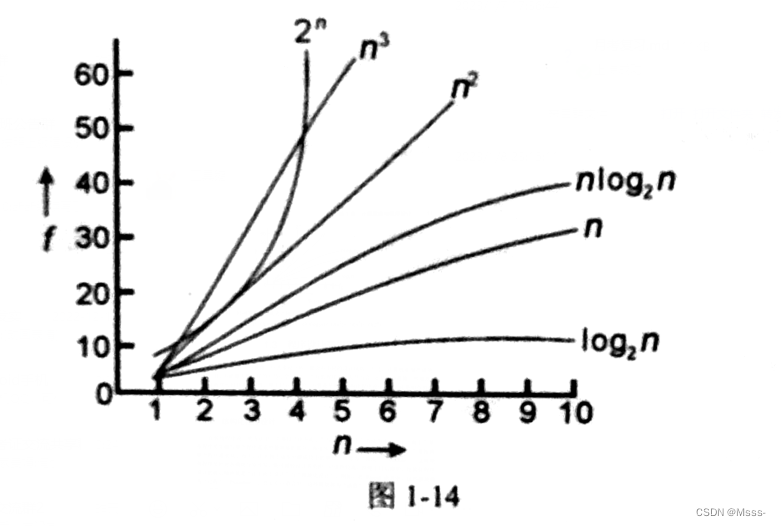
常见的Big-Oh
| Big-Oh | 特色与说明 |
|---|---|
| O(1) | 称为常数时间,表示算法的运行时间是一个常数倍 |
| O(n) | 称为线性时间,表示执行的时间会随着数据集合的大小而线性增长 |
| O( l o g 2 log_2 log2n) | 称为次线性时间,成长速度比线性时间慢,而比常数时间快。 |
| O( n 2 n^2 n2) | 称为平方时间,算法的运行时间会成二次方的增长 |
| O( n 3 n^3 n3) | 称为立方时间,算法的运行时间会成三次方增长 |
| O( 2 n 2^n 2n) | 称为指数时间,算法的运行时间会成2的n次方增长。 |
| O(n l o g 2 log_2 log2n) | 称为线性乘对数时间,介于线性和二次方增长的中间模式 |
大佬博文:
如何计算时间复杂度
时间复杂度怎么计算?