查询中位数

给定线性序集中n个元素和一个整数k 【k=(n+1)/2】，要求找出这n个元素中第k小的元素，即找中位数。线性序列没有排序,没有重复值。

已知快速排序划分时一个划分基准数的位置在确定后，在之后排序中是不会变的。利用此特性，以下算法模仿快速排序，但只对划分出的子数组之一进行处理，时间复杂度为O(n)，比排序完查找更快。

如果n=0或1，不需要找（唯一一个数据就是要找的）

如果当前基准数不是所求的，在相应的子串中找（相当于快排中划分好了的三段）

---

查询中位数将k设为n/2。以下可以查询第k小的任何一个数。

由于使用分治策略，这里的k是在子串中相对的第k小（k是相对left和right的位置），但是划分函数返回的下标mid是绝对位置，所以，可以用一个变量（j）存储mid在子串中的相对位置。

SelectK每一次递归时left和right也会发生变化，相应的k也要注意改变（k-j）。

int SelectK(int* nums, int left, int right, int k)
{
    if (left == right&&k==1)//剩下一个元素找里面第一小的元素
        return nums[left];
    int mid = Partition(nums, left, right);
    int j = mid + 1 - left;//j是相对在子串中的位置（第j个）
    if (k <= j)return SelectK(nums, left, mid, k);
    else return SelectK(nums, mid + 1, right, k-j);
}
int SelectKMin(int* nums, int n, int k)
{
    if (nullptr == nums || n < 1 || k<1 || k>n)
        return -1;
    return SelectK(nums, 0, n - 1, k);
}

划分函数

同快排的划分

int Partition(int*nums,int left,int right)
{
    int tmp = nums[left];
    while (left < right)
    {
        while (left<right && nums[right]>tmp)right--;
        if(left<right)nums[left] = nums[right];
        while (left < right && nums[left] < tmp)left++;
        if (left < right)nums[right] = nums[left];
    }
    nums[left] = tmp;
    return left;
}

测试

int main()
{
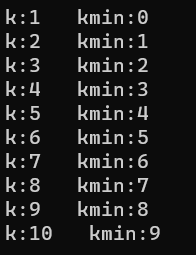
    int a[] = { 5,3,6,7,9,8,4,2,1,0 };
    int n = sizeof(a) / sizeof(a[0]);
    int k = 0;
    for (k = 1; k <= n; k++)
    {
        int kmin = SelectKMin(a, n, k);
        printf("k:%d   kmin:%d\n", k, kmin);
    }
}

一维最接近点对

给定一维线上n个点，找其中的一对点，使得在n个点组成的所有点对中，该点对的距离最小。如果有多于一对只找1对作为解。

如果暴力求解每一对之间的距离需要O(n^2)太慢了。将每个点的位置存在数组中，利用分治法：

将数组划分后产生两个子集合，差值最小有三个部位可能产生：

当集合中元素个数<2时，无法计算差值，此时应返回INT_MAX

设左边集合为S1，最小差为d1；右边集合为S2，最小差d2；S2中最小值q和S1最大值p相减得的差，三个数相比最小的值即为最接近点对的差值。

为了将数组平分减少计算次数，需要找中位数并用其作为划分基准。

主要代码：

int CpairNum(int* nums, int left, int right)
{
    if ((right - left) < 1)return INT_MAX;//少于两个数没有差值
    int m = (right - left + 1) / 2;//当前数组中位数的位置（left~right）
    int pos = left + m - 1;//绝对位置（0~n-1）
    SelectK(nums, left, right, m);//找中位数的值，然后划分成左右两个数组
    int d1 = CpairNum(nums, left,pos);//S1继续递归
    int d2 = CpairNum(nums,pos+1 ,right );//S2继续递归
    int p = MaxS1(nums, left ,pos);//S1中最大的元素
    int q = MinS2(nums,pos+1, right);//S2中最小的元素
    return Min3(d1, d2, q - p);//对比找到最小元素
}
int Cpair(int* nums, int n)
{
    if (n < 2 || nums == nullptr)return INT_MAX;
    return CpairNum(nums, 0, n - 1);
}

其余代码：

//划分函数
int Partition(int* nums, int left, int right)
{
    int tmp = nums[left];
    while (left < right)
    {
        while (left<right && nums[right]>tmp)right--;
        if (left < right)nums[left] = nums[right];
        while (left < right && nums[left] < tmp)left++;
        if (left < right)nums[right] = nums[left];
    }
    nums[left] = tmp;
    return left;
}
//找第k小元素下标
int SelectK(int* nums, int left, int right, int k)
{
    if (left == right && k == 1)
        return nums[left];
    int mid = Partition(nums, left, right);
    int j = mid - left + 1;
    if (k == j)return nums[mid];
    if (k <j)return SelectK(nums, left, mid, k);
    else return SelectK(nums, mid + 1, right, k - j);
}
//S1里面最大的
int MaxS1(int*nums,int left ,int right)
{
    return nums[left];
}
//S2里面最大的
int  MinS2(int *nums,int left,int right)
{
    int min = INT_MAX;
    for (int i = left; i <= right; i++)
    {
        if (nums[i] < min)
        {
            min = nums[i];
        }
    }
    return min;
}
//三个最小差里面最小的
int Min(int a, int b)
{
    return a < b ? a : b;
}
int Min3(int a, int b, int c)
{
    return Min(a, Min(b, c));
}

排好序再计算的方法无法直接推广到二维的情形，而分治法求解可以。